Уравнение изменения импульса механической системы.

Первый закон Ньютона

Первый закон Ньютона (закон инерции): существуют такие системы отсчета, относительно которых тело при отсутствии на неe внешних воздействий сохраняет состояние покоя или равномерного прямолинейного движения.

Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно.

Система отсчета, связанная с поездом, идущим с постоянной скоростью по прямолинейному участку пути, – тоже инерциальная система (приближенно)Ускорения какого-либо тела в разных инерциальных системах одинаковы.
Наблюдения показывают, что с очень высокой степенью точности можно считать инерциальной системой отсчета гелиоцентрическую систему, у которой начало координат связано с Солнцем, а оси направлены на определенные «неподвижные» звезды.

С гораздо большей точностью можно считать инерциальной систему отсчета, в которой начало координат совмещено с центром Солнца, а координатные оси направлены к неподвижным звездам. Эту систему отсчета называют гелиоцентрической. Инерциальными являются и системы отсчета, которые движутся равномерно и прямолинейно относительно какой-либо инерциальной системы отсчета.

Галилей установил, что никакими механическими опытами, поставленными внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется равномерно и прямолинейно. Это утверждение носит название принципа относительности Галилея или механического принципа относительности.

Второй закон Ньютона

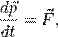Второй закон описывает, что происходит с физическим телом под воздействием внешних сил. Чем больше сумма приложенных к телу внешних сил, тем большее ускорение приобретает тело. Одновременно, чем массивнее тело, к которому приложена равная сумма внешних сил, тем меньшее ускорение оно приобретает. В математическом виде они записываются так: F = ma

Формулировка второго закона Ньютона с использованием понятия импульса:

Третий закон Ньютона

Закон этот гласит, что если тело А воздействует с некоей силой на тело В, то тело В также воздействует на тело А с равной по величине и противоположной по направлению силой. Иными словами, стоя на полу, вы воздействуете на пол с силой, пропорциональной массе вашего тела.

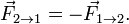Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

3)

Центр масс механичиской системы - воображаемая точка С, расположение которой характеризует распределение масс в системе. Центр масс механической системы движется, как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все силы действующие на систему.

Закон движения центра масс.

Воспользовавшись законом изменения импульса, получим закон движения центра масс:

dP/dt = M∙dV_c/dt = ΣF_i

Центр масс системы движется так же, как двигалась бы частица с массой, равной массе системы, под действием силы, равной векторной сумме всех внешних сил, действующих на входящие в систему частицы.В частности, центр масс замкнутой системы относительно произвольной ИСО движется равномерно прямолинейно или покоится. Изменение импульса центра масс происходит за счет внешних сил. Внутренние силы не влияют на характер его движения, если внешнее воздействие на систему постоянно и однородно

Если внешнее воздействие изменяется, то на различные части системы начинают действовать разные силы и характер движения центра масс меняется

Закон сохранения импульса.

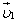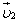Обозначим скорости тел массами m₁ и m₂ до взаимодействия через и , а после взаимодействия — через 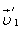и .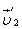

По третьему закону Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому их можно обозначить 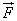и .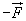

Для изменений импульсов тел при их взаимодействии на основании равенства (16.2)с можно записать

,

,

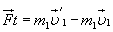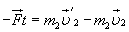где t — время взаимодействия тел. Из этих выражений получаем

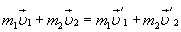. (16.3)

Таким образом, векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия.

Система тел, не взаимодействующих с другими телами, не входящими в эту систему, называется замкнутой системой.

Центральные силы

Центральные силы, приложенные к телу силы, линии действия которых при любом положении тела проходят через одну и ту же точку, называемую центром сил. а действующие в нем силы – центральными (например, гравитационные, кулоновские, упругие).

Центральные силы являются консервативными. Здесь работа зависит от характера взаимодействия и от начальных и конечных расстояний между частицами.

7)

Потенциальная энергия — механическая энергия системы тел, определяемая их вза­имным расположением и характером сил взаимодействия между ними. Способность совершить работу за счет любых других свойств тела

Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, — консервативными.

Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести 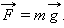Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения 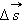на ось OY, направленную вертикально вверх:

ΔA = Fт Δs cos α = –mgΔs y,

где F_т = F_тy = –mg – проекция силы тяжести, Δs_y – проекция вектора перемещения. При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δs_y > 0. Если тело переместилось из точки, расположенной на высоте h₁, в точку, расположенную на высоте h₂ от начала координатной оси OY ,то сила тяжести совершила работу

A = –mg (h2 – h1) = –(mgh2 – mgh1).

Эта работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести

Eр = mgh.

Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.

Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.

A = –(Eр2 – Eр1).

Потенциальная энергия гравитационного взаимодействия

Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами т и М, находящихся на расстоянии r одна от другой, равна

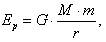(11)

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е_p = 0) принят при r = ∞. Потенциальная энергия гравитационного взаимодействия тела массой т с Землей, где h – высота тела над поверхностью Земли, М₃ – масса Земли, R₃ – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.

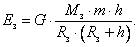(12)

При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой т с Землей для малых высот h (h « R₃) равна

Е_p = m∙g∙h,

Потенциальная энергия взаимодействия двух точечных зарядов равна W_пот=kq₁q₂/r

8)

Полная механическая энергия системы - это сумма её кинетической и потенциальной энергией: E = Eк + Eп. Её вид может выглядеть так: E = (mv^2)/2 + mgh (для случая свободного падения тела). По закону сохранения энергии, эта сумма всегда остаётся неизменной, если, конечно, часть энергии не будет отводиться во внутреннюю, но это уже - не механическая, а тепловая энергия. Полная механическая энергия определяется именно суммой Eк + Eп, её изменение связано с переходом части механической энергией в энергию других физических взаимодействий. Если же такие взаимодействия не проявляются, то полная механическая энергия всегда сохраняется. Изменение кинетической энергии системы равно суммарной работе всех сил, действующих на тела этой системы

∆E_к = A_пот.с.+ A_{непот.с.}+ A_внеш.с.

Изменение потенциальной энергии системы равно работе потенциальных сил с обратным знаком :

∆E_п = - A_пот.с

Очевидно, что изменение полной механической энергии равно:

∆E = ∆E_п +∆Е_к

Из уравнений получим, что изменение полной механической энергии равно суммарной работе всех внешних сил и внутренних непотенциальных сил.
∆E_к = A_внеш.с.+ A_{непот.с.}

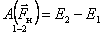Или
Мы пришли к следующему важному выводу:

Работа, совершаемая внешними неконсервативными силами при переходе системы из одного состояния в другое, равна изменению механической энергии системы.

Закон сохранения механической энергии :

Механическая энергия консервативной механической системы сохраняется во времени. Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может никуда исчезнуть.
Для замкнутой системы физических тел, например, справедливо равенство
E_k1 + E_p1 = E_k2 + E_p2,
где E_k1, E_p1 — кинетическая и потенциальная энергии системы какого-либо взаимодействия, E_k2, E_p2 — соответствующие энергии после.

10)

Момент импульса частицы:

Моментом импульса (количества движения)материальной точки Аотносительно неподвижной точки Оназывается физическая величина, определяемая векторным произ­ведением:

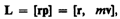
где r — радиус-вектор, проведенный из точки О в точку A, p=mv — импульс материальной точки

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдель­ная точка тела движется по окружности постоянного радиуса r_i с некоторой скоро­стью v_i . Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. с. радиус является плечом вектора m_iv_i . Поэтому можем записать, что момент импульса отдель­ной частицы равен

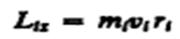
Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке.

Если известен радиус-вектор r⃗ точки приложения силы F⃗ относительно точки О, то момент этой силы относительно О выражается следующим образом:

M⃗ O(F⃗ )=r⃗ ×F⃗ .

Действительно, модуль этого векторного произведения:

|M⃗ O|=|r⃗ ×F⃗ |=|r⃗ ||F⃗ |sinα.

В соответствии с рисунком |r⃗ |sinα=h, поэтому:

|M⃗ O|=|F⃗ |h.

Момент силы считается положительным, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки и отрицательным, если по ходу часовой стрелки

Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия. Момент силы относительно центра О равен нулю, если сила равна нулю или, если линия действия силы проходит через центр О (плечо рав-но нулю). Графически абсолютная величина момента силы относительно центра О вы-ражается удвоенной площадью ОАВ

Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.

Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.
Поэтому ,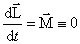

Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.

11)

Основное уравнение динамики вращательного движения твердого тела:

Второй закон Ньютона для вращательного движения

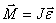
По определению угловое ускорение 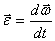и тогда это уравнение можно

переписать следующим образом

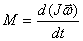
с учетом (5.9)

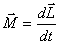
или

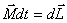(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела 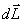, равно импульсу момента 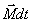всех внешних сил, действующих на это тело.

12)

Кинетическая энергияизмеряется работой, которую тело может произвести благодаря инерции при затормаживании тела до полной остановки.

При вращательном движении роль массы m выполняет момент инерции I, а вместо линейной скорости v выступает угловая скорость ω, и формула кинетической энергии при вращательном движении тела вокруг неподвижной оси приобретает вид:

,

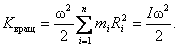(6.4.1)

Если тело вращается вокруг неподвижной оси z с угловой скоростью 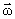, то линейная скорость i-й точки 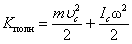, R_i – расстояние до оси вращения

Если произвольная м.т. вращается по окружности и на нее действует сила 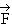,то при повороте на некоторый угол совершается элементарная работа dА = F ds, где ds=r dj. Тогда

dА =(r F) dj = M dj.

(5.18)

Полученное выражение остается справедливым и случае системы м.т., совершающих вращательное движение относительно оси z при w =сonst. В этом случае момент внутренних сил равен нулю и работа не совершается. Для нахождения полной работы необходимо вычислить интеграл

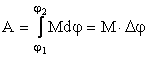
13)

Виды движения:

Имеется пять видов движения твердого тела:

1) Поступательное движение твёрдого тела - это такое его движение, при котором любая прямая, жёстко связанная с телом, перемещается, оставаясь параллельной своему

первоначальному направлению.

2)Вращательное движение твёрдого тела - это такое движение, при котором все его

точки движущиеся по окружностям, центры которых находятся вне пределов тела.

3) плоское, если все точки тела движутся в плоскостях, параллельных некоторой плоскости, неподвижной в рассматриваемой системе отсчета.

4)сферическое, если одна из точек тела остается все время неподвижной в рассматриваемой системе отсчета.

5)свободное, если нет перечисленных выше четырех ограничений.

Произвольное движение твердого тела складывается из поступательного движения и вращения. При равновесии для исключения возможности поступательного движения требуется равенство нулю суммы всех сил, а для исключения возможности вращения - равенство нулю суммы всех моментов.

Произвольное перемещение твердого тела из положения 1 в положение 2 можно представить как сумму двух перемещений — поступательного перемещения из положения в положение V или и поворота вокруг оси О или оси .Очевидно, что такое разбиение перемещения на поступательное и вращательное может быть осуществлено бесчисленным множеством способов, однако в любом случае производится поворот на один и тот же угол.

В соответствии со сказанным выше элементарное перемещение какой-либо точки тела можно разложить на два перемещения — «поступательное» и «вращательное»:

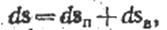
причем для всех точек тела одно и то же. Такое разложение перемещения можно, как мы видели, осуществить различными способами, причем в каждом случае вращательное перемещение осуществляется поворотом тела на один и тот же угол (но относительно различных осей), в то время как оказываются различными.

Разделив на соответствующий промежуток времена dt, получим скорость точки

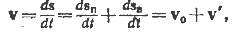
где v — одинаковая для всех точек тела скорость поступательного движения и v — различная для разных точек тела скорость, обусловленная вращением.

15)

16)

Уравнение гармонических колебаний

Уравнение (1)

Однако обычно под уравнением колебаний понимают иную запись этого уравнения, в дифференциальной форме. Возьмем для определенности уравнение (1) в виде

дважды продифференцируем его по времени:

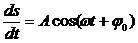
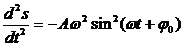
Видно, что выполняется следующее соотношение:

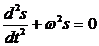⁽²⁾

которое и называется уравнением свободных гармонических колебаний (в дифференциальной форме). Уравнение (1) является решением дифференциального уравнения (2). Поскольку уравнение (2) - дифференциальное уравнение второго порядка, необходимы два начальных условия для получения полного решения

17)

Вынужденные механические колебания.Свободные колебания реальной колебательной системы являются затухающими. Чтобы колебания были незатухающими, необходимо компенсировать потери энергии, обусловленные силами сопротивления. Это можно сделать, воздействуя на систему (рис.27.3) внешней силой, изменяющейся по гармоническому закону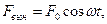

где 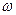- частота вынуждающей силы.

Уравнение движения запишется с учетом всех сил ( 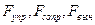) запишется в виде

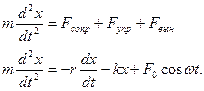
Поделив обе части на m и перенося первые два члена из правой части в левую, получим

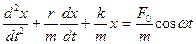
Обозначив, как и в п.6 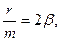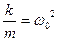, получим дифференциальное уравнение вынужденных колебаний 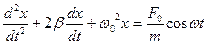(13)

Уравнение является неоднородным. Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения

.

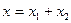Общее решение однородного уравнения (правая часть (13) равна нулю) нам уже известно

.

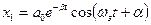Роль х1 уменьшается и по прошествии некоторого времени им можно пренебречь и остаётся только частные решения неоднородного уравнения (без вывода) 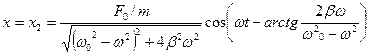(14)

Функция (14) описывает установившиеся вынужденные гармонические колебания с частотой, равной частоте вынужденной силы.

Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных 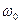и 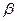) амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания также зависит от частоты вынуждающей силы.

Механический резонанс. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной частотой.

Чтобы найти резонансную частоту 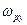, нужно найти максимум амплитуды функции (14), т.е. максимум функции 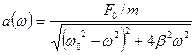(15)

Или, что-то же самое, найти минимум выражения, стоящего под корнем в знаменателе (15). Продифференцировав выражение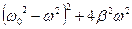

по 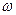и приравняв к нулю, получим

.

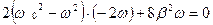Проведя дальнейшие простые преобразования, получим

,

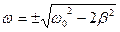а т.к. частота по своему смыслу не может быть отрицательной, то выбираем решение со знаком «+». Итак, резонансная частота

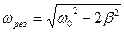(16)

Резонансная кривая - зависимость амплитуды установившихся колебаний маятника от частоты вынуждающей силы.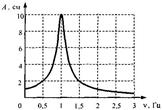

18)

Механические волны — это процесс распространения в пространстве колебаний частиц упругой среды (твёрдой, жидкой или газообразной).

Наличие у среды упругих свойств является необходимым условием распространения волн: деформация, возникающая в каком-либо месте, благодаря взаимодействию соседних частиц последовательно передаётся от одной точки среды к другой. Различным типам деформаций будут соответствовать разные типы волн.

Скоростью распространения волны называется отношение длины волны к периоду колебаний частиц среды:

v =λ/T

Частотой волны называется частота колебаний частиц:

ν =1/T

Отсюда получаем связь скорости волны, длины волны и частоты:

v = λν

Продольные и поперечные волны

Волна называется продольной, если частицы среды колеблются параллельно направлению распространения волны. Продольная волна состоит из чередующихся деформаций растяжения и сжатия.

Волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. Поперечная волна вызывается деформациями сдвига одного слоя среды относительно другого.

Продольные волны могут распространяться в твёрдых телах, жидкостях и газах: во всех этих средах возникает упругая реакция на сжатие, в результате которой появятся бегущие друг за другом сжатия и разрежения среды.

Однако жидкости и газы, в отличие от твёрдых тел, не обладают упругостью по отношению к сдвигу слоёв. Поэтому поперечные волны могут распространяться в твёрдых телах, но не внутри жидкостей и газов.

Уравнение плоской гармонической воны, распространяющейся вдоль оси x:

S=Acos((ωt-x/v)+φ0)

Закон Гука:

Сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.

F=-kx

u= (Eε^2)/2 - плотность энергии упругой деформации при растяжении (или сжатии)

W=m/2((〖∂ε/∂t)〗^2+v^2 (〖∂ε/∂x)〗^2)-энергия упругой волны

Плотность потока энергии - вектор, физическая величина j, численно равная потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно направлению переноса энергии.

Направление j (вектор!) совпадает с направлением переноса энергии

j=∆E/∆t∆S=∆ϕ/∆S

19)

Специальная теория относительности (СТО) представляет собой современную физическую теорию пространства и времени. СТО часто называют релятивистской теорией, а специфические явления, описываемые этой теорией, – релятивистскими эффектами. Эти эффекты наиболее отчетливо проявляются при скоростях движения тел, близких к скорости света в вакууме c ≈ 3·10⁸ м/с. Специальная теория относительности была создана А. Эйнштейном (1905 г.).

Классическая механика Ньютона прекрасно описывает движение макротел, движущихся с малыми скоростями (υ << c). В основе классической механики лежит механический принцип относительности: законы динамики одинаковы во всех инерциальных системах отсчета. Этот принцип означает, что законы динамики инвариантны (т. е. неизменны) относительно преобразований Галилея, которые позволяют вычислить координаты движущегося тела в одной инерциальной системе (K), если заданы координаты этого тела в другой инерциальной системе (K').

В основе специальной теории относительности лежат два принципа или постулата, сформулированные Эйнштейном в 1905 г.

1)Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна.

2)Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую.

Эти принципы следует рассматривать как обобщение всей совокупности опытных фактов.

Преобразования Лоренца

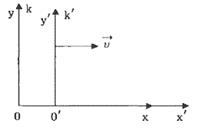
Пусть нам даны две системы отсчета k и k`. В момент t = 0 обе эти системы координат совпадают. Пусть система k` (назовем ее подвижной) движется так, что ось х` скользит по оси х, ось у` параллельна оси у, скорость v - скорость движения этой системы координат (рис. 109).

Точка М имеет координаты в системе k - х, у, z, a в системе k` - х`, у`, z`.

Преобразования Галилея в классической механике имеют вид:

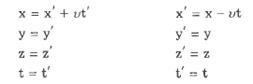
Преобразования координат, удовлетворяющие постулатам специальной теории относительности, называются преобразованиями Лоренца.

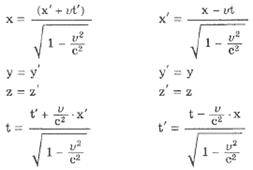
Следствия из преобразований Лоренца

1)Длина движущегося стержня.

Предположим, что стержень расположен вдоль оси х` в системе k` и движется вместе с системой k` со скоростью v.

Разность между координатами конца и начала отрезка в системе отсчета, в которой он неподвижен, называется собственной длиной отрезка. В нашем случае l₀ = х₂` - х<sub>1</sub>`, где х₂` - координата конца отрезка в системе k` и х/ - координата начала. Относительно системы k стержень движется. Длиной движущегося стержня принимают разность между координатами конца и начала стержня в один и тот же момент времени по часам системы k.

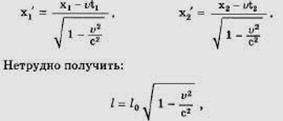
где l - длина движущегося стержня, l₀ - собственная длина стержня. Длина движущегося стержня меньше собственной длины.

2)Темп хода движущихся часов.

Пусть в точке х₀` движущейся системы координат k` происходит последовательно два события в моменты t₁ и t₂. В неподвижной системе координат k эти события происходят в разных точках в моменты t₁ и t₂. Интервал времени между этими событиями в движущейся системе координат равен дельта t` = t<sub>2</sub>` - t₁`, а в покоящейся дельта t = t₂ - t₁.

На основании преобразования Лоренца получим:

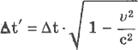
Интервал времени дельта t` между событиями, измеренный движущимися часами, меньше, чем интервал времени дельта t между теми же событиями, измеренный покоящимися часами. Это означает, что темп хода движущихся часов замедлен относительно неподвижных.

Время, которое измеряется по часам, связанным с движущейся точкой, называется собственным временем этой точки.

3)Относительность одновременности.

Из преобразований Лоренца следует, что если в системе k в точке с координатами x₁ и х₂ происходили два события одновременно (t₁ = t₂ = t₀), то в системе k` интервал

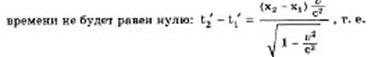
понятие одновременности - понятие относительное. События, одновременные в одной системе координат, оказались неодновременными в другой.

4)Относительность одновременности и причинность.

Из относительности одновременности следует, что последовательность одних и тех же событий в различных системах координат различна.

Не может ли случиться так, что в одной системе координат причина предшествует следствию, а в другой, наоборот, следствие предшествует причине?

Чтобы причинно-следственная связь между событиями имела объективный характер и не зависела от системы координат, в которой она рассматривается, необходимо, чтобы никакие материальные воздействия, осуществляющие физическую связь событий, происходящих в различных точках, не могли передаваться со скоростью, большей скорости света.

Таким образом, передача физического влияния из одной точки в другую не может происходить со скоростью, большей скорости света. При этом условии причинная связь событий носит абсолютный характер: не существует системы координат, в которой причина и следствие меняются местами.

Сложение скоростей

Непосредственным следствием преобразований Лоренца является релятивистское правило сложения скоростей. Если некоторый объект имеет компоненты скорости 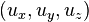относительно системы S и 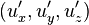— относительно S', то между ними существует следующая связь:

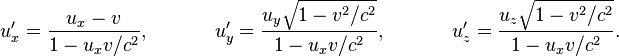
В этих соотношениях относительная скорость движения систем отсчёта v направлена вдоль оси x. Релятивистское сложение скоростей, как и преобразования Лоренца, при малых скоростях ( 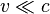) переходит в классический закон сложения скоростей.

Если объект движется со скоростью света 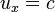вдоль оси x относительно системы S, то такая же скорость у него будет и относительно S': 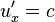. Это означает, что скорость является инвариантной (одинаковой) во всех ИСО.

Энергия и импульс

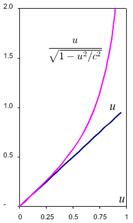Релятивистский и классический импульс, m=1

Если частица с массой (покоя) 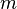движется со скоростью 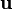, то её энергия и импульс имеют следующую зависимость от скорости:

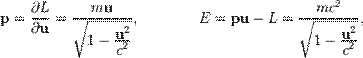
Эти соотношения обобщают классические выражения для энергии и импульса, получающиеся в результате разложения в ряд по :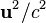

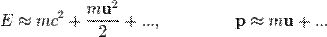
При нулевой скорости энергия частицы называется энергией покоя: 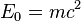. В современной физической литературе принято, что m — масса частицы не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной (то есть масса тела, состоящего из нескольких частей, в отличие от классической механики, не равна сумме масс этих частей). Понятие «релятивистской массы», зависящей от скорости 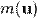не используется, хотя оно и встречается в ранних работах по теории относительности. Историческая причина введения этого понятия была связана с попытками сохранить для релятивистского импульса классическую форму: .

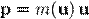При приближении скорости тела к скорости света его энергия и импульс стремятся к бесконечности. Это одна из причин, по которой «обычные» объекты не способны двигаться быстрее скорости света. Для частицы с ненулевой массой даже достижение скорости света потребует затраты бесконечной энергии. Заметные отклонения от классических выражений для энергии и импульса происходят при скоростях, близких к скорости света. Если скорости относительно невелики, то отклонения от классической динамики незначительны. Например, при скорости u=c/4 относительная разница релятивистского и классического импульса составляет всего 3 %.

Между релятивистской энергией и импульсом существуют следующие связи:

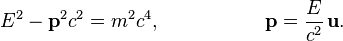
Эти формулы остаются справедливыми и для объектов, движущихся со скоростью света. В этом случае их масса покоя должна быть равна нулю .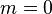

Преобразования энергии и импульса

Аналогично преобразованиям Лоренца для времени и координат релятивистские энергия и импульс, измеренные относительно различных инерциальных систем отсчёта, связаны аналогичными соотношениями:

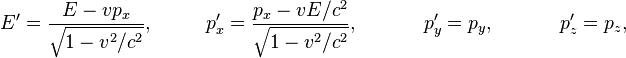
где компоненты вектора импульса 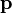равны 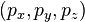. Относительная скорость и ориентация инерциальных систем отсчёта S, S' определены так же, как и в преобразованиях Лоренца.

20)

Идеальный газ — математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что: 1)потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объём частиц газа пренебрежимо мал; 3) между частицами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; 4) время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями. В рамках термодинамики идеальным называется газ, подчиняющийся термическому уравнению состояния Клапейрона — Менделеева.

Наши рекомендации