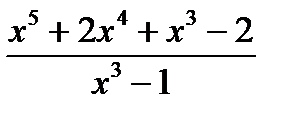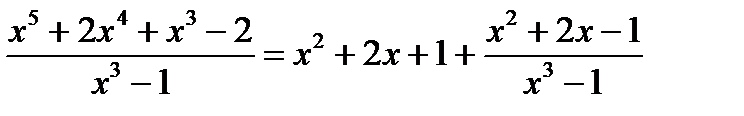Практическая часть нахождения касательной прямой и нормальной плоскости кривой
Применим все вышесказанное к нашей кривой: найдем касательную прямую и нормальную плоскость в произвольной и выбранной точке.
В уравнение касательной прямой:
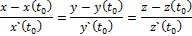
подставим наши координаты: x,yи z вместо 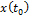 ,
, 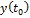 и
и 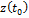 соответственно, и производные
соответственно, и производные 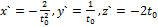 вместо
вместо 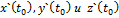 , получим:
, получим:
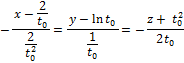
Мы получили уравнение касательной прямой в общем виде, теперь найдем уравнениепрямой в выбранной точке, приняв 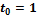 :
:
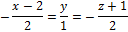
Нами получено уравнение касательной прямой в выбранной точке.Теперь найдем уравнение нормальной плоскости кривой, по аналогии с нахождением уравнения касательной прямой, подставив в формулу:
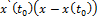 +
+ 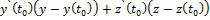 =0
=0
наши координаты:
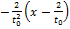 +
+ 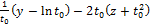 =0.
=0.
Уравнение нормальной плоскости кривой в произвольной точке найдено. Напишем уравнение в выбранной точке, напомню, что 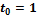 . В итоге получаем:
. В итоге получаем:
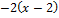 +
+ 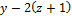 =0.
=0.
Нами получено уравнение нормальной плоскости кривой в выбранной точке.
8. Условный экстремум. Определение. Необходимые условия. Метод множителя Лагранжа. Формулировка достаточных условий.
Условный экстремум - относительный экстремум, экстремум функции f (x1,..., xn + m) от п+т переменных в предположении, что эти переменные подчинены ещё т уравнениям связи (условиям): φk (x1,..., xn + m) = 0, 1≤ k ≤ m (*) Точнее, функция f имеет условный экстремум (У.э.) в точке М, координаты которой удовлетворяют уравнениям (*), если её значение в точке М является наибольшим или наименьшим по сравнению со значениями f в точках некоторой окрестности точки М, координаты которых удовлетворяют уравнениям (*).
Определение 5.4.Если аргументы функции f (x1 , x2 ,…, xn) связаны дополнительными условиями в виде m уравнений (m < n):
φ1 (х1, х2 ,…, хn) = 0, φ2 (х1, х2 ,…, хn) = 0, …, φm (х1, х2 ,…, хn) = 0, (5.2)
где функции φi имеют непрерывные частные производные, то уравнения (5.2) называются уравнениями связи.
Определение 5.5.Экстремум функции f (x1 , x2 ,…, xn) при выполнении условий (5.2) называется условным экстремумом.
Замечание. Можно предложить следующее геометрическое истолкование условного экстремума функции двух переменных: пусть аргументы функции f(x,y) связаны уравнением φ(х,у) = 0, задающим некоторую кривую в плоскости Оху. Восставив из каждой точки этой кривой перпендикуляры к плоскости Оху до пересечения с поверхностью z = f (x,y), получим пространственную кривую, лежащую на поверхности над кривой φ(х,у) = 0. Задача состоит в поиске точек экстремума полученной кривой, которые, разумеется, в общем случае не совпадают с точками безусловного экстремума функции f(x,y).
Определение 5.6.Функция L (x1 , x2 ,…, xn) = f (x1 , x2 ,…, xn) + λ1φ1 (x1 , x2 ,…, xn) +
+ λ2φ2 (x1 , x2 ,…, xn) +…+λmφm (x1 , x2 ,…, xn), (5.3)
где λi – некоторые постоянные, называется функцией Лагранжа, а числа λi – неопределенными множителями Лагранжа.
Теорема 5.3 (необходимые условия условного экстремума). Условный экстремум функции z = f (x, y) при наличии уравнения связи φ (х, у) = 0 может достигаться только в стационарных точках функции Лагранжа L (x, y) = f (x, y) + λφ (x, y).
Доказательство. Уравнение связи задает неявную зависимость у от х, поэтому будем считать, что у есть функция от х: у = у(х). Тогда z есть сложная функция от х, и ее критические точки определяются условием: 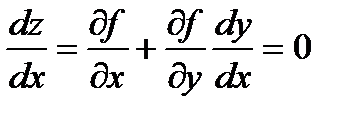 . (5.4) Из уравнения связи следует, что
. (5.4) Из уравнения связи следует, что 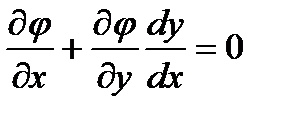 . (5.5)
. (5.5)
Умножим равенство (5.5) на некоторое число λ и сложим с (5.4). Получим:
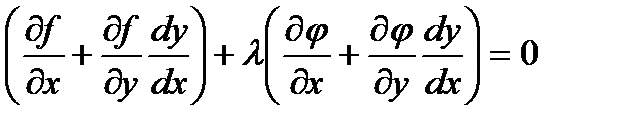 , или
, или 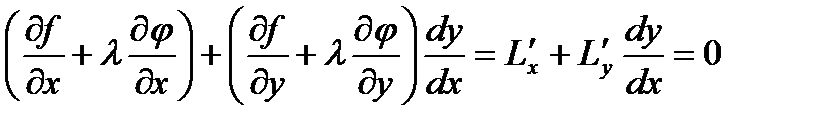 .
.
Последнее равенство должно выполняться в стационарных точках, откуда следует:
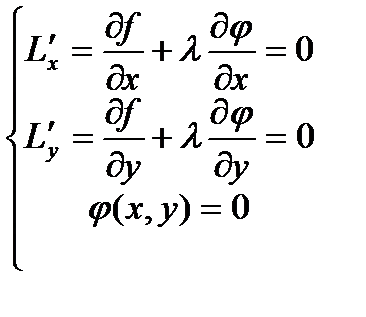 (5.6)
(5.6)
Получена система трех уравнений относительно трех неизвестных: х, у и λ, причем первые два уравнения являются условиями стационарной точки функции Лагранжа. Исключая из системы (5.6) вспомогательное неизвестное λ, находим координаты точек, в которых исходная функция может иметь условный экстремум.
9. Первообразная. Неопределенный интеграл, его свойства. Интегрирование по частям и замена переменной в неопределенном интеграле.
Определение 6.1. Функция F(x) называется первообразной (для) функции f(x) на некотором множестве значений х, если F΄(x) = f(x) на этом множестве.
Теорема 6.1.Если функции F(x) и G(x) являются первообразными одной и той же функции f(x) на некотором множестве, то необходимым и достаточным условием этого является то, что G(x) = F(x) + C, где С – любая постоянная.
Доказательство.
- Пусть F(x) - первообразная f(x), то есть F΄(x) = f(x). Тогда для любого числа C (F(x) + C)΄= F΄(x) + C΄= F΄(x) + 0 = f(x), то есть F(x) + C - первообразная f(x).
- Пусть F(x) и G(x) – две различные первообразные одной и той же функции f(x). Тогда (F(x) – G(x))΄= F΄(x) - G΄(x) = f(x) – f(x) = 0, следовательно, F(x) – G(x) = C (по следствию из теоремы Лагранжа). Теорема доказана.
Таким образом, если функция на данном множестве имеет одну первообразную, то она имеет их бесконечно много, причем все они отличаются друг от друга постоянными слагаемыми.
Определение 5.2. Совокупность всех первообразных функции f(x) на некотором множестве называется ее неопределенным интегралом.
Обозначение: 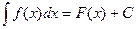 .
.
f(x) при этом называется подынтегральной функцией, а f(x)dx – подынтегральным выражением.
Свойства неопределенного интеграла.
1. 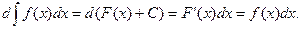
2. 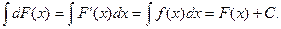
3. 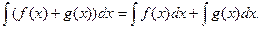 Действительно,
Действительно, 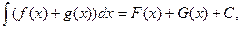 а
а 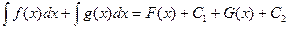 . Но, поскольку С1+С2 – произвольная постоянная, выражения в левой и правой частях равны.
. Но, поскольку С1+С2 – произвольная постоянная, выражения в левой и правой частях равны.
4. 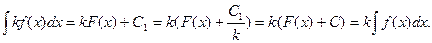
Замечание. Все перечисленные свойства формулировались и доказывались в предположении, что на некотором множестве существуют первообразные функций f(x) и g(x), равные соответственно F(x) и G(x).
Табличные интегралы.
Из определения первообразной и неопределенного интеграла следует, что таблицу основных интегралов можно получить из таблицы основных производных (см. лекцию 18 первой части курса), считая производные табличных функций подынтегральными функциями, а сами функции – их первообразными.
1. 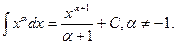 2.
2. 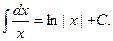
3. 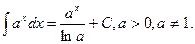 3΄)
3΄) 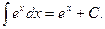
4. 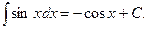 5.
5. 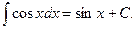
6. 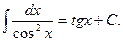 7.
7. 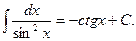
8. 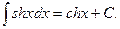 9.
9. 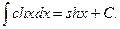
10. 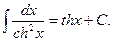 11.
11. 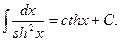
12. 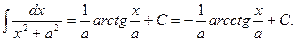
13. 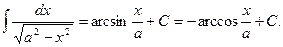
Можно добавить к этой таблице еще несколько формул, не следующих непосредственно из таблицы производных, но удобных для вычисления многих интегралов, а именно:
14. 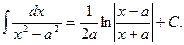 15.
15. 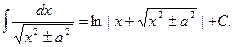
Доказательство справедливости этих формул предлагается провести самостоятельно.
Примеры.
1. 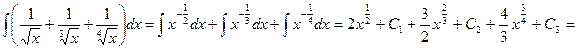
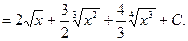
2. 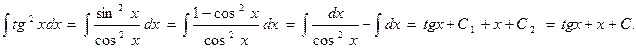
Теорема 6.2. Пусть функция f(x) определена на множестве Х, а функция φ(t) – на множестве Φ, причем 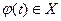
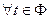 . Тогда, если функция f(x) имеет первообразную F(x) на Х, а φ(t) дифференцируема на Φ, то
. Тогда, если функция f(x) имеет первообразную F(x) на Х, а φ(t) дифференцируема на Φ, то
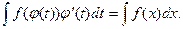 (6.1)
(6.1)
Доказательство.
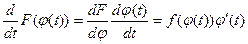 , поэтому функция F(φ(t)) является первообразной функции f(φ(t)) φ΄(t). Следовательно,
, поэтому функция F(φ(t)) является первообразной функции f(φ(t)) φ΄(t). Следовательно, 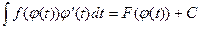 . С другой стороны, при x = φ(t)
. С другой стороны, при x = φ(t) 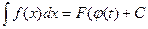 . В полученных формулах равны правые части, следовательно, равны и левые, что доказывает справедливость формулы (6.1).
. В полученных формулах равны правые части, следовательно, равны и левые, что доказывает справедливость формулы (6.1).
Замечание 1. Формулу (6.1) называют формулой интегрирования подстановкой.
Замечание 2. Часто удобно бывает использовать формулу (6.1) «в обратную сторону»:
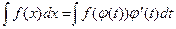 , (6.2)
, (6.2)
то есть заменять переменную х функцией новой переменной t. Формула (6.2) носит название формулы интегрирования заменой переменной.
Замечание. Формулы (6.1) и (6.2) показывают, что вид первообразной не изменяется при замене независимой переменной х на функцию φ(t), поэтому их называют формулами инвариантности интегрирования.
Примеры.
1. 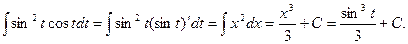 При этом была сделана подстановка x = sin t.
При этом была сделана подстановка x = sin t.
2. 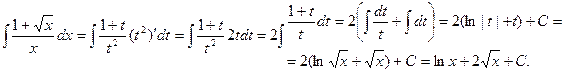
Интеграл был вычислен с помощью замены переменной: x = t².
Теорема 6.3. Если функции u(x) и v(x) дифференцируемы на некотором промежутке, и на нем существует интеграл 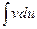 , то на нем существует и интеграл
, то на нем существует и интеграл 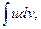 причем
причем
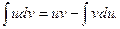 (6.3)
(6.3)
Доказательство.
d(uv) = vdu + udv, поэтому udv = d(uv) – vdu. Проинтегрируем обе части полученного равенства, учитывая, что 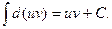 Тогда
Тогда 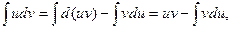 что и требовалось доказать. Существование интеграла в левой части равенства следует из существования обоих интегралов в правой части
что и требовалось доказать. Существование интеграла в левой части равенства следует из существования обоих интегралов в правой части
10. Основные сведения из алгебры многочленов. Разложение многочлена с действительными коэффициентами. Разложение правильной рациональной дроби на элементарные дроби.
Предварительные сведения из алгебры многочленов
а) Если a вещественный корень многочлена , то существует единственное представление многочлена в виде
P(x) = (x – a)a P1(x), a³1, P1(a)¹0.
Число a называется кратностью корня. Другое эквивалентное определение кратности корня дается в терминах производных: a – это порядок первой, не равной нулю производной в точке a: P(a)= P¢(a)=…= P(a-1)(a)=0, P(a)(a)¹0.
б) Если w = u + i v, v¹0 комплексный корень многочлена с действительными коэффициентами, то сопряженное комплексное число 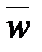 = u - i v также является корнем многочлена. Это утверждение следует из свойств операции комплексного сопряжения:
= u - i v также является корнем многочлена. Это утверждение следует из свойств операции комплексного сопряжения: 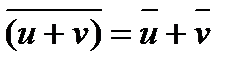 ,
, 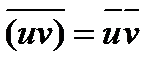 , для действительного числа x справедливо равенство
, для действительного числа x справедливо равенство 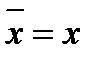 . Поэтому, если w корень многочлена P(x) = a0+…+akxk+…+ anxn , то
. Поэтому, если w корень многочлена P(x) = a0+…+akxk+…+ anxn , то 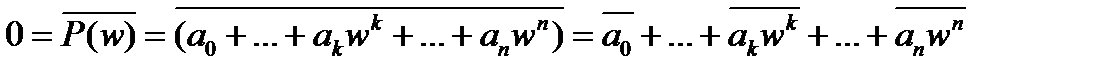 =
= 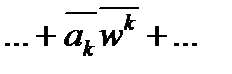 =
= 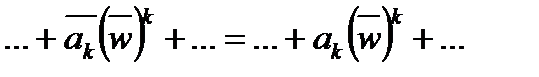 =P(
=P( 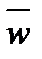 ).
).
Тогда существует единственное представление многочлена в виде
P(x) = (x2+px+q)b P1(x), b³1, P1(w)¹0,
(x - w)(x - 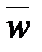 )=(x - u - i v)(x - u + i v)=(x-u)2+v2=x2-2ux+u2+v2= x2+px+q.
)=(x - u - i v)(x - u + i v)=(x-u)2+v2=x2-2ux+u2+v2= x2+px+q.
в) Любой многочлен можно разложить в произведение по своим корням
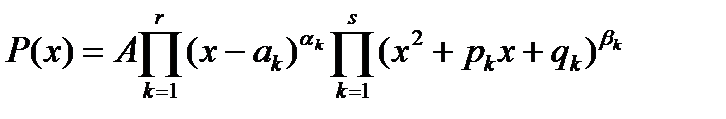 ,
,
где A – старший коэффициент многочлена, a1,a2,…, ar -действительные корни кратностей a1,a2,…, ar , а w1,w2,…, ws комплексные корни кратностей b1,b2,…, bs. Связь между комплексными корнями и сомножителями в разложении многочлена следующая x2+pkx+qk=(x - wk)(x - 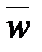 k).
k).
Определение. Рациональная функция ( отношение двух многочленов) 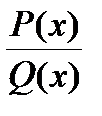 ) называется правильной дробью, если порядок многочлена числителя строго меньше порядка многочлена в знаменателе.
) называется правильной дробью, если порядок многочлена числителя строго меньше порядка многочлена в знаменателе.
Утверждение. Любую рациональную функцию можно представить в виде многочлена (целая часть) плюс правильная дробь .
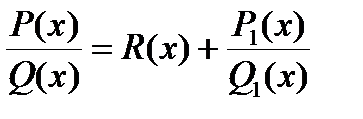 , - R(x) – многочлен, дробь
, - R(x) – многочлен, дробь 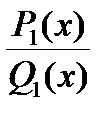 - правильная.
- правильная.
R(x) –называется целой частью, а дробь P1/Q1 –остатком. Остаток и целую часть можно получить делением «уголком».
Пример: