Санкт-петербургский государственный

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

_______________________________________________________

Н.А. МАСЛЕННИКОВ, В,М, ПЕТРОВ

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА.

СБОРНИК ЗАДАНИЙ

ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ

Для студентов ФБФО, изучающих предмет в один семестр

Методические указания

Санкт-Петербург

УДК 624.014:625.08.001.24

Рецензент:

В.П. Колосов - к-т техн. наук, доцент СПбГАСУ

Н.А. Масленников, В.М. Петров Теоретическая механика. Сборник заданий для расчетно-графических работ. Методические указания – СПб: СПбГАСУ, 2016. - 27 с.

Библ.: 5 назв. Таб. 4, рис. 4.

Предназначены для студентов дневной и вечерней формы обучения

«Теоретическая механика»

Методические указания рекомендованы на заседании кафедры «Механики» от 16.10.2016 г., протокол № 2

Методические указания публикуется в

Авторской редакции

© Н.А. Масленников, В.М. Петров 2016

Содержание расчётно-графических работ

РГР № 1. Равновесие плоской системы связанных тел..

РГР № 2. Теорема об изменении кинетической энергии.

РГР № 3. Принцип возможных перемещений для определения реакций опор в шарнирной балке

Порядок получения индивидуального задания

Исходные данные для выполнения каждой работы студент выписывает из приведённых в каждом задании таблиц и схем в соответствии со своим шифром. Шифром являются три последних цифры номера зачётной книжки или студенческого билета. Например, номер зачётной книжки 18549: первая цифра шифра –5, вторая –4, третья –9.

Общие требования к оформлению расчётно-графических работ

Расчётно-графическая работа выполняется на стандартных листах писчей бумаги (формат А–4). Заполняется только одна сторона листа.

(см. приложение 1, стр.32). На титульном листе указываются номер и название работы, фамилия, имя и отчество студента, номера группы и специальности, индивидуальный шифр. Работа должна быть сброшюрована. Расчётная схема изображается в масштабе длин. На ней указываются все необходимые данные в численном виде (размеры, нагрузки и др.), которые выписываются из таблиц. Все расчёты приводятся в краткой форме.

Небрежно выполненные и выполненные не по шифру работы к проверке не принимаются.

Рекомендуемая литература

1. Павлов В.Е. Теоретическая механика: учеб. Пособие для студ. Высш. Учеб. Заведений /В.Е. Павлов, Ф.А. Доронин. – М.: Издательский центр «Академия», 2009. – 320 с.

2. Бутенин Н.В., Яков Л., Меркин Д.Р. Курс теоретической механики. В 2-х томах. 10 изд. – М.:Лань, 2009.

3. Сборник задач для курсовых работ по теоретической механике под ред. А.А. Яблонского. – М.: ЕЕ Медия, 2012. – 388 с.

4. Мещерский И. Задачи по теоретической механике. - М.:Лань, 2009.

5. Масленников Н.А. и др. Сборник заданий и руководство по выполнению курсовой работы по статике. Учебное пособие. – СПб: Петербургский гос. Ун-т путей сообщения, 2004. – 68 с.

РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 1

РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 2

Пример расчёта

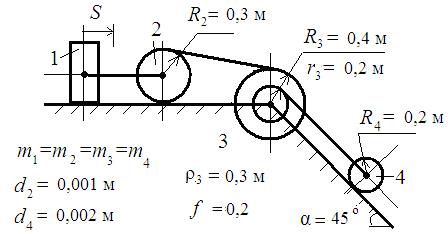
Определить скорость, которую приобретает тело 1, начинающее движение из состояния покоя и проделавшее путь S = 2м. Массы всех тел приять равными.

f – коэффициент трения скольжения,

d₂ и d₄ - коэффициенты трения качения,

m – масса тел,

ρ₃ – радиус инерции блока 3.

• Теорема об изменении кинетической энергии системы:

Т - Т_о = 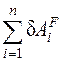+ 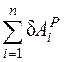; Т_о = 0; 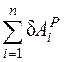= 0;

Следовательно, Т = .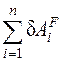

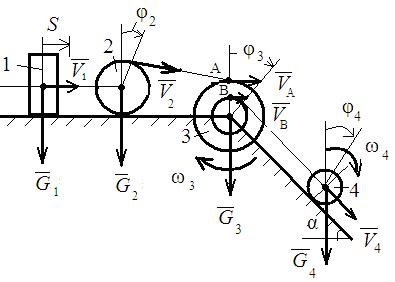
• Для определения кинетической энергии Т и суммы работ внешних сил изображаем систему в конечном положении.

• Устанавливаем кинематическое соотношение между скоростями и перемещениями точек системы, выражая скорости и перемещения тел через скорость и перемещение тела 1.

примем: R₃ = 0,4 м = R; тогда r₃ = 0,2 м = 0,5 ∙ R; R₄ = 0,2 м = R; R₂ = 0,3 м = 0,75∙ R;

• примем: V₁ = V; так как нити нерастяжимы, то V₂ = V₁ = V, V_А = V₂= V; V_В = 0,5 ∙ V_А = 0.5 V; V₄ = V_В = 0,5∙ V

V₂ = ω₂ ∙ R₂ ; V₂ = V; R₂= 0.75 ∙ R; ω₂ = 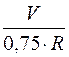= 1,333 ∙ ;

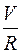V₃ = ω₃ ∙ R₃ ; V₃ = V; R₃ = R; ω₃ = ;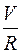

V₄ = ω₄ ∙ R₄; V₄ = 0,5 ∙ V; R₄ = 0,5 ∙ R; ω₄ = ;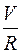

• примем S₁ = S; так как нити нерастяжимы, то S₂ = S₁ = S_A = S₃ = S;

S₂ = φ₂ ∙ R₂; R₂ = 0,75 ∙R; S₂ = S; φ₂ = 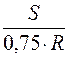= 1,333 ∙ ;

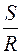S₃ = φ₃ ∙ R₃; R₃ = R; S₃ = S; φ₃ = ;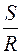

S_B = φ₃ ∙ r₃; r₃ = 0,5 ∙ R₃ = 0,5 ∙ R; S_B = 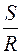∙ 0.5 ∙ R = 0,5 ∙ S ;

так как нити нерастяжимы, то S₄ = S_B = 0.5 ∙ S.

S₄ = φ₄ ∙ R₄; R₄ = 0,5 ∙ R; φ₄ = ;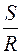

• Вычисляем кинетическую энергию системы в конечном положении, как сумму кинетических энергий всех тел: Т = ΣТ_i .

Т₁ = 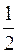∙ m₁ ∙ V₁² = 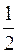∙ m ∙ V ² = 0,5 ∙ m ∙ V ² ;

Т₂ = 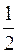∙ m₂ ∙ V₂² + 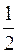∙ I₂ ∙ ω₂² = 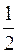∙ m ∙ V ² + 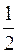∙ 0,28 ∙ m ∙ R² ∙ (1,33 ∙ 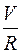)² = 0,75 ∙ m ∙ V ²;

I₂ = 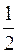∙ m₂ ∙ R₂² = 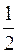∙ m ∙ (0,75 ∙ R)² = 0,28 ∙ m ∙ R²;

Т₃ = 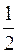∙ I₃ ∙ ω₃² = 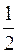∙ 0,5625 ∙ m ∙ R² ∙ ( 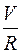)² = 0,28 ∙ m ∙ V ²;

I₃ = m₃ ∙ ρ₃² = m ∙ (0,75 ∙ R)² = 0.5625 ∙ m ∙ R² ;

(ρ₃ = 0,3 м = 0,75 ∙ R);

Т₄ = 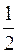∙ m₄ ∙ V₄² + 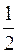∙ I₄ ∙ ω₄² = 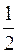∙ m ∙ (0,5 ∙ V)² + 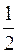∙ 0,125 ∙ m ∙ R² ∙ ( 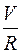)² = 0,1875 ∙ m ∙ V ²;

I₄ = 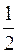∙ m₄ ∙ R₄² = 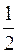∙ m ∙ (0,5 ∙ R)² = 0.125 ∙ m ∙ R²;

T = T₁ + T₂ + T₃ + T₄ = 0,5 ∙ m ∙V ² + 0,75 ∙ m ∙ V ² + 0,28 ∙ m ∙ V ² + 0,1875 ∙ m ∙ V ²

T = 1,72 ∙ m ∙ V ²

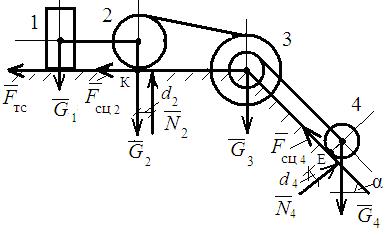
• Чертим схему системы с приложенными к ней внешними силами.

Так как по условию m₁ = m₂ = m₃ = m₄ = m , то G₁ = G₂ = G₃ = G₄ = G;

• Определяем сумму работ внешних сил, приложенных к системе, на заданном её перемещении.

Работа сил сцепления F_{cц 2} и F_{cц 4} равна нулю, так как эти силы приложены в неподвижных точках (мгновенных центрах скоростей тел 2 и 4).

ΣА = А_1тс + А_2тк + А_4тк + А_4G .

Работа силы трения скольжения тела 1: (R = 0,4 м, S = 2 м)

А_1тс = – F_1тс ∙ f ∙ S = – G ∙ f ∙ S = – 0.2 ∙ 2 ∙ G = – 0,4 ∙ G;

Работа пары сил сопротивления качению катка 2:

А_2тк = – М_2тк ∙ φ₂ = – N₂ ∙ d₂ ∙ φ₂ = – G ∙ 0,001 ∙ 1,333 ∙ =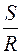

– 0,0013 ∙ G ∙ ∙ ;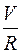

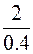А_2тк = – 0,0067 ∙ G;

Работа пары сил сопротивления качению катка 4:

А_4тк = – М_4тк ∙ φ₄ = – N₄ ∙ d₄ ∙ φ₄= – G ∙ cos45^o ∙ 0,002 ∙ =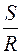

– G ∙ 0,707 ∙ 0,002 ∙ ;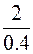

А_4тк = – 0.0071 ∙ G;

Работа силы тяжести катка 4:

А_4G = – G ∙ cos45^o ∙ S₄ = – G ∙ 0,707 ∙ 0.5∙ S = – 0,707 ∙ 0,5 ∙ 2 ∙ G =

– 0,707 ∙ G;

А = – 0,4 ∙ G – 0,0067 ∙ G – 0,0071 ∙ G – 0,707 ∙ G = 1,121 ∙ G =

1,121 ∙ m ∙ g = 11 ∙ m ;

• Используя теорему об изменении кинетической энергии, определяем скорость, которую приобретает тело 1: 1,72 ∙ m ∙ V ² = – 11 ∙ m;

V = 2,53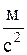

Пример расчёта

Для составной балки (рис.а), на которую действуют силы, указанные на схеме, определить реакции опор А, С и Е.

• Заменяем равномерно - распределённую нагрузку сосредоточенной силой Q = q ∙ a = 1 ∙ 2 = 2 кН.

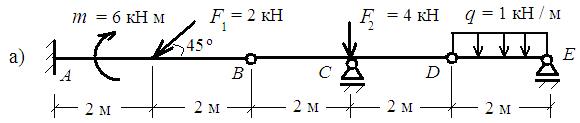
• Определяем реакцию опоры Е. (рис. б).

Отбрасываем опору Е, заменяя её реакцией R_E. Балка DE повернётся вокруг цилиндрического шарнира D на бесконечно малый угол δφ₁. Все остальные точки не имеют возможных перемещений.

Чертим схему возможных перемещений.

Из подобия треугольников: δs_q = 0,5 ∙ δs_E;

Составляем уравнение работ и решаем его, определяя искомую реакцию: 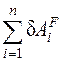= R_E ∙ δs_E – Q ∙ δs_q = 0; R_E ∙ δs_E = 2 ∙ 0,5δs_Е; R_E = 1кН

• Аналогично определяем реакцию опоры С. (рис. в).

Опору С заменяем реакцией R_С. Балка DE повернётся на бесконечно малый угол δφ₃ вокруг цилиндрического шарнира Е, а балка BD - вокруг шарнира В на угол δφ₂. Все остальные точки не имеют возможных перемещений. Чертим схему возможных перемещений.

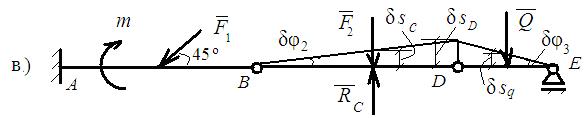
Из подобия треугольников: δs_q = δs_С = 0,5 ∙ δs_D ;

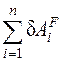= 0; R_С ∙ δs_С – F₂ ∙ δs_С - Q ∙ δs_q = 0;

R_С ∙ 0,5 ∙ δs_D – 4 ∙ 0,5 ∙ δs_D – 2 ∙ 0,5 ∙ δs_D = 0; R_C = 6 кН;

• Определяем горизонтальную составляющую реакции опоры А

(рис. г). Для этого заменяем жёсткое защемление опорой в виде ползуна, жёстко скреплённого с балкой. Такая опора позволяет исключить горизонтальную связь опоры А, которая компенсируется реакцией Х_А, но не допускает вертикальное перемещение и поворот. В этом случае система получает одну степень свободы.

А возможные перемещения будут только горизонтальными, одинаковыми для всех тел – δs.

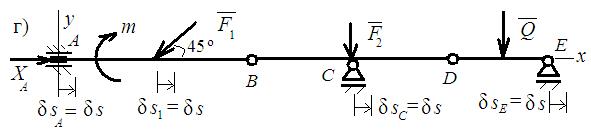
Уравнение работ получает вид: 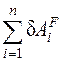= 0 ;

Х_А ∙ δs – F₁ ∙ cos45^o ∙ δs = 0; X_A – 2 ∙ 0,707 = 0; Х_А = 1,414 кН;

• Определяем вертикальную составляющую реакции опоры А (рис. д).

Для этого ползун располагаем вертикально, и вертикальная связь компенсируется вертикальной реакцией Y_А (по аналогии с предыдущей горизонтальной связью).

При сообщении системе возможных перемещений балка АВ получит поступательное вертикальное перемещение, балка ВD повернётся вокруг цилиндрического шарнира С, а балка DЕ - вокруг шарнира Е.

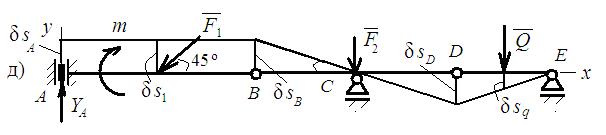
Из подобия треугольников: δs_А = δs₁ = δs_B =δs_D ; δs_q = 0,5 ∙ δs_D ;

Уравнение работ получает вид: 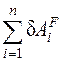= 0;

Y_А ∙ δs_А – F₁ ∙ sin 45^o ∙ δs₁ + Q ∙ δs_q = 0; Y_A – 2 ∙ 0,707 + 2 ∙ 0,5 = 0;

Y_А = 0,414 кН;

• Определяем реактивный момент опоры А. Для этого заменяем жёсткое защемление шарнирно-неподвижной опорой, а отброшенную связь – реактивным моментом М_А. (рис. е).

Даём системе возможные перемещения и определяем зависимости между ними.

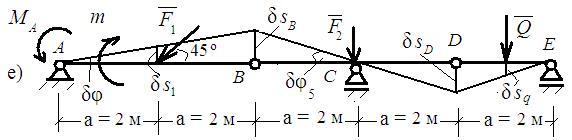
δs_B = δs_D = δs = 2а ∙ δφ = 4 ∙ δφ; δs_q = δs₁ =0,5 ∙ δs = 2 ∙ δφ;

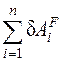= 0; М_А ∙δφ – m ∙ δφ – F₁ ∙ sin 45^o ∙ δs₁ + Q ∙ δs_q = 0;

М_А ∙ δφ – 6 ∙ δφ – 2 ∙ 0.707 ∙ 2 ∙ δφ + 2 ∙ 2 ∙ δφ = 0; М_А = 4,824кН∙м;

ПРИЛОЖЕНИЕ

Образец оформления первого листа расчета

(формат листа А-4)

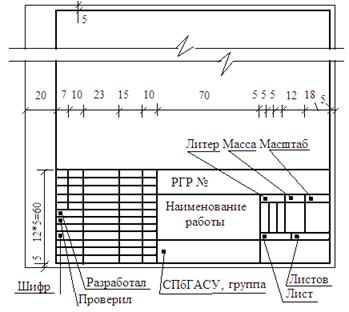
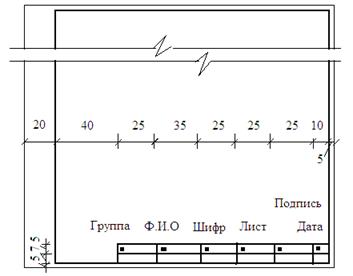
Образец оформления последующих листов расчета

(формат листа А-4)

Содержание

РГР № 1. Равновесие плоской системы связанных тел ……… 4

РГР № 2. Теорема об изменении кинетической энергии ……….. 7

РГР № 3. Принцип возможных перемещений для определения реакций опор в шарнирной балке ………………………………………15

ПРИЛОЖЕНИЕ…………………………………………………… 20

Масленников Никита Александрович

Теоретическая механика.

Сборник заданий

для расчетно-графических работ

Методические указания

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

_______________________________________________________

Н.А. МАСЛЕННИКОВ, В,М, ПЕТРОВ

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА.

СБОРНИК ЗАДАНИЙ