Свободные незатухающие электромагнитные колебания в колебательном контуре.

Свободные незатухающие электромагнитные колебания можно получить в электрической цепи, состоящей из последовательно соединенных конденсатора емкостью С, катушки индуктивностью L и резистора сопротивлением R:

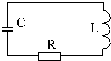Такую электрическую цепь называют колебательным контуром, потому что в ней могут происходить периодические изменения электрического заряда и разности потенциалов на обкладках конденсатора, а также электрического тока в цепи. Периодические колебания перечисленных физических величин достаточно вызвать даже при кратковременном подключении конденсатора колебательного контура к источнику постоянного тока. Однако, из-за потерь электрической энергии, связанной с нагреванием катушки и резистора, имеющих электрическое сопротивление R, колебания в контуре будут затухающими.

Свободные незатухающие электромагнитные колебания можно получить только в идеализированном случае, когда можно пренебречь электрическим сопротивлением (R 0) контура. Такие свободные незатухающие колебания называют еще собственными электромагнитными колебаниями.

Можно доказать, что в колебательном контуре происходят гармонические колебания заряда, согласно закону:

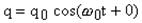, (1) или 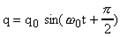, (2)

где : q - мгновенное значение заряда конденсатора;

q₀ - амплитудное значение электрического заряда;

w₀ - собственная частота колебаний в контуре.

Форма записи (через cos или sin) не имеет значения, так как отличие будет определяться лишь начальными условиями, а именно различной начальной фазой колебаний. Зная связь между зарядом конденсатора и разностью потенциалов на его обкладках:

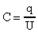, (3)

можно аналогично записать гармонические колебания разности потенциалов:

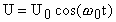, (4) или 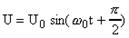, (5)

где: U - мгновенное значение напряжения на обкладках конденсатора;

U₀ - амплитудное значение напряжения;

w₀ - собственная частота колебаний в контуре.

Сила тока является первой производной от электрического заряда по времени:

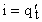. (6)

Поэтому гармонические колебания силы тока в колебательном контуре будут происходить по закону:

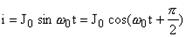, (7)

где: i - мгновенное значение тока в контуре;

J₀ = q₀ w₀ - амплитудное значение тока;

w₀ - собственная частота колебаний в контуре.

Циклическая частота w₀ называется собственной частотой электромагнитных колебаний, она зависит только от параметров колебательного контура, а именно - от емкости конденсатора С и индуктивности L:

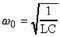. (8)

Период собственных электромагнитных колебаний, соответственно, вычисляется по формуле (Формула Томсона.):

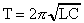. (9)

Физические процессы, происходящие в колебательном контуре, сопровождается непрерывными преобразованиями одного вида энергии в другой, а именно: энергия электрического заряда конденсатора превращается в энергию магнитного поля катушки и наоборот. При этом, в полном соответствии с законом сохранения и превращения энергии, полная энергия в колебательном контуре остается величиной постоянной:

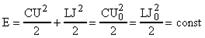, (10)

где: U и J - соответственно напряжение на обкладках конденсатора и сила тока в контуре в любой момент времени; U₀ и J₀ - амплитудные (максимальные) значения этих же величин.