Производные потенциала силы тяжести.

Производные потенциала силы тяжести по трем координатным осям , , однозначно определяют его полный вектор.

В частности, если ось z направить к центру Земли, то , а

В гравиметрии кроме первых производных изучаются вторые производные потенциала или их разности:

(1.3)

Физический смысл этих выражений легко получить, если иметь в виду, что . Так, например, вторая производная указывает на скорость изменения силы тяжести по оси х, т.е. является горизонтальным градиентом силы тяжести.

Аналогичный смысл имеют вторые производные и .

Вторые производные , характеризуют форму уровенной поверхности (геоида), изучаемую в геодезической гравиметрии. Практической единицей измерения градиента силы тяжести принимается 1 этвеш (Е)=10^-9/c², что соответствует изменению силы тяжести в 0,1 мГал на 1 км

Нормальное значение силы тяжести, редукции, аномалии силы тяжести и плотность горных пород

Нормальное значение силы тяжести.

Нормальным значением силы тяжести ( ) называется сила тяжести, обусловленная суточным вращением и притяжением Земли, в предположении, что она состоит из однородных по плотности концентрических слоев.

Принимая Землю за сфероид, Клеро получил следующую приближенную формулу для ее расчета:

где - сила тяжести на экваторе; - географическая широта пункта наблюдения; - коэффициент, зависящий от угловой скорости вращения и сжатия сфероида.

Однако Земля - геоид, и нормальные значения силы тяжести для его поверхности рассчитываются по формуле:

(1.4)

где - географическая долгота точки наблюдения.

Коэффициенты , и зависят от формы Земли, ее угловой скорости вращения, распределения масс. По многочисленным измерениям можно определить эти неизвестные коэффициенты. В настоящее время используется формула, в которой коэффициенты равны: , , и g_э=978,013 Гал.

Составлены специальные таблицы, по которым легко определить величину для любой точки земной поверхности. Измерив g_н в какой-то точке и вычтя , получим аномалию силы тяжести.

Таким образом, геоид является поверхностью относимости, по отношению к которой рассчитываются аномалии.

Редукции силы тяжести.

В наблюденные значения силы тяжести вводятся поправки (редукции). Введение поправок необходимо потому, что нормальные значения относятся к поверхности геоида, которая совпадает с уровнем океана, а измеренные значения относятся к действительной (реальной) земной поверхности. Для того, чтобы все наблюдения силы тяжести были сопоставимы, их приводят к одной поверхности - уровню геоида, т.е. как бы опускают точку наблюдения на этот уровень. Это осуществляется путем введения поправок за высоту, за притяжение промежуточного слоя и окружающий рельеф. Поправки называются редукциями.

Основными из них являются: поправка за высоту, за притяжение промежуточного слоя, за рельеф.

Для приведения измеренного значения к уровню океана вводят поправку за высоту ( ). Эту поправку называют поправкой за "свободный воздух" или поправкой Фая. Формула для расчета поправки за высоту имеет вид: , где в миллигалах, а (высота над уровнем моря) в метрах. Эта поправка должна прибавляться к измеренной силе тяжести, если точка наблюдений находится выше уровня геоида, и вычитаться, если ниже.

При введении поправки за притяжение промежуточного слоя ( ) вычисляется притяжение масс слоем между уровнем океана и данной точкой. Для расчета этой поправки используют формулу притяжения плоскопараллельной пластины, которая имеет вид: , где - абсолютная высота точки наблюдения в м, а - средняя плотность пород в этом слое в г/см³. Поправка имеет знак, противоположный знаку поправки за свободный воздух.

Для учета бокового притяжения рельефа местности, окружающего пункт наблюдения, при съемке в горных районах вводятся топографические поправки ( ). Имеется несколько способов учета таких поправок, которые всегда положительны.

При региональных исследованиях суши и океанов иногда используют специально рассчитываемые изостатические редукции, которые характеризуют отклонение от существующего в целом гидростатического равновесия Земли. Считается, что в верхней оболочке, называемой литосферой мощностью 100-200 км, такое равновесие достигается в основном посредством упругого изгиба. Глубже, в так называемой астеносфере с более низкой вязкостью, равновесие достигается горизонтальными течениями. От этих факторов зависит гидростатическое равновесие. В ряде районов с интенсивными изостатическими аномалиями оно нарушено.

Аномалии силы тяжести.

Аномалии силы тяжести рассчитываются по разным формулам. В геодезической гравиметрии под аномалией силы тяжести понимают разность между наблюденным значением ( $) и нормальным ( ) с учетом поправки Фая, она рассчитывается по формуле и называется аномалией Фая. Основной аномалией в гравиразведке является аномалия Буге:

(1.5)

в которую вводятся все поправки. Под понимается суммарная поправка в наблюденные значения, которая может быть определена до проведения работ, поскольку в ней имеются лишь топографические координаты точек наблюдения ( ). Ее рассчитывают с помощью ЭВМ.

Плотность горных пород.

Для постановки гравиразведки и особенно истолкования результатов необходимо знать плотность горных пород - , ибо это единственный физический параметр, на котором базируется гравиразведка.

Плотностью породы (или объемным весом) называется масса ( ) единицы объема породы ( 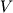) . Плотность измеряют в г/см³. Обычно плотность определяется для образцов, взятых из естественных обнажений, скважин и горных выработок. Наиболее простым способом определения плотности образца является взвешивание образца в воздухе ( ), и в воде ( ) и затем расчет . На этом принципе построен наиболее распространенный и простой прибор для измерения плотности - денситометр, позволяющий определять с точностью до 0,01 г/см³.

Для достоверности и представительности измерения следует производить на большом количестве образцов (до 50 штук). По многократным измерениям плотности образцов одного и того же литологического комплекса строятся вариационная кривая или график зависимости значений от количества образцов, обладающих данной плотностью. Максимум этой кривой характеризует наиболее вероятное значение плотности для данной породы. Существуют гравиметрические и другие геофизические способы полевых и скважинных определений плотности.

Плотность горных пород и руд зависит от химико-минералогического состава, т.е. объемной плотности твердых зерен, пористости и состава заполнителя пор (вода, растворы, нефть, газ). Плотность изверженных и метаморфических пород определяется в основном минералогическим составом и увеличивается при переходе от пород кислых к основным и ультраосновным. Для осадочных пород плотность определяется прежде всего пористостью, водонасыщенностью и в меньшей степени составом. Однако она сильно зависит от консолидации осадков, от их возраста и глубины залегания, с увеличением которых она растет. Примеры плотности даны в таблице 1.1.

Т а б л и ц а 1.1

Порода	Плотность (г/см3)
Нефть	0,8 -1,0
Уголь	1,0
Вода	1,1 - 2
Почва	1,13 - 2,0
Песок	1,4 - 2
Глина	2 - 2,2
Песчаник	1,8 - 2,8
Известняк	2,3 - 3,0
Соль	2,1 - 2,4
Гранит	2,4 - 2,9
Гнейсы	2,6 - 2,9
Габбро	2,8 - 3,1
Базальт	2,7 - 3,3
Перидотит	2,8 - 3,4
Медный колчедан	4,1 - 4,3
Магнетит, гематит	4,9 - 5,2
Плотность верхних частей земной коры (средняя)	2,67
Средняя плотность Земли	5,52
Плотность ядра Земли