Раздел 2. Основы теории графов

Раздел 2. Основы теории графов

Основные положения

Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий.

Определение графа можно дать как совокупности двух множеств V(точек) и E(линий, дуг), между элементами которых определено отношение инцидентности, причем каждый элемент е Î E инцидентен равно двум элементам v’,v” Î V. Элементы множества V называются вершинамиграфа G , элементы множества Е – его ребрами. Вершины и ребра графа G называют еще его элементами и вместо е Î Е и v ÎV пишут e Î G и v Î G.

В некоторых графах инцидентные ребру вершины неравноправны, они должны, например, рассматриваться в определенном порядке. Тогда каждому из ребер можно приписать направление от первой из инцидентных вершин ко второй. Направленные ребра часто называют дугами, а содержащий их граф – ориентированным. В противном случае

( инцидентные ребру вершины равноправны) граф будем называть неориентированным. Для ориентированного графа

Начало конец

1 2

Дуга: выходит входит

Наглядное представление о графе можно получить, если представить себе некоторое множество точек плоскости Х, называемых вершинами, и множество направленных отрезков U, соединяющих все или некоторые из вершин и называемых дугами. Математически граф G можно определить как пару множеств Х и U. G=(X,U) (1)

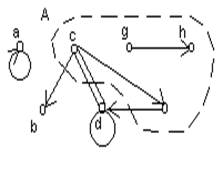На рисунке изображен граф, вершинами которого являются точки a, b, c, d, e, g, h, а дугами - отрезки (a,a), (c,b), (c,d), (c,e), (d,c), (d,d), (e,d), (g,h).

Рис.2.1 – Изображенние графа

Примерами графов являются отношения отцовства и материнства на множестве людей (родовое дерево), карта дорог на местности, схема соединений электрических приборов, отношении превосходства одних участников турнира над другими и т.п. Иногда бывает удобно дать графу другое определение. Можно считать, что множество направленных дуг U, соединяющих элементы множества Х, отображает это множество само в себя. Поэтому можно считать граф заданным, если дано множество его вершин Х и способ отображения Г множества Х в Х. Т.о., граф G есть пара (Х, Г), состоящая из множества Х и отображения Г, заданного на этом множестве G=(X,Г).

Так, для графа, изображенного на рис.2.1 отображение определяется следующим образом:

Г_a=a; Г_b=Æ; Г_c={b,d,e}; Г_d={c,d}; Г_e=d; Г_g=h; Г_h=Æ.

Нетрудно заметить, что данное определение графа полностью совпадает с определением отношения на множестве.

Введем некоторые понятия и определения, служащие для описания различных видов графов.

Подграфом G_A графа G=(X,Г) называется граф, в который входит лишь часть вершин графа G, образующих множество А, вместе с дугами, соединяющими эти вершины, например, очерченная пунктиром область А на рис.2.1. Математически подграф обозначается следующим образом:

G_A=(A,Г_A), где АÍХ, Г_АХ=(Г_Х)ÇА (2.1)

Частичным графом G_D по отношению к графу G=(X, Г) называется граф, содержащий только часть дуг графа G, т.е. определяемый условием:

G_D=(X, D), где Dx Í Г_X (2.2)

Например, пусть G=(X,Г) - карта шоссейных дорог Украины. Тогда карта шоссейных дорог Днепропетровской области представляет собой подграф, а карта главных дорог Украины - это частичный граф.

Другими важными понятиями для графа является понятие пути и контура. Дуга, соединяющая вершины a и b, и направленная от а к b обозначается u=(a,b).

Определения.

Путем в графе G называют такую последовательность дуг m=(u₁,...,u_k) , в которой конец каждой предыдущей дуги совпадает с началом следующей. Путь m, последовательными вершинами которого являются вершины a,b,...,m, обозначается через m=(a,b,...,m).

Длиной пути m=(u₁,...,u_k) называют число l(m)=k, равное числу дуг, составляющих путь. Иногда каждой дуге u_i приписывают некоторое число l(u_i), называемое длинной дуги. Тогда длинна пути определяется как сумма длин дуг, составляющих путь

_k

l (m)=S l(u_i) (2.3)

^I=1

Путь, в котором никакая дуга не встречается дважды, называется простым. Путь, в котором никакая вершина не встречается дважды, называется элементарным.

Контур - это конечный путь m=(x₁,...,x_k), у которого начальная вершина х₁ обязательно совпадает с конечной х_k. При этом контур называется элементарным, если все его вершины различны (за исключением начальной и конечной, которые совпадают). Контур единичной длинны, образованный дугой вида (а, а) называется петлей. Так, например, на рис. 1 (e, d, c, b) - путь, а (c, e, d, c) - контур, (d, d) - петля.

Иногда графы удобно представлять в виде некоторых матриц, в честности в виде матриц смежности и инцидентности. Предварительно дадим два определения.

Вершины x и y являются смежными, если они различны и если существует дуга, идущая из x в y.

Дугу u называют инцидентной вершине х, если она заходит в эту вершину или исходит из нее.

Обозначим через х₁,...,х_n вершины графа, а через u₁,...,u_m его дуги. Введем числа:

ì1, если имеется дуга, соединяющая вершину i с

r_ij = í вершиной j; (2.4)

î0, если такой дуги нет.

Квадратная матрица R=[r_ij] порядка (nxn) называется матрицей смежности графа.

Введем числа :

ì +1, если u_j исходит из x_i

S_ij= í -1, если u_j заходит в x_i (2.5)

î 0, если u_j не инцидентна x_i

Тогда матрица S=[S_ij] порядка (nxm) называется матрицей инцидентностидля дуг графа.

Матрицы инцидентности в описанном виде применимы только к графам без петель. В случае наличия в графе петель эту матрицу следует расчленить на две полу матрицы: положительную и отрицательную.

На рис.2.2 приведен граф без петель, для которого матрицы смежности и инцидентности имеют следующий вид:

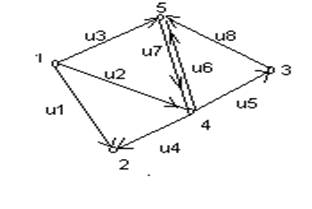
Матрица смежности.

i j
Ри.2.2. 4

Рис.2.2 – Граф без петель

Матрица инцидентности

i j
	-1			-1
					-1
		-1					-1
			-1			-1		-1

Обычно рассматриваемые графы конечны, т.е. конечны множества их элементов

( вершин и ребер). Поэтому конечностьэтих графов не будет специально оговариваться.

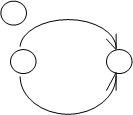
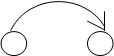
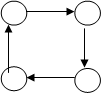
Примеры ориентированных графов:

а в с

d e f g к

(кратные ребра)

Рис.2.3 - Примеры ориентированных графов

В приведенных примерах вариант "в" представляет граф с пустым множеством ребер. Граф "е" иллюстрирует недостижимость двух вершин, а "g" – граф с петлей.

Неориентированные графы.

Иногда граф рассматривают без учета ориентации дуг, тогда его называют неориентированным графом. Понятие “дуга”, “путь” и “контур" для неориентированного графа заменяются понятиями “ребро”, “цепь”, “цикл”. Ребро - это отрезок, соединяющий 2 вершины. Цепь - последовательность ребер. Цикл - цепь, у которой начальная и конечная вершины совпадают. Описать неориентированный граф можно путем задания пары множеств (Х,U), где Х - множество вершин; U - множество ребер. Однако более удобным является описание неориентированного графа с помощью матрицы смежности или инцидентности, которые строятся аналогично соответствующим матрицам для ориентированных графов с той разницей, что не делается различия между заходящей в вершину и исходящей из нее дугами. При этом вершины х и y называют смежными, если существует соединяющее их ребро, а само это ребро называется инцидентным вершинам х и у.

Укажем еще несколько определений, служащих для характеристики неориентированных графов.

Степенью вершины х, обозначаемой deg(x) или dx, называют число ребер, инцидентных вершине х. Так для графа на рис.2.4 имеем d₁=2, d₂=2, d₃=3, d₄=1, d₅=0. Если d_x=1, то вершину называют тупиковой; если d_x=0 то вершину называют изолированной.

Теорема. Пусть G - неориентированный граф с n вершинами и m ребрами и d_j - степень j-й вершины тогда Sⁿ_j=1 d_j=2m.

Доказательство теоремы следует из того, что каждое ребро добавляет 1-цу к степени каждой из 2-х вершин, которые оно соединяет, т.е. добавляет 2 к сумме степеней уже имеющихся вершин.

Следствие. В каждом графе число вершин нечетной степени четно.

Для неориентированного графа понятия “подграф” и “частичный граф” аналогичны соответствующим понятиям для ориентированного графа.

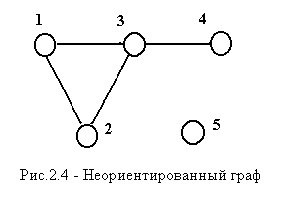С понятием неориентированного графа связана важная характеристика, называемая связностью графа. Говорят, что граф связен, если любые две его вершины можно соединить цепью. Если граф G не связен, то его можно разбить на такие подграфы G_i, что все вершины в каждом подграфе связны, а вершины из различных подграфов не связны. Такие подграфы G_i называют компонентами связности графа G. Если из графа (рис.2.4) исключить изолированную вершину 5, то полученный граф будет связным. Граф на рис.2.5 не связен и имеет две компоненты связности.

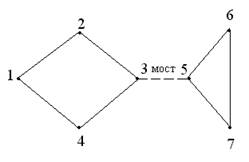Его можно превратить в связный, добавив ребро (мост), соединяющее вершины 3 и 5 (штриховая линия). Удаление моста превращает связной граф в несвязный.

Для того чтобы определить связность ориентированного графа не нужно обращать внимание на ориентацию дуг. Граф, изображенный на рис.1 является не связным.

Рис.2.5- Несвязный граф.

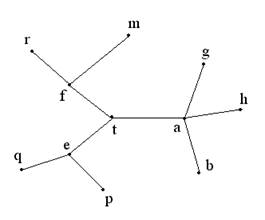Рис.2.6 - Граф в форме дерева

Однако его подграф, состоящий из вершин b,c,d,e является связным. Для ориентированного графа существует понятие сильной связности. Граф сильно связан, если для любых 2-х вершин (х и у, х¹у) существует путь, идущий из х в у. Важный частный случай неориентированного графа - дерево. (рис.2.6) Деревом называют конечный связный неориентированный граф, не имеющий циклов. Если дано множество вершин a,b,c,..., то дерево можно построить следующим образом. Одной из вершин например а, примем за начальную и назовем его корнем дерева. Из этой вершины проводим ребра в близлежащие вершины b, c, d,... из них проводим рёбра в соседние с ними вершины c, f, g, h,... и т.д. Т.о. дерево можно построить последовательно добавляя рёбра в его вершинах. Это даёт возможность установить связь между числом вершин и числом рёбер дерева. Простейшее дерево состоит из 2-х вершин, соединённых ребром. Каждый раз когда мы добавляем ещё одно ребро, в конце его прибавляется так же и вершина. Следовательно, дерево с n вершинами имеет n-1 рёбер.

Изоморфизм графов.

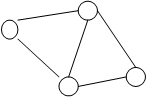
Один и тот же граф геометрически можно изобразить различными способами. Так на рис. 2.7 приведены три изображения одного и того же графа. Такие графы называются изоморфными.

1

1 2

2

1 4 3 4

4 3

2 3

Рис.2.7 - Пример изоморфных графов

Произвольный граф G имеет как минимум один автоморфизм - тождественное преобразование VG ® VG, при котором e(v) = v для произвольной вершины v. Очевидно, что если j - автоморфизм графа G, то й обратная подстановка j^-1 также является автоморфизмом. Если подстановки j і f обе суть автоморфизмы, те и их произведение jf - автоморфизм.

Характеристики графов.

Решение многих технических задач методами теории графов сводится к определению тех или иных характеристик графов, хотя технические приложения теории графов рассматривать в настоящей книге невозможно, знакомство с важнейшими характеристиками графов может оказаться полезным при изучении других дисциплин.

Цикломатическое число. Пусть G - неориентированный граф, имеющий n вершин, m рёбер и r компонент связности. Цикломатическим числом графа G называют число n(G)=m-n+r.

Это число имеет интересный физический смысл. Оно равно наибольшему числу независимых циклов в графе. При расчёте электрических цепей цикломатическим числом можно пользоваться для определения числа независимых контуров.

Хроматическое число. Пусть р- натуральное число. Граф G называют р-хроматическим, если его вершины можно раскрасить р различными цветами так, чтобы никакие две смежные вершины не были раскрашены одинаково. Наименьшее число р, при котором граф является р-хроматическим, называют хроматическим числом графа и обозначают y(G).

Если y(G)=2, то граф называют называют бихроматическим. Необходимым и достаточным условием того, чтобы граф был бихроматическим, является отсутствие в нём циклов нечётной длины. Хроматическое число играет важную при решении задачи наиболее экономического использования ячеек памяти при программировании. Однако его определение, за исключением случая бихроматического графа, представляет собой довольно трудную задачу, требующую нередко применения электронных вычислительных машин.

Пусть G – связный неориентированный граф, V и V – любые две его вершины. Тогда существует связывающая их простая цепь. М (L1,L2,…,Lq). Если количество ребер q этой цепи не минимальное из возможных , то существует цепь M( L1,L2,…,Lq) , связывающая U и U и имеющая меньшее число ребер. Т.о. существует связывающая U и U цепь М с минимальным количеством ребер р. Минимальная длина простой цепи с началом U и концом U называется расстояние d (U U) между этими вершинами.

Расстояние d(U’ U”) удовлетворяет аксиомам метрики.

1) d(U’ U”) >0 при цепи d(U’ U”) = 0 если U’= U”

2) d(U’ U”) = d (U’ U”)

3) Справедливо неравенство треугольника d(U’ U”)+d(U’ U”) >d(U’ U”).

Диаметр графа

d(G) = max d (U’ U”); U’, U” Î G (2.6)

Пусть V – произвольная вершина графа G. Максимальным удалением в графе G от вершины U называется величина (U) = max d(U U’) U’ G

Вершина U называется центром графа, если максимальное удаление от нее принимает минимальное значение

P (G) = min p (U’), U’ Î G (2.7)

Максимальное удаление р (G) от центра называется радиусом графа.

Центр не обязательно должен быть единственным.

Например в полном неориентированном графе, в котором любые две различные вершины U’ U” V соединены ребром, радиус равен 1 и любая вершина U V является центром.

Связный граф- все его вершины связаны между собой.

Расчет сетевого графика

Граф, некоторые вершины которого выделенные, называется сетью. Выделенные вершины называются полюсами сети. Например, дерево с корнем можно рассматривать, как однополюсную сеть. Изоморфизмом сетей называется изоморфное отображение их графов, при котором полюса обязательно переходят в полюса (иногда налагается условие, чтобы определенные полюса переходили в определенные).

Вершины, отличные от полюсов, называются внутренними вершинами сети. Ребро, инцидентное хотя бы одному полюсу, называется полюсным ребром. Прочие ребра называются внутренними.

Рассмотрим использование положений теории графов при построении сети сложного комплекса работ или операций.

Всякий намеченный комплекс работ, необходимых для достижения некоторой цели, называют проектом. Да, можно говорить о строительстве нового дома, модернизации оборудования, создании нового устройства. При этом сроки выполнения всего проекта заданные и известные продолжительности отдельных работ или операций, которые входят в состав проекта. Каждая такая операция начинается некоторым событием и заканчивается событием. Обычно исходным событием есть начало операции (роботы), а конечной по отношению к данной операции событием есть окончание этой операции, и возможно, начало новой.

Рассмотрим основные расчетные параметры сетевого графика и формулы для их расчета. Обозначим:

t _p - ранний срок наступления события;

t _n ­- поздний срок наступления события ;

t _{i j­} - время операций ;

i - номер предшествующего события ;

j - номер последующего события ;

R _п - полный резерв времени операции ( i , j ) ;

R - резерв времени события ;

t _{p o} - ранний срок окончания операции ( i , j ) ;

t _{п о} - поздний срок окончания операции ( i , j ) ;

Основные временные параметры сетевого графика с детерминированным временем выполнения операций рассчитываются по следующим формулам :

1) ранний срок наступления события j

æ t ⁱ _p + t _{i j} , если к событию j подходит одна

t ^j _p = í операция (2.9)

è max {t ⁱ _p + t _{i j}}, если к событию j подходит

{i} несколько операций;

2) поздний срок наступления события j

æ t ^j _п - t _{i j} если от события j отходит одна

t ⁱ _п = í операция ; (2.10)

è min {t ^j _п - t _{i j}}, если от события j отходит

{j} несколько операций

3) резерв времени события

R = t _n - t _p ; (2.11)

4) ранний срок окончания операции ( i , j )

t _{p о} = t _p + t _{i j ,} при t _{p o} = 0 (2.12)

5) поздний срок окончания операции ( i , j )

t _{n о} = t _n (2.13)

6) полный резерв времени операции ( i , j )

R _n = T_n - T_p - t _{i j} ; (2.14)

где R _n - максимальное время, на которое можно отсрочить или увеличить продолжительность работы ( i , j ), не изменяя директивного или раннего срока наступления завершающего события; R _п принимают минимальные значения для операций, лежащих на критическом пути; эти минимальные значения равны нулю, если директивный срок наступления завершающего события не задан или превышает начало выполнения операций на время, равное продолжительности критического пути.

Критический путь сетевого графика L_кр - это последовательность операций, продолжительность которых составляет минимальное время выполнения всего комплекса операций. Продолжительность критического пути называют критическим временем T_kp. Критический путь L_kp определяется как последовательностью операций с наименьшим полным резервом.

Расчет t _{p o} и t _p ведется от начала сетевого графика к концу, а расчет t _n и t _{n о} - от конца к началу. При этом для конечного события t _p = t _n .

При расчете временных параметров сетевых графиков с детерминированным временем выполнения операций не учитываются случайные изменения продолжительности операций, которые могутоказывать существенное влияния на срок завершения всего комплекса операций.

Пример. В таблице записаны работы ( i , j ) и время их выполнения t_ij ;

i , j	1, 2	1, 3	2, 3	2, 5	3, 4	3, 6	4, 5	4, 6	4, 7	5, 7	6,7
tij

Начертить сетевой график и найти параметры сетевого графика по событиям и работам.

РЕШЕНИЕ По данным работам i, j строим сетевой график. Событий всего 7, значит рисуем 7 вершин. Надо так расположить вершины, чтобы работы i , j не пересекались.

27

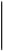2 4 5 2

2 1 29 10

3

2 12 39

7 0

0 15 39

1 0 5 4 2 5

0 17 8

7 8

8 8

3 0 23 31

8 6 0

t _p 31

N R

t _n

Рис. 2.10 - Сетевой график

Находим параметры по событиям.

1) Ранний срок наступления события i, t_p ( i ).Это максимальный путь от начального события до i - го события:

t_p( 1 ) = 0; t_p( 2 ) = t_1,2 = 2

В третье событие входят 2 работы : (2,3) и (1,3), значит

t_p(3)=max{t_p(2) + t_2,3 ; t_p(1) + t_1,3}=max{2+5, 8}= 8

В четвертое событие входит одна работа (3,4)

t_p(4) = t_p(3)+t_3,4 = 8+7=15

В пятое событие входят 2 работы : (2,5) и (4,5), значит

t_p(5)=max{t_p(2) + t_2,5 ; t_p() + t_4,5}=max{2+4, 15+12}= 27

В шестое событие входят две работы : (4,6) и (3,6), значит

t_p(6)=max{t_p(4) + t_2,5 ; t_p(3) + t_3,6}=max{15+4, 8+23}= 31

В седьмое событие входят три работы : (5,7); (4,7); (6,8) значит

t_p(7)=max{t_p(5) + t_5,7 ; t_p(4) + t_4,7; t_p(6) + t_6,7}=

max{5+5, 27+10,31+8}= 39

2) Поздний срок наступления события i, t_n ( i ) — это разность между продолжительностью максимального пути l_max и пути наибольшей продолжительности от данного события i до конечного события.

Рассчитывается t_n ( i ) по обратной схеме t_p ( i ). Значит, расчет начинаем от конечного события, ориентируемся на выходящие работы, берем минимум разности.

Для конечного события

t_n(7) = t_p(7)=39

Из шестого события выходит одна работа : (6,7)

t_n(6) = t_n­­­­­­­_­(7) - t_6,7 = 39 - 8 = 31

Из пятого события выходит одна работа : (5,7)

t_n(5) = t_n­­­­­­­­(7) - t_5,7 = 39 - 10 = 29

Из четвертого события выходит 3 работы : (4,5);(4,6);(4,7)

t_n(4) = min{ t_n­­­­­­­_­(5) - t_4,5 ; t_n­­­­­­­_­(6) - t_4,6 ; t_n­­­­­­­_­(7) - t_4,7 }=

min{29 - 12; 31 - 4; 39 - 5}= 17

Из третьего события выходит 2 работы : (3,4);(3,6)

t_n(3)=min{t_n­­­­­­­_­(4) - t_3,4 ; t_n­­­­­­­_­(6) - t_3,6}=min{17 - 7;31 - 23}= 8

Из второго события выходит 2 работы : (2,5);(2,3)

t_n(2)=min{t_n­­­­­­­_­(5) - t_2,5 ; t_n­­­­­­­_­(3) - t_1,3}=min{8 - 5;29 - 4}= 3

Из начального события выходит 2 работы : (1,2);(1,3)

t_n(1)=min{t_n­­­­­­­_­(2) - t_1,2 ; t_n­­­­­­­_­(3) - t_1,3}=min{3 - 2;8 - 8}= 0

Для начального события должно выполняться условие:

t_p( 1 ) = t_n ( 1 ) = 0 .

3) Находим резерв времени по событиям:

R( i ) = t_n( i ) - t_p( i ).

R(1) = 0; R(2) = 3-2 =1; R(3) = 8-8 = 0;

R(4) = 17-15 = 2; R(5) = 29-27 = 2; R(6) = 31-31 = 0;

R(7) = 39-39 = 0.

4) Критический путь проходит по событиям с нулевым резервом времени R( i ) = 0, т.е. 1, 3, 6, 7, (выделено на графе). Длина критического пути L_кр — это самый длинный путь от начального события до конечного :

L_кр = t_p(7) = 39.

Рассчитаем необходимые параметры по работам.

5) Ранний срок окончания работы ( i , j ) :

t_p.o( i , j )=t_p( i ) + t_i,j

t_p.o(1,2)=t_p(1) + t_1,2 = 0+2 = 2;

t_p.o(1,3)=t_p(1) + t_1,3 = 0+8 = 8;

t_p.o(2,3)=t_p(2) + t_2,3 = 2+5 = 7;

t_p.o(2,5)=t_p(2) + t_2,5 = 2+4 = 6;

t_p.o(3,4)=t_p(3) + t_3,4 = 8+7 = 15;

t_p.o(3,6)=t_p(3) + t_3,6 = 8+23 = 31;

t_p.o(4,5)=t_p(4) + t_4,5 = 15+12 = 27;

t_p.o(4,6)=t_p(4) + t_4,6 = 15+4 = 19;

t_p.o(4,7)=t_p(4) + t_4,7 = 15+5 = 20;

t_p.o(5,7)=t_p(5) + t_5,7 = 27+10 = 37;

t_p.o(6,7)=t_p(6) + t_6,7 = 31+8 = 39;

6) Поздний срок наступления окончания работы ( i , j ):

t_n.o (1,2) = t_n(2) = 3; t_n.o (2,3) = t_n(3) = 8;

t_n.o (1,3) = t_n(3) = 8; t_n.o (2,5) = t_n(5) = 29;

t_n.o (3,4) = t_n(4) = 17; t_n.o (4,5) = t_n(5) = 29;

t_n.o (3,6) = t_n(6) = 31; t_n.o (4,6) = t_n(6) = 31;

t_n.o (5,7) = t_n(7) = 39; t_n.o (4,7) = t_n(7) = 39.

t_n.o (6,7) = t_n(7) = 39;

7) Полный резерв времени работы i , j — это время, на которое можно увеличить продолжительность данной работы, не изменяя при этом продолжительность критического пути L_кр.

R_n( i , j ) = t_n ( j ) - t_p( i ) - - t_i,j;

R_n(1,2) = t_n (2) - t_p(1) - t_1,2 = 3-0-2 = 1;

R_n(1,3) = t_n (3) - t_p(1) - t_1,3 = 8-0-8 = 0;

R_n(2,3) = t_n (3) - t_p(2) - t_2,3 = 8-2-5 = 1;

R_n(2,5) = t_n (5) - t_p(2) - t_2,5 = 8-2-4 = 2;

R_n(3,4) = t_n (4) - t_p(3) - t_3,4 = 17-8-7 = 2;

R_n(3,6) = t_n (6) - t_p(3) - t_3,6 = 31-8-23 = 0;

R_n(4,5) = t_n (5) - t_p(4) - t_4,5 = 29-15-12 = 2;

R_n(4,6) = t_n (6) - t_p(4) - t_4,6 = 31-15-4 = 12;

R_n(5,7) = t_n (7) - t_p(5) - t_5,7 = 39-27-10 = 2;

R_n(6,7) = t_n (7) - t_p(6) - t_6,7 = 39-31-8 = 0;

Работа (4,7) имеет большой резерв времени (12), значит можно с этой работы снять на данном этапе ресурсы и перебросить их на работы лежащие на критическом пути. Аналогично, работы (2,5),(3,4),(4,5),(5,7) имеют резерв времени равный 2 . Работу (2,3) считаем под критической, а работы с нулевым резервом времени — критические. На рисунке критический путь отмечен жирной линией.

2.8. Оптимизация на сетях.

Пусть S - произвольная, частично ориентированная сеть, каждому ребру u которой приписанное неотъемлемое число c(u) - пропускная способность. Потокомв сети S называется пара (f, w), где w - некоторая ориентация всех неориентированных ребер сети, а f(u) -заданная на множестве всех ребер функция с не отрицательными значениями, которые не превосходят пропускных способностей, и такая, что в каждой внутренней вершине a выполняется закон Кірхгофа, соответственно которой сумма значений потока по ребрам, которые входит в вершину, равно сумме потоков по ребрам, которые выходит с вершины . Иными словами, для f(u) выполняются условия:

0 £ f(u) £ c(u) для всех вершин сети;

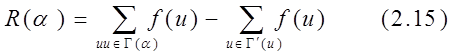R(a) = 0 для всех внутренних вершин, где

а G(a) (соответственно G'(a)) - множество всех ребер, которое выходят из a (соответственно входящих в a) при ориентации w.

Поскольку сумма значений R(a) по всем вершинах сети, включая полюса, равно нулю (каждое ребро есть исходным для одной вершины и входным для другой), то R(a_s) = - R(b_s). Значение R = R(a_s) называется величиной потока.

Рассмотрим задачу определения максимального значения Rmax потока через сеть S при заданных значениях пропускных способностей. Ответ может быть получен в терминах сечений сети.

Сечениемсети называется множество ребер, при удалении которых сеть становится несвязной, причем полюса попадают в разные компоненты связности. В сети на рис.2.11 примерами сечений есть {d, e, f}, {b, c, e, g, h}, {d, g, h, i}.

7 a d h 2

a_S 2 c 4 e 3 g b_S

3 b 4 i

1

f

Рис. 2.11 - Задача максимального потока

Сечение называется простым, если при удалении какого-нибудь его ребра, оно перестает быть сечением. Да, сечения {d, e, f} и {b, c, e, g, h} есть простыми, а сечение {d, g, h, i} не является таким. По-видимому, что для каждого ребра простого сечения можно указать цепь, что проходить через это ребро, но не проходит через иные ребра данного сечения.

Если в связной сети выполняется простое сечение, то сеть распадается ровно на две части: левую часть, что содержит a_S, и правую часть, что содержит b_S. Каждое ребро простого сечения связывает вершины с разных частей. Будем называть ребро сечения прямым, если оно в сети не ориентированное или ориентирован слева по правой сторону, и обратным в противном случае. Будет ориентированное ребро прямым или обратным, зависит от выбора сечения. Так, в примере ребро е в сечениях {d, e, f} и {b, c, e, g, h} - обратное, а в сечении {a, c, e, g, i}- прямое.

Каждому простому сечению W припишем пропускную способность c(W), равную сумме пропускных способностей всех его прямых ребер. В примере на рис.2.11 сечение {d, e, f} имеет пропускную состоятельность 5+1=6, а сечение {b, c, e, g, h} - 3+2+3+2=10.

Теорема о максимальной пропускной состоятельность сети сформулированная Фордом и Фалкерсоном в таком виде: Максимальный размер потока Rmax через сеть S равно минимальной с пропускных способностей c_min ее простых сечений. Доказательство этой теоремы приведено в [2]. Эта теорема положена в основу задачи определения максимальной пропускной состоятельности сети.

I

b t

I

Обозначено: I - ресурсы не использованы

R - ресурсы использованы полностью

IR - ресурсы использованы частично

1. Выбираем какой - то один из произвольных потоков.

p1 = min {f(s, b), f(b, t)} = min {6.2; 8} = 6.2;

I

c e