Тема 3 Дисконтирование
Дисконтирование – это процесс определения современной т.е. текущей стоимости капитала, если известна его будущая стоимость.
Различают математическое и банковское дисконтирование. Банковское дисконтирование осуществляется на основе учетной ставки (d), математическое на основе процентной ставки (I). Дисконтирование осуществляется как по простым, так и по сложным процентам.
Дисконтирование по простым процентам:
Математическое дисконтирование осуществляется по формуле:
| P= | S |
| 1 + n*i |
Банковское дисконтирование осуществляется по формуле:
P = S * ( 1 – n*d).
Пример:Вексель номинальной стоимостью 500000 рублей был учтен в банке за 90 дней до срока погашения по учетной ставке 16% годовых. Определить дисконтированную величину векселя, при продолжительности года 360 дней..
Решение: Р = 500000 ( 1 – 90/360 * 0,16 ) = 480000.
Ответ: 480000 рублей.
Дисконтирование по сложным процентам:
Математическое дисконтирование осуществляется по формуле:
| P= | S | |
| n | ||
| (1 + i) |
Банковское дисконтирование осуществляется по формуле:
| P =S ( 1 - d) | n |
Пример:Владелец долгового обязательства номинальной стоимостью 6000000 рублей со сроком погашения 2 года, сразу же после заключения договора учел его в банке по сложной ставке 9% годовых. Определить дисконтированную величину долгового обязательства, если проценты начисляются ежеквартально.
Решение:
| P =6000000 *( 1 - | 0,09 | ) | 4*2 | ,=5001326,40 |
Ответ: 5001326 рублей 40 копеек
(2,тема.1, §1.3; с14-21);
Тема 4 Инфляция
Для количественной оценки инфляции используют такие показатели как уровень инфляции (r) и индекс инфляции (U).
Уровень инфляции показывает на сколько процентов выросли цены за рассматриваемый период времени.
| r= | S(1) - S (0) |
| S(0) |
r - уровень инфляции;
S(0) – цена товара на начало рассматриваемого периода;
S (1) - цена товара на конец рассматриваемого периода.
Для определения во сколько раз в среднем за рассматриваемый период выросли цены рассчитывается индекс инфляции.
U = 1 + r.
Если известен уровень инфляции за определенный период в течении срока сделки, то индекс инфляции можно найти по формуле:
| U = (1 + r) | n |
n – количество изменений уровня инфляции в течении срока сделки.
Определим формулы различных процентных ставок с учетом инфляции при применении простых процентов.
Процентная ставка с учетом инфляции:
| I ( r ) = | (1 + n*I )* U - 1 |
| n |
Учетная ставка с учетом инфляции:
| d ( r ) = | U - 1 + n*d |
| U * n |
Определим формулы различных процентных ставок с учетом инфляции при применении сложных процентов.
Процентная ставка с учетом инфляции
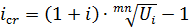
Учетная ставка с учетом инфляции
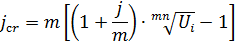
Номинальная процентная ставка с учетом инфляции
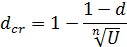
Пример: Кредит в размере 50000 рублей выдан на 2 года. Реальная доходность операции составляет 10 % годовых. Ожидаемый уровень инфляции составляет 15% в год. Определить процентную ставку учитывающую инфляцию по простым процентам и сумму накопленного долга.
Решение: Определим индекс инфляции за весь срок сделки:
| U = (1 + 0,15) | ,=1,32 | |
Определим процентную ставку учитывающую инфляцию:
| I (r) = | (1 + 2 * 0,1) * 1,15 - 1 | ,=0,19 |
Процентная ставка учитывающая инфляцию составляет 19% годовых.
Найдем наращенную сумму с учетом инфляции:
S (r) = 50000 (1 + 2 * 0,19 ) = 69000.
Ответ: 69000 рублей
(2,тема.2, §2.3; с30-35);
