Тема 5 Потоки платежей. Финансовые ренты

Поток платежей все члены которого положительные величины, а временные интервалы между платежами одинаковы называют финансовой рентой или аннуитетом.

Обобщающими характеристиками финансовой ренты являются:

- наращенная сумма (S) – сумма всех членов потока платежей с начисленными на них процентами на конец срока, то есть на дату последней выплаты;

- современная величина (А) (современная стоимость, капитализированная стоимость) – это сумма всех членов потока, дисконтированных на определенный момент времени, совпадающий с началом потока или предшествующий ему. Современная величина показывает какую сумму следовало бы иметь на этот момент, что бы при начислении установленных процентов на момент окончания ренты получить наращенную сумму.

- размер платежа финансовой ренты (R) – сумма всех внесенных платежей в течении года, одним или несколькими платежами

Различают два вида финансовых рент: рента постнумерандо - платежи осуществляются в конце периода, рента пренумерандо - платежи осуществляются в начале периода.

Величина финансовой ренты зависит от количества платежей в году (Р) и от количества начислений процентов в году (m).

Формулы для расчета наращенной суммы ренты постнумерандо:

Р=1; m=1

		n
S = R	(1+i)	-1
	i

Р=1; m 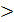1

Р 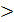1; m=1

		n
S = R/P	(1+i)	-1
	1/p
	( 1 + i)	-1

Р 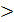1; m= р

		n* m
S = R	(1+ j / m )	-1
j

Р 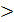1; m=/=1

		n* m
S = R/ P	(1+ j / m )	-1
	m/p
	(1 + j/m)	-1

Формулы для расчета современной величины ренты постнумерандо:

Р=1; m=1

		n
A = R	(1+i)	-1
	i

Р=1; m 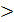1

		n*m
A = R	(1+ j / m )	-1
	m
	( 1 + j / m)	-1

Р 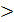1; m=1

		n
A = R/P	(1+i)	-1
	1/p
	( 1 + i)	-1

Р 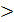1; m= р

		n* m
A = R	(1+ j / m )	-1
j

Р 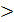1; m =\=1

		n* m
A = R/ P	(1+ j / m )	-1
	m/p
	(1 + j/m)	-1

Пример: В инвестиционный фонд в течении 3-х лет вносится в конце по 100000 рублей. На взносы начисляются сложные проценты по ставке 12% годовых. Определить размер инвестиционного фонда если взносы осуществляются один раз в год, а проценты начисляются ежеквартально.

Решение: Необходимо определить формулу для проведения расчета для нахождения размера инвестиционного фонда (S).Для этого определяем дополнительные данные: взносы осуществляются один раз в год ( Р = 1), проценты начисляются ежеквартально (m = 4 ). Этим параметрам удовлетворяет следующая формула:

		n*m
S = R	(1+ j / m )	-1
	m
	( 1 + j / m)	-1

		3*4
S = 100000	(1+ 0,12 / 4 )	-1
	(1+0,12 / 4)	-1

Ответ: 330769 рублей 23 копейки

Формулы для расчета ренты пренумерандо изучите самостоятельно.

(2,тема.4, §4.1- 4.4; с57-70);

Тема 6 Эквивалентные процентные ставки

Эквивалентные ставки, это ставки которые приводят в конкретных условиях к одинаковым финансовым результатам. Формулы эквивалентных ставок выражают из множителей наращения. Эквивалентные ставки существуют как при начислении простых, так и сложных процентов. Существуют следующие пары эквивалентных ставок:

I (п) - d (п)	I (п) - I (c)	I (п) - d (c)	I (п) - j (c)
d (п) - d (c)	d (п) - i (c)	d (п) - j (c)	I (c) - d (c)
I (c) – j (c)	d (c) - j (c)

(2,тема.3, §3.1-3.2; с41-47);