Эквивалентность во времени денежных сумм. Текущая стоимость денег

Рыночная экономика предоставляет предприятиям, осуществляющим производственную деятельность, возможность размещать свои временно свободные денежные средства на условиях срочности, платности, возвратности с целью:

1) получения процентного или дисконтного, а также курсового дохода;

2) сохранения денежных средств от инфляционного обесценения.

Основными характеристиками любого объекта инвестирования являются:

1) первоначально размещаемая (исходная, номинальная) сумма денежных средств (PV);

2) доход в процентном выражении (процентная ставка — г или ставка дисконта — d);

3) единичный промежуток (стандартный интервал) начисления дохода;

4) возвращаемая сумма (сумма погашения) (FV).

В зависимости от того, какие заданы характеристики, изменяются направления движения денежных потоков, генерируемых инвестицией.

Процесс инвестирования, в котором заданы исходная (номинальная) сумма (PV) и процентная ставка (r), называется процессом наращения. Возвращаемая сумма (сумма погашения) называется наращенной суммой (FV). Доход представляет собой разницу между возвращаемой и номинальной суммой. Доходность операции характеризует процентная ставка (процент).

Формула наращения имеет следующий вид:

PV + r • PV = FV;

FV = PV + r • PV;

FV = PV (1 + r).

Процесс инвестирования, в котором заданы возвращаемая сумма (сумма погашения) (FV) и дисконтная ставка (d), называется процессом математического дисконтирования. При этом возвращаемая сумма (сумма погашения) (FV) равна номинальной сумме объекта вложения денежных средств, а исходная сумма (PV) — меньше номинальной. Инвестируемая сумма в данном случае называется приведенной суммой. Доходность операции характеризует дисконтная ставка (дисконт).

Формула математического дисконтирования имеет следующий вид:

PV = FV (1 — d).

Так как процесс дисконтирования является обратным процессу наращения, формула дисконтирования является результатом преобразования формулы наращения:

PV + d • FV = FV;

PV = FV - d • FV;

PV = FV (1 - d).

От математического дисконтирования следует отличать так называемое банковское дисконтирование, под которым понимается поиск исходной суммы для наращения заданной суммы по заданной процентной ставке. Формула (банковского) дисконтирования имеет следующий вид:

PV = FV/(1 + r).

Формула банковского дисконтирования является результатом преобразования формулы наращения:

PV + r • PV = FV;

PV (1+ r) = FV;

PV = FV/(1 + r).

Применительно к банковскому дисконтированию говорят о дисконтировании по простой или сложной ставке процентов. Взаимосвязь процентной и дисконтной ставки. Процентная ставка, характеризующая доход при наращении, и дисконтная ставка, характеризующая доход при дисконтировании, являются взаимосвязанными и взаимозависимыми. Если известна процентная ставка, можно рассчитать дисконтную ставку, и наоборот.

Из формулы операции наращения (FV = PV + r • PV) следует формула определения процентной ставки:

r • РV = FV — PV;

r = (FV — PV)/PV.

Из формулы операции дисконтирования (PV = FV — d • FV) следует формула определения дисконтной ставки:

d • FV - FV - PV;

d = (FV - PV) / FV.

Процентную ставку можно выразить через дисконтную ставку. Если

r • PV = FV — PV;

PV = FV — d • FV,

то

r • (FV — d • FV) = FV — (FV — d • FV);

r • FV (1 - d) - FV - FV + d • FV;

r • FV (1 - d) = d • FV; r • (1 - d) = d.

r = d/(l-d)

Дисконтную ставку, в свою очередь, можно выразить через процентную ставку. Если

d • FV = FV - PV;

FV = PV (1 + r),

то

d • PV (1 + r) = PV (1 + r) - PV;

d • PV (1 + r) = PV + PV • r - PV;

d • PV (1 + r) = PV • r; d • (1 + r) = r.

d = r/(l+r)

Мультиплицирующие и дисконтирующие множители. Для облегчения расчетов наращенных и дисконтированных сумм составлены таблицы, соответственно, мультиплицирующих и дисконтирующих множителей.

Мультиплицирующий множитель FM1(n, r) показывает, во сколько раз увеличится сумма, вложенная на n лет под r процентов годовых, т.е. характеризует будущую стоимость одной денежной единицы на конец периода n:

FM1(n, r) = (1 + r )n.

Дисконтирующий множитель FM2 (n, r) показывает, какую долю от наращенной суммы составит начальная сумма, вложенная на n лет под r процентов годовых к концу n-го года, т.е. характеризует приведенную стоимость одной денежной единицы, ожидаемой к получению через л периодов:

FM2 (n, r) = 1 / FM (n, r) = 1 / (1 + r )n = (1 + r)-n.

Величина FM (n, r) в случае дисконтирующего множителя называется приведенной (текущей, временной) стоимостью одной денежной единицы, вложенной на n лет под r процентов годовых. С помощью данной величины можно привести в соответствие вложенную и возвращаемую суммы.

Мультиплицирующий и дисконтирующий множители можно рассчитать для срочного аннуитета постнумерандо в одну денежную единицу продолжительностью n периодов.

Мультиплицирующий множитель FM3(n, r) характеризует будущую стоимость срочного аннуитета постнумерандо в одну денежную единицу продолжительностью n периодов:

Дисконтирующий множитель FM4 (n, r) характеризует приведенную стоимость срочного аннуитета постнумерандо в одну денежную единицу продолжительностью n периодов:

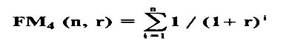
Банковской практике существуют различные способы определения срока вложения денежных средств при начислении процентного (дисконтного) дохода. Представление о трех наиболее применяемых практиках (немецкой, французской, английской) наглядно иллюстрирует таблица.

Практика определения расчетного количества дней в финансовых периодах

Название банковских практик	Расчетное количество дней
в (финансовом) месяце	в (финансовом) году
Немецкая
Французская	По календарю
Английская	По календарю	По календарю

В зависимости от применяемой практики расчета количества дней в финансовом месяце и финансовом году различают точные и обыкновенные процентные (или дисконтные) ставки.

Точные проценты (дисконты) рассчитываются, исходя из точного количества дней в календарном месяце и календарном году.

Обыкновенные проценты (дисконты) рассчитываются, исходя из приблизительного (округленного) количества дней в месяце и году.

Простые и сложные проценты

Наращение может осуществляться по схеме простых и сложных процентов.

Формула наращения простых процентов (simple interest). Наращение простых процентов означает, что инвестируемая сумма ежегодно возрастает на величину PV • r. В этом случае размер инвестированного капитала через n лет можно определить по формуле:

FV = PV (1 + r • n).

Формула наращения сложных процентов (compound interest). Наращение по схеме сложных процентов означает, что очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также ранее начисленные и не востребованные инвестором проценты. В этом случае размер инвестированного капитала через n лет можно определить по формуле:

FV = PV (1 + r)n.

При одном и том же значении процентной ставки:

1) темпы наращения сложных процентов выше темпов наращения простых, если период наращения превышает стандартный интервал начисления дохода;

2) темпы наращения сложных процентов меньше темпов наращения простых, если период наращения меньше стандартного интервала начисления дохода.

Области применения простых и сложных процентов. Простые и сложные проценты могут применяться как в отдельных операциях, так и одновременно. Области применения простых и сложных процентов можно разделить на три группы:

1) операции с применением простых процентов;

2) операции с применением сложных процентов;

3) операции с одновременным применением простых и сложных процентов.

Областью применения простых процентов чаще всего являются краткосрочные операции (со сроком до одного года) с однократным начислением процентов (краткосрочные ссуды, вексельные кредиты) и реже — долгосрочные операции.

При краткосрочных операциях используется так называемая промежуточная процентная ставка, под которой понимается годовая процентная ставка, приведенная к сроку вложения денежных средств. Математически промежуточная процентная ставка равна доле годовой процентной ставки. Формула наращения простых процентов с использованием промежуточной процентной ставки имеет следующий вид:

FV = PV (1 + f • r),

или

FV = PV (1 + t • r / Т),

где f=t/T;

t — срок вложения денежных средств (при этом день вложения и день изъятия денежных средств принимаются за один день); Т — расчетное количество дней в году.

При долгосрочных операциях начисление простых процентов рассчитывается по формуле:

FV = PV (1 + r • n),

где n — срок вложения денежных средств (в годах). ,

Областью применения сложных процентов являются долгосрочные операции ( со сроком, превышающим год), в том числе предполагающие внутригодовое начисление процентов.

В первом случае применяется обычная формула начисления сложных процентов:

FV = PV (1 + r)n.

Во втором случае применяется формула начисления сложных процентов с учетом внутригодового начисления. Под внутригодовым начислением процентов понимается выплата процентного дохода более одного раза в год. В зависимости от количества выплат дохода в год (m) внутригодовое начисление может быть:

1) полугодовым (m = 2);

2) поквартальным (m = 4);

3) ежемесячным (m = 12);

4) ежедневным (m = 365 или 366);

5) непрерывным (m -» ?).

Формула наращения при полугодовом, поквартальном, ежемесячном и ежедневном начислении сложных процентов имеет следующий вид:

FV = PV (1 + r / m)nm,

где PV — исходная сумма;

г — годовая процентная ставка;

n — количество лет;

m — количество внутригодовых начислений;

FV — наращенная сумма.

Номинальная процентная ставка задается изначально. Для каждой номинальной процентной ставки и на ее основании можно рассчитать эффективную процентную ставку (rе).

Из формулы наращения сложных процентов можно получить формулу эффективной процентной ставки:

FV = PV (1 + r)n;

(1 + re) = FV / PV.

Приведем формулу наращения сложных процентов с внутригодовыми начислениями, при которых каждый год начисляется r / m процента:

FV = PV (1 + r / m)nm.

Тогда эффективная процентная ставка находится по формуле:

(1 + re) = (1 + r/m)m,

или

re = (l + r/m)m- 1,

где rе — эффективная процентная ставка; r — номинальная процентная ставка; m — количество внутригодовых выплат.

Величина эффективной процентной ставки зависит от количества внутригодовых начислений (m):

1) при m = 1 номинальная и эффективная процентные ставки равны;

2) чем больше количество внутригодовых начислений (значение m), тем больше эффективная процентная ставка.

Областью одновременного применения простых и сложных процентов являются долгосрочные операции, срок которых составляет дробное количество лет. При этом начисление процентов возможно двумя способами:

1) начисление сложных процентов с дробным числом лет;

2) начисление процентов по смешанной схеме.

В первом случае для расчетов применяется формула сложных процентов, в которой присутствует возведение в дробную степень:

FV = PV (1 + r)n+f,

где f — дробная часть срока вложения денежных средств.

Во втором случае для расчетов применяется так называемая смешанная схема, которая включает формулу начисления сложных процентов с целым числом лет и формулу начисления простых процентов для краткосрочных операций:

FV = PV (1 + r)n • (1 + f • r),

или

FV = PV (1 + r)n • (1 + t • r / Т).

Процентный доход при непрерывном начислении процентов рассчитывается по следующей формуле:

FVn = Р • ern,

или:

FVn = P • e?n,

где: e = 2, 718281 — трансцендентное число (число Эйлера);

е?n — множитель наращения, который используется как при целом, так и дробном значении n;

? — специальное обозначение процентной ставки при непрерывном начислении процентов (непрерывная процентная ставка, «сила роста»);

n — количество лет.

При одинаковой величине исходной суммы, одинаковом сроке вложения денежных средств и значении процентной ставки возвращаемая сумма оказывается больше в случае использования формулы внутригодовых начислений, чем в случае использования обычной формулы начисления сложных процентов:

FV = PV (1 + r / m)nm > FV = PV (1 + r)n.

Если доход, полученный при использовании внутригодовых начислений, выразить в процентах, то полученная процентная ставка окажется выше той, которая использовалась при обычном начислении сложных процентов.

Таким образом, первоначально заявленная годовая процентная ставка для начисления сложных процентов, называемая номинальной, не отражаетреальной эффективности сделки. Процентная ставка, отражающая фактически полученный доход, называется эффективной.

Денежные суммы PV(T) в момент времени Т и РV1 (t) в момент времени t называются эквивалентными по ставке сравнения г, если:

PV(T) = PV1 (t) • (1 + r)T - t.

Приведенная формула сравнения денежных сумм в любые моменты времени называется математическим дисконтированием.

При Т > t это означает, что сумма PV1(t), наращенная по ставке г сложных процентов, превратится в момент Т в сумму PV(T). При Т < t это означает, что сумма PV(T), наращенная по ставке г сложных процентов, превратится в момент t в сумму PV1(t). Таким образом, приведенная выше формула учитывает оба случая изменения денежных сумм во времени. Другими словами, при Т > t эквивалентность сумм PV(T) и PV1(t) означает, что сумма PV(T), уменьшающаяся при движении в прошлое за каждый единичный промежуток времени в [1 / (1 + r)] раз, к моменту времени t превратится в сумму, равную PV1(t):

PV1(t) = PV(T) / (1 + r)T - t

Данная формула представляет собой приведение будущей суммы к настоящему моменту времени.

Текущая (временная) стоимость денег

Размещая денежные средства в доходные активы, предприятие рассчитывает не только вернуть вложенную сумму, но и получить прибыль. На практике сумма возврата может отличаться от вложенной суммы следующим образом:

1) стать больше вложенной суммы, что означает получение дохода;

2) остаться равной вложенной сумме, что означает только возврат инвестируемых средств без получения дохода;

3) стать меньше вложенной суммы, что означает прямой убыток.

Если денежные средства не размещаются на условиях срочности, платности, возвратности, а «лежат мертвым грузом», то все равно со временем обесцениваются от инфляции. Таким образом, стоимость денег изменяется со временем. Измененная во времени стоимость денег называется временной или текущей стоимостью. Одной из главных задач инвестора является определение той суммы, которой он будет располагать по окончании срока размещения денежных средств. Математическая запись кредитной (инвестиционной) операции позволяет определить сумму, которой будет располагать кредитор (инвестор) по окончании срока размещения средств:

FV = PV + r • PV;

FV = PV (1 + r).

Преобразуем формулу кредитной (инвестиционной) операции следующим образом:

PV (1 + r) = FV;

PV = FV / (1 + r);

PV = FV • 1 / (1 + r).

В результате преобразования получена формула текущей (приведенной) стоимости, выражающая стоимость размещаемых денежных средств через будущие поступления (FV) при заданной норме доходности.

Норма доходности не является постоянной величиной и зависит от риска, связанного с вложением денежных средств. Между риском и нормой доходности существует прямая зависимость:

1) чем выше риск вложений, тем больше норма доходности;

2) чем меньше риск вложений, тем меньше норма доходности.

Выражение 1 / (1 + r) называется коэффициентом дисконтирования. Коэффициент дисконтирования приводит ежегодный доход, который кредитор (инвестор) может получить от размещения своих денежных средств, к настоящему времени.