Зависимость между доходом по портфелю и вероятностью его получения

Портфель I	Рі	0,1	0,2	0,4	0,2	0,1
	Ri, тыс. ден. ед.
Портфель II	Рі	0,1	0,2	0,4	0,2	0,1
	Ri, тыс. ден. ед.

Средний ожидаемый доход по портфелям І и II в соответствии с (1.16) равняется:

M(R_I) = 0,1 × 85 + 0,2 × 95 + 0,4 × 100 + 0,2 × 105 + 0,1 × 115 = 100 тыс. ден. ед.

M(R_II) = 0,1 × 75 + 0,2 × 90 + 0,4 × 100 + 0,2 × 110 + 0,1 × 125 = 100 тыс. ден. ед.

Функциональные зависимости между величинами R_i, и их вероятностями Р_i называют кривыми распределения вероятностей. Если эти зависимости имеют вид, как показано на рис. 5, соответствующее распределение называют нормальным. Это распределение имеет очень широкое практическое применение как в математике, так и в экономике и непосредственно в финансах. С достаточной степенью точности можно считать, что зависимость между возможной величиной дохода и соответствующей вероятностью в этом примере и многих других прикладных задачах подчиняется нормальному закону.

Тем не менее, не во всех случаях такая аппроксимация вероятностей является приемлемой. Например, в случае досрочного погашения займа или облигации, выполнение американского опциона или варранта, конвертации облигации в акцию существует неопределенность, связанная с возможностью выбора того ли другого варианта, которая вызовет асимметрию в распределении вероятностей. Присутствие такой асимметрии усложняет оценивание соответствующих рисков и управления ими. Итак, оценивание рисков в большинстве случаев проводится на основании очень удобного в использовании нормального распределения вероятностей, а в случае потребности риски оцениваются по более сложной методике на основании асимметрического распределения вероятностей.

Определим риск в сроках теории вероятности, а именно, какая вероятность получить доход меньше ожидаемого. Степень риска целесообразно измерять такой вероятностной характеристикой, как стандартное отклонение, которое определяют по формуле

. (17)

Для нормального распределения выполняется так называемое правило «3s», которое имеет очень важное практическое применение в теории риска, а именно вероятность того, что величина среднего ожидаемого дохода M(R) находится в интервале [M(R) – 3s, M(R) + 3s] и равняется 0,997, то есть почти 1. Это означает, что если известная величина s, можно почти беспрекословно утверждать, что ожидаемый доход находится в интервале [M(R) – 3s, M(R) + 3s], или [R_min, R_max]. Вероятность того, что ожидаемый доход M(R) находится в интервале [M(R) – s, M(R) + s], равняется 0,68, а та, что в интервале [M(R) – 2s, M(R) + 2s], – 0,95.

Итак, величина s дает возможность оценить степень неопределенности или, другими словами, указать интервал неопределенности величины ожидаемого дохода, то есть оценить риск (см. рис. 6).

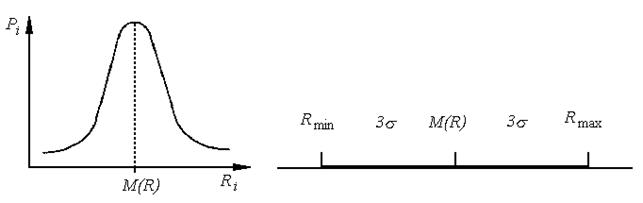
Рис. 5. Нормальное распределение вероятностей

Рис. 6. Интервал неопределенности величины ожидаемого дохода

Чем больше величина s в каждом конкретном случае, тем больше интервал неопределенности и риск.

Определим по формуле (1.17) стандартное отклонение для портфелей І і II, тыс. ден. ед.:

s₁ = [0,1 (85 – 100)² + 0,2 (95 – 100)² + 0,4 (100 – 100)² + 0,2 (105 – 100)² + 0,1 (115 – 100)²]^1/2 = 7,42;

s₂ = [0,1 (75 – 100)² + 0,2 (90 – 100)² + 0,4 (100 – 100)² + 0,2 (110 – 100)² + 0,1 (125 – 100)²]^1/2 = 12,85.

Полученные результаты свидетельствуют о том, что портфель II является более рискованным, чем портфель І, хотя ожидаемый доход по портфелю І равняется ожидаемому доходу по портфелю II.

Стандартное отклонение является абсолютным показателем непостоянства ожидаемого дохода. Относительным показателем непостоянства ожидаемого дохода является коэффициент вариации, который определяют по формуле

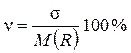. (18)

Этот показатель также отражает риск и измеряется в процентах к величине ожидаемого дохода. Значение n < 10% отражает слабое изменение, 10% < n < 25% – среднее и n > 25% – высокое изменение.

В таблицы 2 приведены средние значения коэффициентов вариации для некоторых видов ценных бумаг США за период с 1926 по 1981 г.

Таблица 2