Построение прогнозной модели изменения запасов и выручки на предприятии с помощью регрессионного анализа

Если предположить, что отношение между определенным типом активов и выручкой является линейным, то можно воспользоваться простой линейной регрессией для оценки потребности фирмы в этих активах при любом заранее заданном приросте уровня выручки.

Регрессионный анализ – это метод установления аналитического выражения стохастической зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем изменяется у при изменении любого х. Применяется регрессионный анализ главным образом для планирования, а также для разработки нормативной базы. Он отвечает на вопрос, существует ли связь между анализируемыми признаками и дает ее формализованное выражение, он показывает одностороннюю зависимость, то есть связь, показывающую, каким образом изменение факторных признаков влияет на признак результативный. [44, стр. 206]

Поскольку, из ранее сделанных выводов, известно, что запасы на предприятии за рассматриваемые три года достаточно выросли и их темп прироста составил 3208%, то целесообразно провести анализ взаимосвязи запасов и выручки на предприятии, а также спрогнозировать на 2009 год размер запасов и выручки. В приложении А представлен расчет линейной регрессии.

Линейное уравнение регрессии имеет следующий вид: [44, стр. 207]

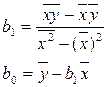
у = b₀ + b₁ ,где

Исходя из расчетов, представленных в приложении А, линейное уравнение регрессии примет вид: у = 591,32 + 0,322x.

Индекс b₁ = 0,3215807 говорит нам о том, что при увеличении выручки от реализации продукции на 1 ед. запасы увеличиваются на 0,3215807. Рассчитываем коэффициент корреляции по следующей формуле: [44, стр. 208]

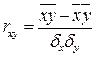, где

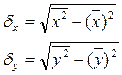
Коэффициент корреляции равен 0,6203307. Значит можно сделать вывод, что между х и у, то есть между выручкой и запасами связь не тесная.

Рассчитаем коэффициент детерминации: [44, стр. 209]

D = r²_xy * 100

D = 38,48 (%)

Следовательно, величина запасов только на 38,48% объясняется величиной выручки от реализации продукции.

Рассчитаем дисперсионное отношение Фишера: [44, стр. 210]

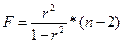, где n – число периодов

Следовательно, n = 12.

F _{расчетное} = 17,51440376.

Найдем F_{табличное}: k₁ = m, m = 1(т.к. на y влияет только один фактор х),

k₂ = n- m-1. Значит k₁ = 1, k₂ = 12-1-1= 10. Находим табличное значение F на пересечении k₁ и k_2. Получаем, что F_{табличное} = 4,96. Так как F_{расчетное} > F_{табличное} значит уравнение статистически значимо.

Рассчитаем стандартные ошибки коэффициентов регрессии: [44, стр. 211]

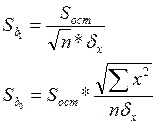, где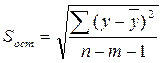

При вычислении S_ост было получено, что S_ост = 1071,77. Следовательно,

S_b1 = 0,0486, S_b0 = 251,159. Рассчитав стандартные ошибки коэффициентов регрессии, можно рассчитать доверительные интервалы: [44, стр. 211]

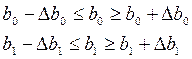, где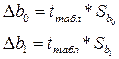

t_табл находится по таблице t-критерия Стюдента при уровне значимости 0,05 и числе степенной свободы равной 14. Следовательно, можно рассчитать доверительные границы коэффициентов регрессии:

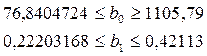
Значит можно сделать вывод, что коэффициенты b₁ и b₀ значимы, так как они лежат в этих интервалах, то есть модель адекватна.

Рассчитаем t – статистики Стюдента: [44, стр. 212]

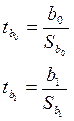
Получается, что 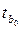= 2,354, 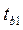= 6,6171. Значит коэффициенты b₁ и b₀ значимы, так как они оба больше t_табл, следовательно, оба коэффициента оказывают воздействие на результативный признак, то есть на запасы предприятия.

Рассчитаем индекс корреляции: [44, стр. 213]

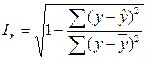
В результате получаем, что I_r = 0,77036 = r_xy. Следовательно, индекс корреляции и коэффициент корреляции рассчитаны верно и оба они показывают, что связь между запасами и выручкой на предприятии не тесная.

Рассчитаем значение коэффициента эластичности: [44, стр. 214]

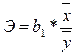
В результате Э = 0,7945345. Коэффициент эластичности показывает, что на 0,79% изменится результат запасов (у) при изменении на 1% выручки от реализации продукции (х).

Теперь возможно оценить качество модели с помощью коэффициента аппроксимации: [44, стр. 215]

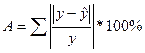
В результате получаем, что А = 41,52, следовательно, коэффициент аппроксимации не принадлежит интервалу [0,7;1]. Значит можно сделать вывод о том, что модель не качественная.

Таким образом, можно проиллюстрировать линейную регрессионную модель (рисунок 1).

Величина запасов на предприятии только на 39% объясняется величиной выручки от реализации продукции. Из рисунка видно, что нанесенные точки лежат достаточно далеко от линии тренда, это означает, что на изменение запасов достаточно влияют факторы, отличные то изменения выручки от реализации продукции.

Так же возможно рассчитать степенную регрессионную модель (Приложение Б). Ее результаты подтверждают выводы сделанные при линейной регрессионной модели. Однако когда, мы строим линию тренда степенной регрессионной модели (рисунок 1), то видно, что в степенной регрессионной модели теоретическая прямая достаточно отклоняется от прямой в линейной регрессионной модели. Так же можно наглядно увидеть, что наибольшая концентрация «наших значений» наблюдается при выручке равной от 6000 до 8000 и запасов равных от 5050 до 5550, т.е. на этом промежутке происходит наибольшее пересечение выручки от реализации продукции с запасами на производстве.

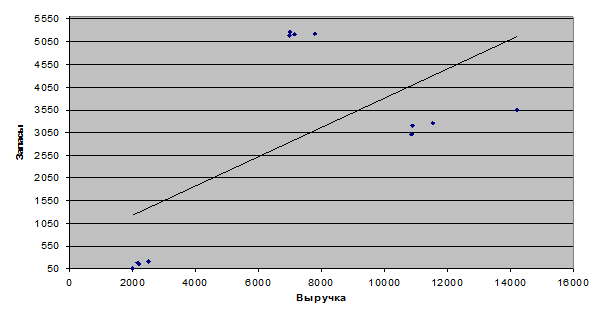
Рисунок 1 – Линейная регрессионная модель

Источник: Составлено автором.

Так же концентрация значений происходит в промежутках по выручке от 10000 до 12000, а по запасам от 3000 до 3500.

Если учесть, что предприятие работает в условиях существующего кризиса, то если оно в 2009 году вновь увеличит величину своих запасов (при неизменности объемов изготавливаемой продукции, снижающейся выручке и неспособности быстро и с выгодой для себя реализовывать имеющиеся запасы), это негативно скажется на выручке от реализации, повлечет за собой расходы по хранению и содержанию данных запасов.

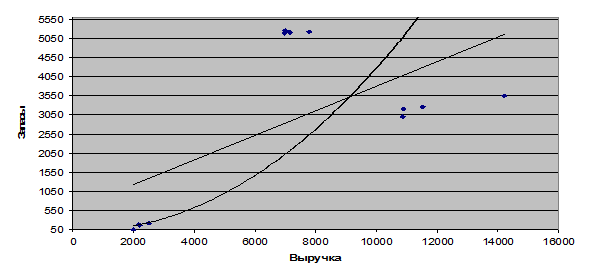
Рисунок 2 – Степенная регрессионная модель

Источник: Составлено автором.