Далее материал только для ознакомления

Задача 2.

Исходные данные о доходности ценных бумаг. Определить доли акций в портфеле при условии, что: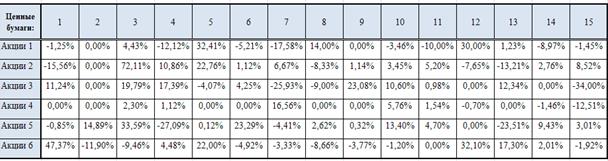

Прямая задача: доходность стремится к максимуму, а риск ограничен 8%,

Обратная задача: риск стремится к минимуму, а доходность не должно быть ниже 4 %

Решение:

1.Определим доходность и риск рассматриваемых ценных бумаг

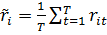
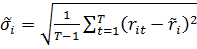
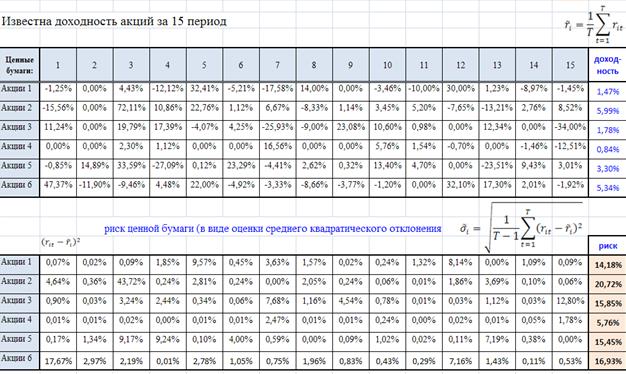
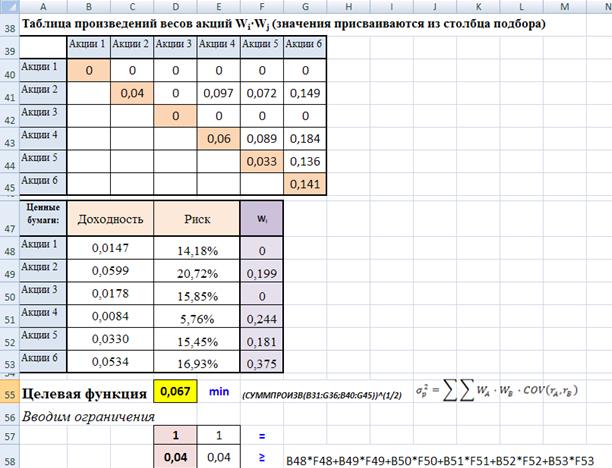
2. Найдем таблицу коэффициентов ковариации

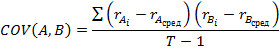
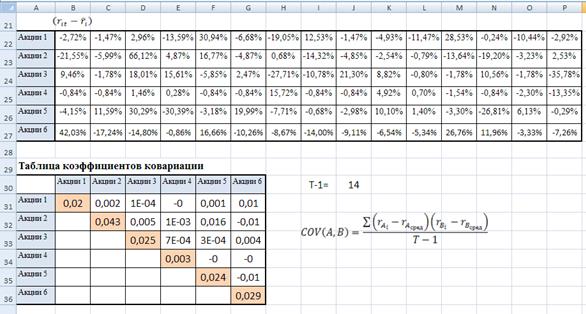
3. Подготовим таблицу для линейной оптимизации

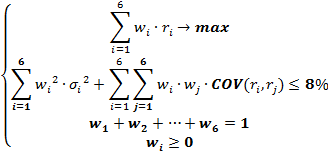
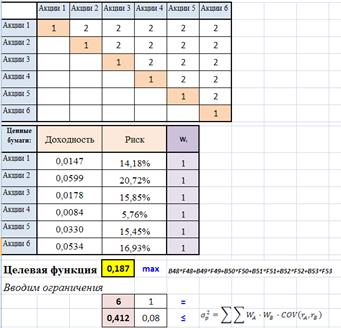Таблица произведений весов акций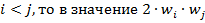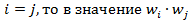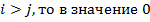

Применим «Поиск решения»

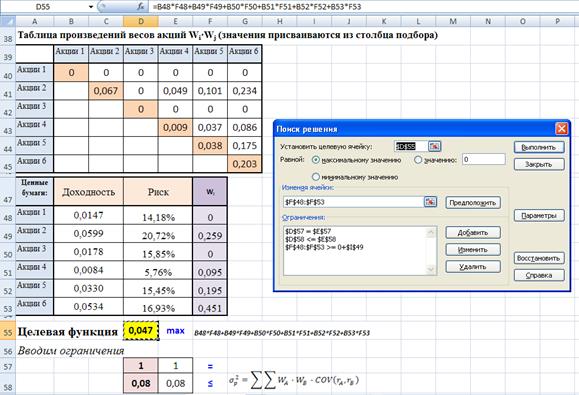
Обратная задачи по оптимизации фондового портфеля.

Риск стремится к минимуму, а доходность не должна быть ниже 4 %

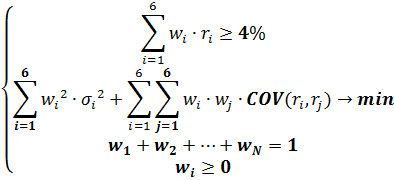
Таким образом, получены оптимальные решения для прямой и обратной задач

	Структура портфеля
	Прямая задача	Обратная задача
Требования:	Риск меньше 8%	Доходность выше 4%
Акции 1	0%	0%
Акции 2	26%	20%
Акции 3	0%	0%
Акции 4	10%	24%
Акции 5	19%	18%
Акции 6	45%	38%
Характеристики	Доходность 4.68%	Доходность 4%
оптимального портфеля	Риск 8%	Риск 6.65%

Основной недостаток модели Марковица — ожидаемая доходность ценных бумаг принимается равной средней доходности по данным прошлых периодов. Поэтому модель Марковица рационально использовать при стабильном состоянии фондового рынка, когда желательно сформировать портфель из ценных бумаг различного характера, имеющих более или менее продолжительный срок жизни на фондовом рынке.

Модель Марковица рассматривает в качестве допустимых только стандартные портфели (без коротких позиций).

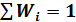Именно это условие накладывает на вектор два ограничения: основное и неотрицательности w_i ³ 0 для всех i.

Ин­вестор по каждому активу находится в длинной (long) позиции.

Модель «Квази – Шарпа» соединяет доходность ценной бумаги с доходностью единичного портфеля и риском этой ценной бумаги с помощью функции линейной регрессии.

Формула доходности ценной бумаги следующая:

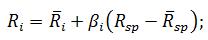
R_i- доходность ценной бумаги;
R_sp- доходность единичного портфеля;
β_i- коэффициент чувствительности к изменению доходности ценной бумаги, коэффициент регрессии в уравнении доходности;
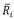–средняя доходность ценной бумаги;
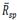– средняя доходность единичного портфеля.

Риск измеряется с помощью коэффициента бета (β), который характеризуется степенью чувствительности к изменению доходности единичного портфеля. Чем выше коэффициент бета, тем сильнее изменяется доходность ценной бумаги от колебания доходности единичного портфеля.

В модели «Квази-Шарпа » риск ценной бумаги представляет собой совокупность коэффициента бета и остаточного риска (σ_ri). Остаточным риском называют степень разброса значений доходности ценной бумаги относительно линии регрессии.
Доходность в модели «Квази – Шарпа» рассчитывается как:

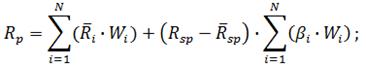
Риск же рассчитывается по следующей формуле:

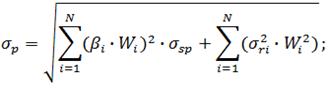
Задача формирования оптимального портфеля по модели «Квази-Шарпа», будет выглядеть следующим образом.

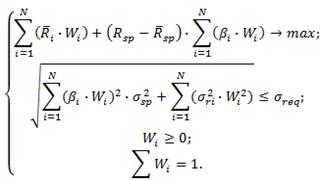
Обратная задача формирования оптимального портфеля, где минимизируется общий риск инвестиционного портфеля с фиксированным уровнем доходности, имеет следующий вид:

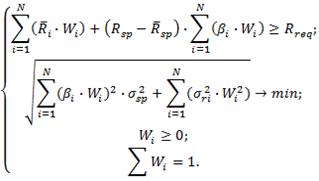
Пример:

Рассмотрим применение модели «Квази – Шарпа» для российского фондового рынка.Данные по котировкам возьмем с сайта finam.ru. За последний год возьмем котировки таких крупных компаний как Газпром (GAZP), Аэрофлот (AFLT), Якутэнерго (YKEN), Сбербанк (SBER), Лукойл (LKOH) и ГМК Норникель (GMKN). Сразу отбросим из рассмотрения акции Газпрома, так как за прошедший год они показали отрицательную прибыль. И занесем все данные в таблицу Excel.

Даны цены акций за год

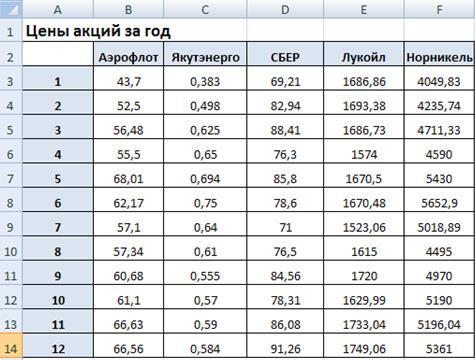
Определим доходность

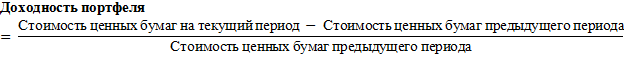
И рассчитаем среднее значение доходности за весь год, то есть за все временные отрезки. Формула для расчета следующая:

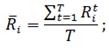
R_it- доходность i-ой акции за период t;
T- рассматриваемое количество временных периодов.

Найдем доходность по каждой акции, среднюю доходность по каждой акции за 12 периодов и доходность единичного портфеля по каждому периоду

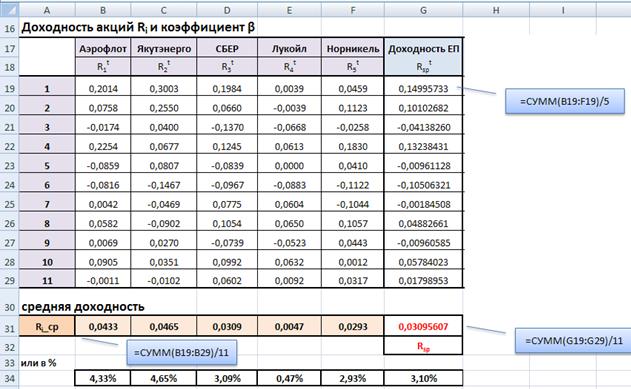
Вычислим коэффициент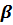

Далее рассчитаем чувствительность изменения доходности акции от изменения доходности единичного портфеля. Чувствительность показывает коэффициент бета (β).

Формула его вычисления следующая:

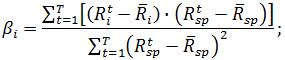
Для упрощения расчета посчитаем сначала знаменатель коэффициента бета, он для всех акций будет одинаков, а после числитель.

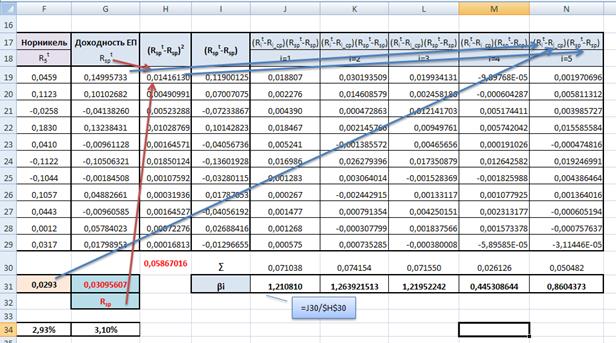
Вычислим остаточные риски

Следующим этапом рассчитаем остаточный риск, который представляет собой степень разброса доходности ценной бумаги относительно линии регрессии. Формула расчета остаточного риска следующая:

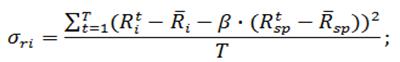
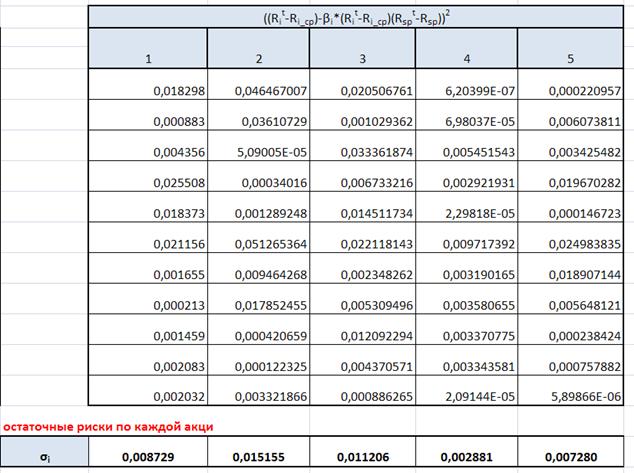
Найдем риск единичного портфеля

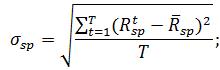
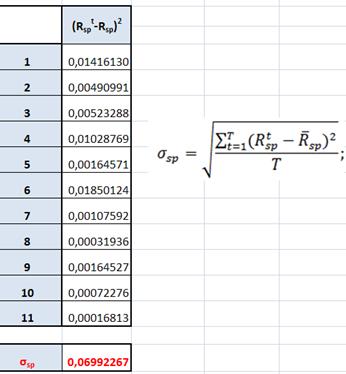
Обобщим данные в таблице

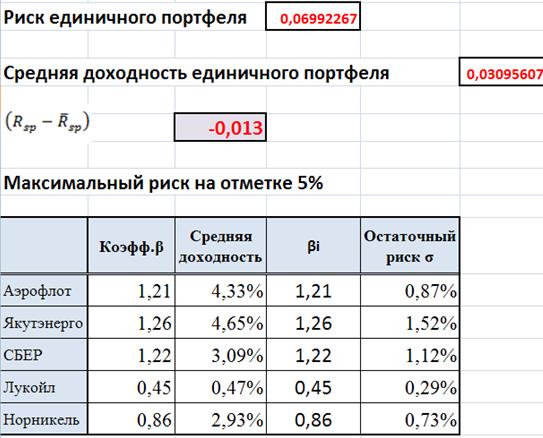
Решим прямую задачу оптимизации, т.е. при условии ограничения на риск 5 %, нужно составить единичный портфель приносящим максимальных доход.

Математическая формулировка

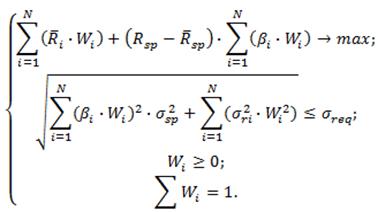
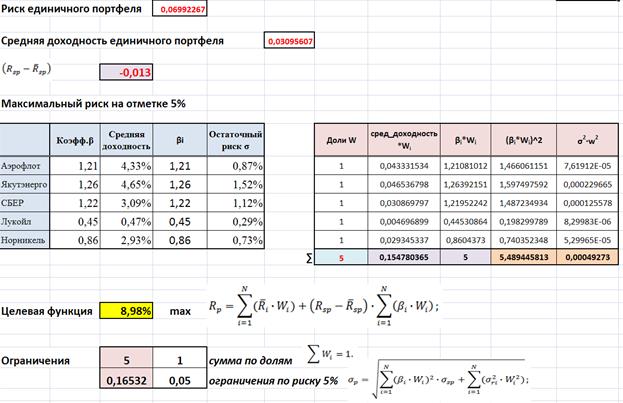
Применим фунцкию Excel «Поиск решения»

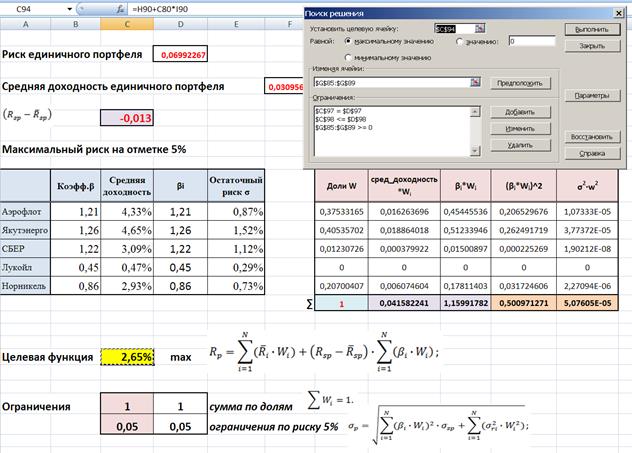
Таким образом, получены следующие результаты:

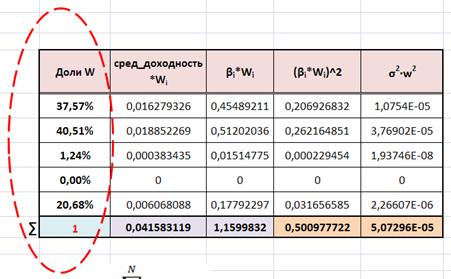
Модель «Квази- Шарпа» рационально использовать при рассмотрении небольшого числа ценных бумаг, принадлежащих одной или нескольким отраслям. С помощью этой модели хорошо поддерживать оптимальную структуру уже созданного инвестиционного портфеля. Недостатком этой модели можно считать не учет глобальных тенденций, которые влияют на доходность портфеля.

Контрольная работа.

Решить обратную задачу (риск стремится к минимуму, доходность не менее 4%)

Модель Шарпа (Sharpe single-index model).

Главным недостатком модели Марковица является то, что она требует очень большого количества информации. Гораздо меньшее количество информации используется в модели У. Шарпа. Последнюю можно считать упрощенной версией модели Марковица.

Согласно Шарпу, прибыль на каждую отдельную акцию строго коррелирует с общим рыночным индексом, что значительно упрощает процедуру нахождения эффективного портфеля.

В основе модели Шарпа лежит метод линейного регрессионного анализа, позволяющий связать две случайные переменные величины - независимую X и зависимую Y линейным выражением типа

Y = a + b·Х.

В модели Шарпа независимой считается величина какого-то рыночного индекса. Сам Шарп в качестве независимой переменной рассматривал доходность, вычисленную на основе индекса Standart and Poor's (S&P500). В качестве зависимой переменной берется доходность какой-то i-ой ценной бумаги.

Взаимосвязь риска с доходностью согласно модели оценки долгосрочных активов описывается следующим образом:

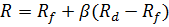
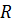– ожидаемая норма доходности

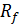– безрисковая ставка доходности, как правило, ставка по государственным облигациям

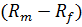- отклонение доходности рынка от безрисковой;

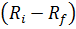– отклонение доходности ценной бумаги от безрисковой;

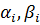- – коэффициенты регрессии

Безрисковый доход измеряется, как правило, по ставкам государственных облигаций, так как те практически без риска. На западе безрисковый доход равен примерно 4-5 %, у нас же - 7-10 %. Доходность рынка в целом - это норма доходности индекса данного рынка. В США, например, индекс S&P 500, а в России - индекс РТС.

Оставшаяся часть формулы представляет собой компенсацию за дополнительный риск, взятый на себя инвестором. Здесь мерой риска является коэффициент 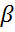, сравнивающий доходность актива с доходностью рынка.

Коэффициент 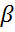определяется по формуле:

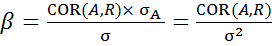
где 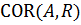- корреляция между доходностью ценной бумаги A и средним уровнем доходности ценных бумаг на рынке;

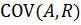- ковариация между доходностью ценной бумаги A и средним уровнем доходности ценных бумаг на рынке;

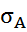- стандартное отклонение доходности по конкретной ценной бумаге;

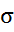- стандартное отклонение доходности по рынку ценных бумаг в целом.

Уровень риска отдельных ценных бумаг определяется на основании таких значений:

β = 1 - средний уровень риска;

β > 1 - высокий уровень риска;

β < 1 - низкий уровень риска.

Акции с большой бетой (β > 1) называют агрессивными, с низкой бетой (β < 1) - защитными. Например, агрессивными являются акции компаний, чьи доходы существенно зависят от конъюнктуры рынка. Когда экономика на подъеме, агрессивные акции приносят большие прибыли. Например, акции автомобилестроительных компаний являются агрессивными. Инвесторы, ожидающие подъема экономики, покупают агрессивные акции, обеспечивающие больший уровень доходности в условиях растущего рынка, чем защитные. Акции компаний, чья прибыль в меньшей степени зависит от состояния рынка, являются защитными (например, акции компаний коммунальной сферы). Доходы таких компаний сокращаются в меньшей степени в условиях экономического спада. Поэтому использование защитных акций в периоды кризисов позволяет инвестору извлечь большую прибыль в сравнении с агрессивными акциями.

Если b-коэффициент акции равен единице, то доходность акции изменяется в точном соответствии со всем рыночным портфелем, ¾ это акция среднего риска. Если b = 2, то степень риска акции вдвое выше, чем степень риска рыночного портфеля. При b = 0,5 акция имеет только половину риска средней акции.

По портфелю ценных бумаг β рассчитывается как средневзвешенный β - коэффициент отдельных видов входящих в портфель инвестиций, где в качестве веса берется их удельный вес в портфеле.

b_p = b₁ ´ w₁ + b₂´ w₂ +…+ b_n ´ w_n

или

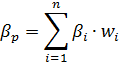
Где 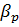¾ бета портфеля, который отражает подвижность портфеля относительно всего рынка; 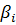¾ бета i-й акции; 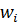¾ доля инвестиций в i-ю акцию.

Пример:

Например, инвестор имеет 40 тыс. долл. и сформировал портфель из четырех акций, вложив в каждый вид акций по 10 тыс. долл. Если каждая акция имеет b = 0,8, то бета такого портфеля также будет равен 0,8:

b_p = 0,8 ´ 0,25 + 0,8 ´ 0,25 + 0,8 ´ 0,25 = 0,8.

Такой портфель будет менее рисковым, чем весь рынок акций, и будет испытывать меньшее колебание доходности и стоимости портфеля по сравнению со всем рынком.

Теперь представим, что одна из акций продана и заменена акцией, имеющей b = 2, тогда риск портфеля увеличится и его бета возрастет:

b_p = 0,8 ´ 0,25 + 0,8 ´ 0,25 + 0,8 ´ 0,25 + 2,0 ´ 0,25 = 1,1.

Если одну из акций заменить на акцию b = 0,2, то бета портфеля снизится и составит:

b_p = 0,8 ´ 0,25 + 0,8 ´ 0,25 + 0,8 ´ 0,25 + 0,2 ´ 0,25 = 0,65.

Таким образом, риск портфеля может быть снижен путем включения в портфель акций, имеющих низкое значение b-коэффициента.

Оптимизация состава портфеля ценных бумаг Шарпа

Математическая модель портфеля ценных бумаг Шарпа имеет вид

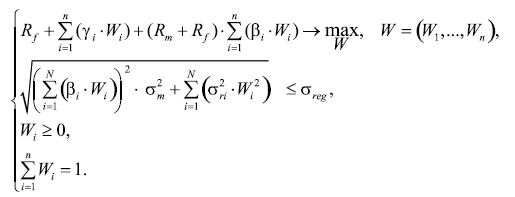
где

γi, βi, Wi, σri – соответственно избыточная доходность, вес, риск, остаточный риск, Rf – доходность ценных бумаг; Rm – ожидаемая доходность рынка в целом; σm – среднее квадратическое отклонение доходности рынка; σreg – максимально допустимая величина риска портфеля ценных бумаг.

В модели предполагается, что величина σreg заранее задана (например, экспертом). Перейдем от модели к модели, в которой дополнительно минимизируется величина риска портфеля:

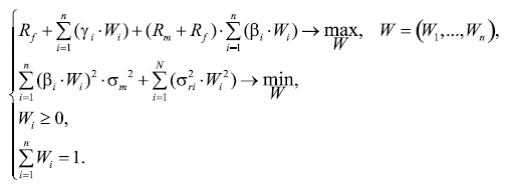
Модель называют моделью оптимизации портфеля Шарпа.

От данной модели с двумя критериями, путем линейной свертки критериев перейдем к модели с одним критерием:

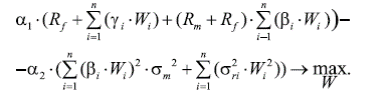
и теми же ограничениями

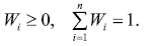
Модель демонстрирует прямую связь между риском ценной бумаги и ее доходностью, что позволяет ей показать справедливую доходность относительно имеющегося риска и наоборот.

Уравнение, записанное без случайной погрешности, является уравнением линейной регрессии. Параметр «бета» поэтому является коэффициентом регрессии и может быть определен по формул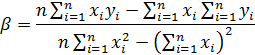е: Где: 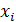– доходность рынка в i-й период времени; 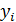– доходность ценной бумаги в i-й период времени; 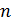– количество периодов.По Шарпу показатель «альфа» (его также называют сдвигом) определяет составляющую доходности бумаги, которая не зависит от движения рынка 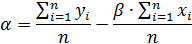В соответствие с одной из точек зрения, «альфа» является своего рода мерой недо- или переоценки рынком данной бумаги. Положительная «альфа» свидетельствует о переоценке рынком данной бумаги. Отрицательная «альфа» свидетельствует о недооценке рынком данной бумаги. Случайная погрешность e показывает, что индексная модель Шарпа не очень точно объясняет доходности ценной бумаги. Разность между действительным и ожидаемым значениями при известной доходности рыночного индекса приписывается случайной погрешности. Случайную погрешность можно рассматривать как случайную переменную, которая имеет распределение вероятностей с нулевым математическим ожиданием и стандартным отклонением, вычисляемым по формуле: 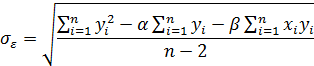Истинное значение коэффициента «бета» ценной бумаги невозможно установить, можно лишь оценить это значение. Так что даже если бы истинное значение «беты» оставалось постоянным всегда, его оценка, полученная по методу наименьших квадратов, все равно бы менялась бы во времени из-за ошибок при оценке – ошибок выборки. Стандартная ошибка «беты» есть попытка оценить величину таких ошибок: 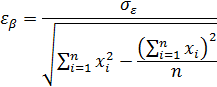Аналогично стандартная ошибка для «альфы» дает оценку величины отклонения прогнозируемого значения от «истинного»: 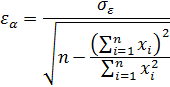Для характеристики конкретной ценной бумаги используются и другие параметры. R-squared (R²), или коэффициент детерминации, равен квадрату коэффициента корреляции цены бумаги и рынка. R-squared меняется от нуля до единицы и определяет степень согласованности движения рынка и бумаги. 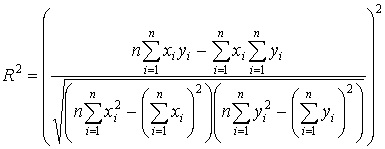Коэффициент детерминации представляет собой пропорцию, в которой изменение доходности ценной бумаги связано с изменением доходности рыночного индекса. Другими словами, он показывает, в какой степени колебания доходности ценной бумаги можно отнести за счет колебаний доходности рыночного индекса. Если этот коэффициент равен единице, то бумага полностью коррелирует с рынком, если равен нулю, то движение рынка и бумаги абсолютно независимы. Ошибки показателей «бета» и «альфа» определяются непосредственно ошибкой регрессионной модели. Естественно, в первую очередь они зависят от глубины расчета. При различных стадиях рынка (растущий, падающий) для достижения лучшего эффекта можно пользоваться следующими комбинациями коэффициентов:

	На покупку	На продажу
Падающий рынок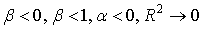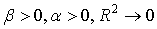
Растущий рынок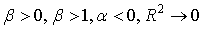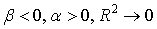

На западных рынках значения a, b, R² регулярно рассчитываются

для всех ценных бумаг и публикуются вместе с индексами. Пользуясь этой

информацией, инвестор может сформировать собственный портфель ценных бумаг. На российском рынке профессионалы постепенно тоже начинают использовать a-, b-, R²-анализ.