Тема 1. Потоки платежей
Проведение практически любой финансовой операции порождает движение денежных средств. Такое движение может характеризоваться возникновением отдельных платежей, или множеством выплат и поступлений, распределенных во времени.
В финансовой практике зачастую контракты предусматривают не отдельные разовые платежи, а серию платежей, распределенных во времени (регулярные выплаты). Например, погашение долгосрочного кредита, вместе с начисленными на него процентами; периодические взносы на расчетный счет, на котором формируется некоторый фонд различного назначения (инвестиционный, пенсионный, страховой, резервный, накопительный и т.д.); дивиденды, выплачиваемые по ценным бумагам; выплаты пенсий из пенсионного фонда и пр.
Поток платежей (cash flow –  ) представляет собой ряд последовательных во времени выплат и поступлений
) представляет собой ряд последовательных во времени выплат и поступлений  ,
,  , …,
, …,  .
.
Потоки платежей являются неотъемлемой частью всевозможных финансовых операций: с ценными бумагами, в управлении финансами предприятий, при осуществлении инвестиционных проектов, в кредитных операциях, при оценке бизнеса, при оценке недвижимости, выборе альтернативных вариантов финансовых операций и т.п.
Члены потока могут быть как положительными величинами (поступления), так и отрицательными величинами (выплатами), а временные интервалы между членами такого потока могут быть равными и неравными.
Поток платежей, все члены которого имеют одинаковое направление (знак), а временные интервалы между последовательными платежами постоянны, называется финансовой рентой или аннуитетом.
При рассмотрении финансовой ренты используются основные категории:
- член ренты (  ) – величина каждого отдельного платежа;
) – величина каждого отдельного платежа;
- период ренты (  ) – временной интервал между членами ренты;
) – временной интервал между членами ренты;
- срок ренты (  ) – время от начала финансовой ренты до конца последнего ее периода;
) – время от начала финансовой ренты до конца последнего ее периода;
- процентная ставка ( 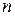 ) – ставка, используемая при наращении платежей, из которых состоит рента;
) – ставка, используемая при наращении платежей, из которых состоит рента;
- наращенная сумма (  ) – сумма долга на какой-либо момент в будущем;
) – сумма долга на какой-либо момент в будущем;
- современная стоимость (  ) – современная величина потока платежей.
) – современная величина потока платежей.
При определении члена ренты возможны два варианта, зависящие от того, какая величина является исходной:
а) наращенная сумма. Если сумма долга определена на какой-либо момент в будущем, тогда величину последующих взносов в течение k лет при начислении на них процентов по ставке n можно определить по формуле:
 , (1)
, (1)
б) известна современная величина финансовой ренты, тогда, исходя из ставки процента и срока ренты, разовый платеж находится по формуле:
 . (2)
. (2)
Как известно, погашение займа осуществляется за счет платежей, состоящих из части основного долга (суммы кредита) и процентов. Но рассчитываться размер этих платежей может по-разному.
В финансовой практике наиболее часто встречаются так называемые простые или обыкновенные аннуитеты (ordinary annuity, regular annuity), которые предполагают получение или выплаты одинаковых по величине сумм на протяжении всего срока операции в конце каждого периода (года, полугодия, квартала, месяца и т.д.).
Простой аннуитет обладает двумя важными свойствами:
- все его элементы равны между собой;
- отрезки между выплатой/поступлением сумм  одинаковы.
одинаковы.
Если рассматривать кредитные отношения, то за аннуитетный платеж будем считать равный по сумме ежемесячный платеж по кредиту, который включает в себя сумму начисленных процентов за кредит и сумму основного долга.
Расчёт аннуитетного платежа можно производить по формуле (2), в этом случае вводится обозначение:
 – размер ежемесячного аннуитетного платежа по кредиту;
– размер ежемесячного аннуитетного платежа по кредиту;
 – сумма кредита;
– сумма кредита;
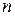 – процентная ставка в долях за период (месяц);
– процентная ставка в долях за период (месяц);
 – количество месяцев, на которые берётся кредит.
– количество месяцев, на которые берётся кредит.
Другим не менее распространенным способом погашения ссуды сегодня являются дифференцированные платежи, размер которых каждый месяц будет разным и постепенно уменьшающимся. Основной долг при этом делится на количество месяцев действия кредита и уплачивается равными долями. Проценты начисляются на остаток задолженности, за счет чего их сумма всегда уменьшается.
Таким образом, основное отличие между аннуитетом и дифференцированными взносами заключается в том, изменяется ли сумма ежемесячного платежа по кредиту или остается постоянной на протяжении всего срока займа.
В случае дифференцированных платежей величина погашения долга определяется следующим образом:
 , (3)
, (3)
где  – величина погашения основной суммы долга;
– величина погашения основной суммы долга;
 – первоначальная сумма кредита;
– первоначальная сумма кредита;
 – количество периодов (месяцев), на которые берётся кредит;
– количество периодов (месяцев), на которые берётся кредит;
Проценты начисляются на уменьшаемую сумму основного долга:
 , (4)
, (4)
где  – величина погашения процентов по кредиту за
– величина погашения процентов по кредиту за 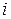 -ый месяц;
-ый месяц;
 – остаток ссудной задолженности (суммы обязательства) на начало
– остаток ссудной задолженности (суммы обязательства) на начало 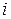 -го месяца;
-го месяца;
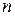 – процентная ставка в долях за период (месяц), равная 1/12 от годовой процентной ставки, установленной на сумму кредита;
– процентная ставка в долях за период (месяц), равная 1/12 от годовой процентной ставки, установленной на сумму кредита;
 .
.
Тогда величина дифференцированного платежа по кредиту по каждому месяцу определяется как сумма уплачиваемых процентов и сумма погашения основного долга:
 , (5)
, (5)
где  – размер дифференцированного платежа по кредиту за
– размер дифференцированного платежа по кредиту за 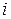 -ый месяц,
-ый месяц,  .
.
В финансовых операциях возможны ситуации, когда выплаты по кредиту производятся в сумме, большей установленного аннуитета. В таких случаях говорят о частичном досрочном погашении кредита. При этом кредитный договор с банком позволяет уменьшить либо размер ежемесячного аннуитетного платежа, либо срок кредитования.
Рассмотрим оба варианта развития событий в случае частичного досрочного погашения кредита.
1. Уменьшение размера ежемесячного аннуитетного платежа (без изменения срока кредитования).
Для определения новой суммы аннуитета достаточно подставить в формулу аннуитета новое значение суммы кредита (остаток после погашения) и срок, оставшийся до погашения кредита.
2. Уменьшение срока кредитования (без изменения размера ежемесячного аннуитетного платежа).
Новый срок кредитования (с момента частичного досрочного погашения кредита) можно определить по формуле:
 , (6)
, (6)
где  – новый срок кредитования (с момента частичного досрочного погашения кредита);
– новый срок кредитования (с момента частичного досрочного погашения кредита);
 – остаток ссудной задолженности (суммы кредита) после частичного досрочного погашения в
– остаток ссудной задолженности (суммы кредита) после частичного досрочного погашения в  -ый месяц;
-ый месяц;
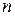 – процентная ставка в долях за период (месяц), равная 1/12 от годовой процентной ставки, установленной на сумму кредита;
– процентная ставка в долях за период (месяц), равная 1/12 от годовой процентной ставки, установленной на сумму кредита;
 – размер ежемесячного аннуитетного платежа по кредиту.
– размер ежемесячного аннуитетного платежа по кредиту.
Замечание. Значение  всегда округляется в сторону увеличения, т.е. если
всегда округляется в сторону увеличения, т.е. если  , то принимаем
, то принимаем  .
.
Задание
На приобретение квартиры взят кредит на 3 года в размере 500 тыс. руб. под 12% годовых. Проценты по кредиту начисляются ежемесячно на остаток долга.
Необходимо:
1. Определить размер ежемесячного аннуитетного платежа по кредиту.
2. Составить в Microsoft Excel график аннуитетных платежей.
3. Определить общую сумму начисленных процентов.
4. Составить в Microsoft Excel график погашения кредита при условии, что основная сумма долга погашается равными частями, и сравнить суммы начисленных процентов при дифференцированных и аннуитетных платежах.
5. Составить в Microsoft Excel график аннуитетных платежей при условии частичного досрочного погашения кредита (без каких-либо ограничений по сумме и штрафов), если 26-ой платеж составляет 50 тыс.руб., а кредитный договор с банком позволяет уменьшить:
а) размер ежемесячного платежа;
б) срок кредитования.
6. Ответить на вопрос: «Как изменится общая сумма выплат в случае частичного досрочного погашения кредита?»
Решение.
1. Размер ежемесячного аннуитетного платежа по кредиту определим двумя способами.
1 способ. Используя формулу (2) для расчета ежемесячного аннуитетного платежа, получим
 руб.
руб.
Таким образом, ежемесячно необходимо будет возвращать сумму 16 607,15 руб.
2 способ. Выполним расчеты с использованием Microsoft Excel.
Создадим новую книгу в Microsoft Excel и назовем ее «Потоки платежей». Введем в ячейки A1:B4 листа 1 книги «Потоки платежей» исходные данные, как на рис. 1.

Рис. 1. Ввод исходных данных задачи 1
Далее для вычисления размера ежемесячного аннуитетного платежа по кредиту выполним следующие действия:
а) в ячейку А6 ввести текст «CF»;
б) выделить ячейку В6 и выполнить команду «Вставка»/«Функция», в открывшемся окне Мастера функции выбрать категорию «Финансовые», функцию ПЛТ(). Данная функция возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянства процентной ставки;
в) заполнить поля функции ПЛТ согласно рис. 2: в поле «Ставка» указывается процентная ставка в долях за месяц, равная 1/12 от годовой процентной ставки, установленной в ячейкеВ4, в поле «Кпер» – общее количество месяцев выплат по кредиту, равное произведению, в поле «Пс» – сумма кредита.

Рис. 2. Окно аргументов функции ПЛТ
Результат расчета величины отдельного аннуитетного платежа с использованием встроенной функции ПЛТ в Microsoft Excel представлен на рис. 3.

Рис. 3. Результат вычисления по функции ПЛТ
Полученное значение отрицательно, поскольку оно представляет собой величину ежемесячного платежа по кредиту. Абсолютное значение аннуитета, рассчитанного с помощью функции ПЛТ в Microsoft Excel, совпадает со значением, найденным по формуле (2).
2. В финансовых операциях зачастую требуется вычисление обобщающих характеристик по каждому платежу и последующему их суммированию.
В этом случае для расчета аннуитетного платежа по кредиту по каждому месяцу удобно использовать формулу (2),
где  – размер аннуитетного платежа по кредиту за
– размер аннуитетного платежа по кредиту за 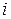 -ый месяц;
-ый месяц;
 – остаток ссудной задолженности (суммы обязательства) на начало
– остаток ссудной задолженности (суммы обязательства) на начало 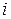 -го месяца;
-го месяца;
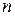 – процентная ставка в долях за период (месяц), равная 1/12 от годовой процентной ставки, установленной на сумму кредита;
– процентная ставка в долях за период (месяц), равная 1/12 от годовой процентной ставки, установленной на сумму кредита;
 – количество процентных периодов (месяцев), оставшихся до окончательного погашения ссудной задолженности (суммы обязательства).
– количество процентных периодов (месяцев), оставшихся до окончательного погашения ссудной задолженности (суммы обязательства).
С помощью Microsoft Excel составим график аннуитетных платежей (т.е. график погашения кредита) для рассматриваемой задачи.
Для этого на листе 1 книги «Потоки платежей» Microsoft Excel создадим таблицу как на рис. 4.
В ячейку С11 таблицы введем формулу (2) для определения размера аннуитетного платежа, в ячейку Е11 – формулу для определения размера платежа в погашение процентов, как произведение остатка по кредиту к моменту 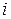 -го платежа на процентную ставку в долях за месяц, в ячейку D11 – формулу для определения размера платежа в погашение долга, как разницу между величиной аннуитета и размером платежа в погашение процентов по кредиту (рис. 4). В ячейку F11 вводим формулу для определения остатка задолженности по кредиту после платежа, как разницу между остатком по кредиту к моменту
-го платежа на процентную ставку в долях за месяц, в ячейку D11 – формулу для определения размера платежа в погашение долга, как разницу между величиной аннуитета и размером платежа в погашение процентов по кредиту (рис. 4). В ячейку F11 вводим формулу для определения остатка задолженности по кредиту после платежа, как разницу между остатком по кредиту к моменту  -го платежа и размером
-го платежа и размером  -го платежа в погашение долга (рис. 4).
-го платежа в погашение долга (рис. 4).

Рис 4. Ввод формул в таблицу погашения кредита по аннуитетной схеме
Далее скопируем формулы в ячейках С11:F11 до конца таблицы и добавим итоговую строку (рис. 5).

Рис. 5. Составление графика аннуитетных платежей по кредиту
В результате получим следующий график аннуитетных платежей по кредиту:

Рис. 6. График аннуитетных платежей по кредиту (результат вычислений)
В этой таблице можно увидеть все текущие параметры кредита – размер аннуитетного платежа, его части, идущие в погашение долга и процентов, а также остаток задолженности по кредиту после каждого платежа.
Из таблицы видно, что ежемесячная сумма платежа по процентам из месяца в месяц уменьшается, а ежемесячная сумма платежа по основному долгу – увеличивается.
В случае аннуитетной схемы погашения кредита за 3 года банку будет выплачено всего 597 857,58 руб. (итоговое значение по столбцу «Аннуитетный платеж» на рис. 6).
3. Общую сумму начисленных процентов можем увидеть в итоговой строке по соответствующему столбцу построенного графика аннуитетных платежей (рис. 6).
Итак, за 3 года банку будет выплачено процентов на сумму 97 857,58 руб.
4. Составим в Microsoft Excel график погашения кредита при условии, что основная сумма долга погашается равными частями (дифференцированные платежи).
Для этого на листе 2 книги «Потоки платежей» Microsoft Excel введем в ячейки A1:B4 исходные данные, как на рис. 1.
Далее создадим таблицу согласно рис. 7.
В ячейку D9 таблицы введем формулу (3) для определения размера платежа в погашение долга, в ячейку Е9 – формулу для определения размера платежа в погашение процентов, как произведение остатка по кредиту к моменту 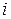 -го платежа на процентную ставку в долях за месяц, в ячейку C9 – формулу для определения размера дифференцированного платежа по кредиту, как сумму соответствующих платежей в погашение процентов и в погашение долга (рис. 7). В ячейку F9 вводим формулу для определения остатка задолженности по кредиту после платежа, как разницу между остатком по кредиту к моменту
-го платежа на процентную ставку в долях за месяц, в ячейку C9 – формулу для определения размера дифференцированного платежа по кредиту, как сумму соответствующих платежей в погашение процентов и в погашение долга (рис. 7). В ячейку F9 вводим формулу для определения остатка задолженности по кредиту после платежа, как разницу между остатком по кредиту к моменту  -го платежа и размером
-го платежа и размером  -го платежа в погашение долга (рис. 7).
-го платежа в погашение долга (рис. 7).

Рис. 7. Ввод формул в таблицу погашения кредита по дифференцированной схеме
Далее скопируем формулы в ячейках С9:F9 до конца таблицы и добавим итоговую строку (рис. 8).

Рис. 8. Составление графика дифференцированных платежей по кредиту
В результате получим следующий график дифференцированных платежей по кредиту:

Рис. 9. График дифференцированных платежей по кредиту
(результат вычислений)
В этой таблице можно увидеть все текущие параметры кредита – размер дифференцированного платежа по каждому месяцу, его части, идущие в погашение долга и процентов, а также остаток задолженности по кредиту после каждого платежа. Из таблицы видно, что ежемесячная сумма платежа, также как и ежемесячная сумма платежа по процентам, из месяца в месяц уменьшается. Общую сумму начисленных процентов и общую сумму выплат можем увидеть в итоговой строке по соответствующим столбцам построенного графика дифференцированных платежей (рис. 9).
Итак, в случае дифференцированной схемы погашения кредита за 3 года банку будет выплачено всего 592 500,00 руб., из которых процентов – на сумму 92 500,00 руб.
Если сравнить графики платежей по аннуитетной (рис. 6) и дифференцированной (рис. 9) схемам, видим, что размер аннуитетных платежей будет меньше в начале срока погашения, примерно в середине графика они сравняются, но затем сумма дифференцированных начнет уменьшаться, а сумма аннуитетных так и останется неизменной.
Сравнивая суммы начисленных процентов по рассматриваемым схемам, приходим к выводу, что меньшая сумма процентов по кредиту выплачена по дифференцированной схеме, эта разница составляет 5 357,58 руб.
5. Рассмотрим случай частичного досрочного погашения кредита, когда 26-ой платеж составляет 50 000 руб., если кредитный договор с банком позволяет уменьшить размер ежемесячного аннуитетного платежа (без изменения срока кредитования).
Для определения новой суммы аннуитета необходимо на листе 1 книги «Потоки платежей» Microsoft Excel в ячейку С36, соответствующую 26-ому платежу по кредиту, внести значение 50 000. В результате по формулам пересчитывается сумма аннуитета, которую необходимо будет выплачивать в последующие месяцы (рис. 10).

Рис. 10. Пересчет аннуитета в случае частичного досрочного погашения кредита (при условии уменьшения аннуитета)
В результате получен новый график при частичном досрочном погашении кредита (в случае, когда кредитный договор с банком позволяет уменьшить размера аннуитетного платежа). По новому графику за 3 года банку будет выплачено 595 993,56 руб., из которых процентов – на сумму 95 993,56 руб. (рис. 10).
Теперь рассмотрим случай, когда при частичном досрочном погашении кредитный договор с банком позволяет уменьшить срок кредитования (без изменения размера ежемесячного аннуитетного платежа).
Для этого на листе 3 книги «Потоки платежей» Microsoft Excel введем в ячейки A1:B4 исходные данные, как на рис. 1.
Далее создадим таблицу согласно рис. 11.
В ячейку С11 таблицы введем формулу для определения размера аннуитетного платежа с помощью встроенной функции ПЛТ в Microsoft Excel, в ячейку Е11 – формулу для определения размера платежа в погашение процентов, как произведение остатка по кредиту к моменту 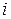 -го платежа на процентную ставку в долях за месяц, в ячейку D11 – формулу для определения размера платежа в погашение долга, как разницу между величиной аннуитета и размером платежа в погашение процентов по кредиту (рис. 11). В ячейку F11 вводим формулу для определения остатка задолженности по кредиту после платежа, как разницу между остатком по кредиту к моменту
-го платежа на процентную ставку в долях за месяц, в ячейку D11 – формулу для определения размера платежа в погашение долга, как разницу между величиной аннуитета и размером платежа в погашение процентов по кредиту (рис. 11). В ячейку F11 вводим формулу для определения остатка задолженности по кредиту после платежа, как разницу между остатком по кредиту к моменту  -го платежа и размером
-го платежа и размером  -го платежа в погашение долга (рис. 11).
-го платежа в погашение долга (рис. 11).

Рис. 11. Ввод формул в таблицу погашения кредита по аннуитетной схеме в случае частичного досрочного погашения кредита
(при условии уменьшения аннуитета)
Далее скопируем формулы в ячейках С9:F9 до конца таблицы и добавим итоговую строку (рис. 12).

Рис. 12. Составление графика аннуитетных платежей по кредиту в случае частичного досрочного погашения (при условии уменьшения аннуитета)
В результате получим следующий график аннуитетных платежей по кредиту:

Рис. 13. График аннуитетных платежей по кредиту
(результат вычислений)
На рис. 13 получили тот же график аннуитетных платежей, что и на рис. 6. Далее на листе 3 в ячейку С34, соответствующую 26-ому платежу по кредиту, вносим значение 50 000, тогда в ячейке F34 пересчитается остаток по кредиту после частичного досрочного погашения в 26-ой месяц. Он составляет 123 898,58 руб. (рис. 14).

Рис. 14. Пересчет остатка по кредиту после частичного досрочного погашения (при условии уменьшения аннуитета)
Тогда новый срок кредитования (с момента частичного досрочного погашения кредита) определим по формуле (6):
 .
.
Это означает, что последним платежом по кредиту будет 34-ый платеж (поскольку 26+8=34). Тогда содержимое ячеек С43:F44 мы удаляем, в связи с сокращением срока платежа по кредиту. Ячейка D42 (столбец «В погашение долга»), соответствующая 34-му платежу, будет равна остатку по кредиту на начало текущего месяца, для этого изменим формулу в этой ячейке на следующую: «=F41». Ячейка же С42 будет соответствовать сумме платежей в погашение долга и процентов, для этого изменим формулу в этой ячейке на следующую: «=D42+E42».
В результате пересчитывается остаток по кредиту после 34-го платежа, который составит нулевое значение рис. 15.

Рис. 15. Новый график аннуитетных платежей после частичного досрочного погашения кредита (при условии уменьшения срока кредитования)
В результате получен новый график при частичном досрочном погашении кредита (в случае, когда кредитный договор с банком позволяет уменьшить срок кредитования). По этому графику за 3 года банку будет выплачено 594 599,10 руб., из которых процентов – на сумму 94 599,10 руб. (рис. 15).
6. Общую сумму выплат можем увидеть в итоговых строках по соответствующему столбцу построенных графиков анниутетных платежей (рис. 6, рис. 10 и рис. 15).
Итак, в случае аннуитетной схемы погашения кредита за 3 года банку (без досрочного погашения) будет выплачено всего 597 857,58 руб. (рис. 6).
В случае частичного досрочного погашения кредита при условии уменьшения аннуитетного платежа общая сумма выплат составит 595 993,56 руб. (рис. 10), что в свою очередь меньше общей суммы выплат по графику на 1 864,02 руб.
В случае же частичного досрочного погашения кредита при условии уменьшения срока кредитования общая сумма выплат составит 594 599,10 руб. (рис. 15), что в свою очередь меньше общей суммы выплат по графику на 3 258,48 руб., и меньше общей суммы выплат в случае частичного досрочного погашения кредита при условии уменьшения аннуитетного платежа на 1 394,46 руб.
