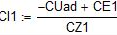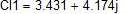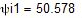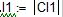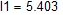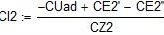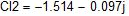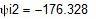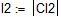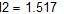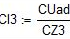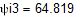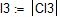I. Электрические цепи постоянного тока

Задание 1

1. Упростить схему, заменив последовательно и параллельно соединенные резисторы четвертой и шестой ветвей эквивалентными. Дальнейший расчет вести для упрощенной схемы.

2. Определить токи во всех ветвях схемы методом контурных токов.

3. Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.

4. Определить токи во всех ветвях схемы методом узловых потенциалов.

5. Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить между собой.

6. Составить баланс мощностей в исходной схеме (схеме с источником тока) вычислив суммарную мощность нагрузок (сопротивлений).

7. Определить ток I₁ в заданной по условию схеме с источником тока, используя метод эквивалентного генератора.

8. Начертить потенциальную диаграмму для любого замкнутого контура включающего обе ЭДС_.

Исходные данные таблица 1.1

R1	R2	R3	R’4	R”4	R5	R’6	R”6	E2	E3	J2	J3
Ом	В	А
	12,5			37,5	17,5

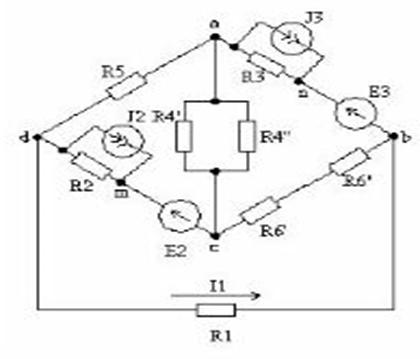
Рис. 1.1 Электрическая схема цепи

1. Упростить схему, заменив последовательно и параллельно соединенные резисторы четвертой и шестой ветвей эквивалентными. Дальнейший расчет вести для упрощенной схемы

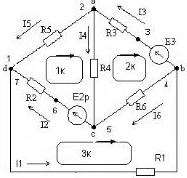
Рис. 1.2 Упрощенная схема электрической цепи

R₆ = R'₆ + R"₆ = 14+6=20 (Ом);

R₄ = (R'₄ * R''₄) / (R'₄ + R''₄) = (525*37,5) / (525+37,5) = 35 (Ом);

E_Т2 = R₂J₂ = 12,5*2 =25 (В).

Эквивалентная схема рисунка 1.2 Таблица 1.2

R1	R2	R3	R4	R5	R6	E2	E3	EТ2
Ом	В
	12,5			17,5

2. Определить токи во всех ветвях схемы методом контурных токов.

На основании законов Кирхгофа запишем систему уравнений для контурных токов I11, I22, I33:

I11: R2I2 – R5I5 – R4I4= E2 - Е2

I22: R6I6 - R4I4 – R3I3 = -Е3

I33: -R2I2 – R6I6 – R1I1 = E2 - Е2

Рассчитаем коэффициенты данной системы:

I11: (12,5+17,5+35)I11 – 12,5I22 - 20I3 = 0

I22: (20+35+20)I22 + 35I11 - 20I33 = -55

I33: (15+12,5+20)I33+-20I22 + 12,5I11 = 0

Подставим полученные коэффициенты в исходную систему:

I11: 65I11 – 35I22 -12,5I33 = 0

I22: -35I11 + 75I22 -20I33 = -55

I33: 12,5I11 -20I22 + 47,5I33 = 0

Решаем полученную систему методом Крамера; вычисляем определители системы и выражаем искомые токи через контурные токи:

I11=I5=-0,9

I22=I3=-1,4

I33=I1=-0,8

I4=I11-I22=0,5

I2=I11-I33=-0,1

I6=I22-I33=-0,6

3. Баланс мощностей

∑Рист=∑Рнагрузок

∑Рист=I2E2-I2E’2+I3E3=77(Вт)

∑Pнагрузок= R₁I₁²+ R₂I₂²+ R₃I₃²+ R₄I₄²+ R₅I₅²+ R₆I₆² = 79,5(Вт)

5. Метод узловых потенциалов.

Система для расчета потенциалов в узлах:

Уз 1: (g3+g5+g4)φa – g3φb – g4φc = E3g3;

Уз 2: -g3φa + g1(g6+g3+g1)φb – g6фc = -E3g3;

Уз 4: -g4φa – g6φb + фd(g4+g6+g2)= 0

Найдем проводимости ветвей:

g1=1/R1=1/13.5=0.07407 (Oм-1);

g2=1/R2=1/30=0.0333 (Oм-1);

g3=1/R3=1/24=0.04167 (Oм-1);

g4=1/R4=1/60=0.01667 (Oм-1);

g5=1/R5=1/45=0.0222 (Oм-1);

g6=1/R6=1/33=0.03 (Oм-1).

Уз 1: 0,14φa – 0,05φb – 0,03φc = 2,75

Уз 2: -0,05φa + 0,16φb – 0,05φc = -2,75

Уз 3: -0,03φa – 0,05φb + 0,16φc = 0

ⱷ_a =14,7

ⱷ_b=-12,9

ⱷ_c=-1,29

Находим истинные токи:

I₁ = (φ_d – φ_b ) / R₁ = 0,8 (A);

I₂ = (0+φ_c - φ_d)/R₂ = -0,1 (A);

I₃ = (E₃ +φ_b - φ_a)/R₃ = -1,37 (А);

I₄ = (φ_a – φ_c)/R₄= 0,456 (A);

I_5­ = (φ_a – φ_d)/R₅ = -0,84(A);

I₆ = (φ_b – φ_c)/R6 = -0,58 (A).

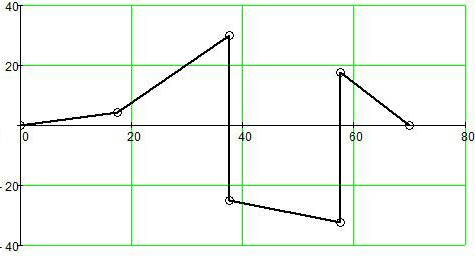
Ф_d=0,ф_a=ф_d+I5R5,ф_n=ф_а+I3R3,ф_b=ф_n-E3,ф_c=ф_b-I6R6,ф=0

6. Метод эквивалентного генератора.

I1=E_эг/(R1+R_эг)

U_dbxx+I3R3-I2R5+E3=0

I11_xx(R5+R4+R2)- I22R4=0

I22_хх(R4+R3+R6)-I11R4=-E3

I11=I2 I2=(ф_с-ф_а)/(R2+R5) I2=0,6

I22=I3 I3=ф_с-ф_а+Е3/(R6+R3) I3=0,8

R_эг=R_d+(R_c*R₆)(R_a+R3)/R_c+R₆+R_a+R₃=63

R_d=R_5*R₂/(R₅+R₂+R₄)=3

R_a=R_5*R₄/( R₅+R₂+R₄)=9

R_c= R_2*R₄/( R₅+R₂+R₄)=6

I_эг=Е_эг/(R1+R_эг)=0,78

Расчет цепи переменного синусоидального тока.

Задание 2

1.На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав ее в двух формах: а)дифференциальной; б)символической;

2.Определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчета линейных электрических цепей.

3.По результатам, полученным в пункте №2, определить показание ваттметра.

4.Построить топографическую диаграмму, совмещенную с векторной диаграммой токов, потенциал а, указанной на схеме принять равным нулю.

Исходные данные варианта 4. Таблица 2.1

L1	L3	C1	C3	R2		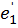		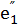	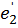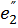f
мГн	мкФ	Ом	B	Гц
20,1		17,7	26,5		70,5cos (ωt-103)		84,6sin(ωt-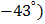

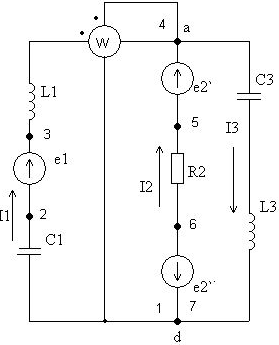
Рисунок 2.1 Электрическая схема цепи синусоидального тока

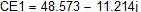
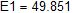
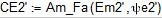
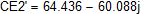
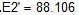
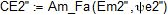
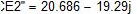
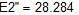
Производим расчет угловой частоты.

ω = 2πf = 2π * 300 =1884 (с^-1)

Находим реактивное сопротивление на всех элементах цепи.

X_L1 = ωL₁ = 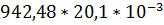= 37,888(Ом);

X_L3 = ωL₃ = 942,48 * 0* 10^-3 = 0 (Ом)

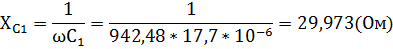
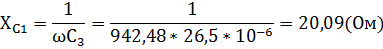
Комплексы действующих значений ЭДС:

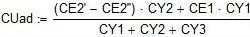
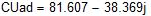
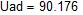
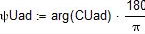
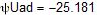
Комплексы и действующие значения начальной фазы ЭДС