Особенности процессов наращения и дисконтирования
В любой простейшей финансовой сделке всегда присутствуют три основных величины (текущая стоимость, будущая стоимость и процентная ставка), две из которых заданы, а одна из них является искомой.
Процесс, в котором заданы исходная денежная сумма и процентная ставка и совершаются над ними определенные действия, называется в финансовых расчетах процессом наращения. Под наращением понимают процесс увеличения первоначальной денежной суммы в результате начисления на нее процентов.
Экономический смысл метода наращения состоит в определении величины, которая будет или может быть получена из некоторой первоначальной (текущей) суммы в результате проведения определенной финансовой операции. Другими словами, метод наращения позволяет определить будущую величину (future value) текущей суммы (present value) через некоторый промежуток времени исходя из заданной процентной ставки.
В ряде случаев могут применяться неодинаковые способы подсчета числа дней в году (в соответствии с соглашением по подсчету дней между заинтересованными сторонами). Год может приниматься равным 365 или 360 дням.
Если временная база принимается равной 365 дням, то проценты называются точными. Если временная база равна 360 дням, то принято говорить о коммерческих, или обыкновенных, процентах. В свою очередь подсчет длительности ссуды может быть или приближенным, когда исходят из продолжительности года в 360 дней, или точным - по календарю. Определяя приближенную продолжительность ссуды, сначала подсчитывают число полных месяцев, затем умножают его на 30. Далее добавляют число дней, которые имеют место в неполных месяцах. Общим для всех способов подсчета является правило: день выдачи, идень возврата кредита считаются за один день (граничный день).
Наиболее часто встречаются следующие комбинации временной базы и длительности ссуды (цифры в скобках обозначают соответственно величину продолжительности года в днях и количество дней пользования ссудой):
1. Точные проценты с точным числом дней (365 / 365).
2. Обыкновенные (коммерческие) проценты с точной длительностью ссуды (365 / 360).
3. Обыкновенные (коммерческие) проценты с приближенной длительностью ссуды (360 / 360).
Различия в способах подсчета дней могут показаться несущественными. Однако при больших суммах и высоких процентных ставках эти различия достигают весьма значительных размеров.
Пример.
Предположим, что ссуда в размере 10 млн. руб. выдана 1 мая с возвратом 31 декабря этого же года под 45% годовых (простая процентная ставка). Определим наращенную сумму этого кредита по каждому из трех способов. Табличное значение точной длительности ссуды равно 244 дням (365 - 121); приближенная длительность - 241 день (6 * 30 + 30 + 30 + 1):
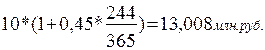 (51)
(51)
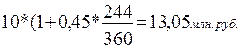 (52)
(52)

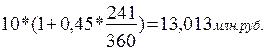 (53)
(53)
Полученная разница, имеющая место между наибольшей и наименьшей величинами (13,05 - 13,008), означает, что заемщик должен будет заплатить дополнительно 42 тыс. руб. только за то, что согласился на применение второго способа начисления процентов.
Обратной задачей по отношению к начислению процентов является расчет современной стоимости будущих денежных поступлений (притоков) или дисконтирование.
Вообще слово дисконтирование означает предпочтение инвесторами (хозяйствующими субъектами) вложений средств (капитальных вложений) в настоящее время ради будущих доходов и одновременно математический прием, позволяющий выразить это предпочтение. Буквальный перевод этого слова с английского (discounting) означает «снижение стоимости, уценка».
Дисконтирование представляет собой процесс нахождения некоторой величины денежных средств на заданный момент времени по ее известному или предполагаемому значению в будущем. В экономическом смысле будущая величина денежных средств, найденная в процессе дисконтирования, показывает современное (с позиции текущего момента времени) значение этой будущей величины.
Дисконтирование является зеркальным отражением процедуры наращения. Используемую при этом процентную ставку называют нормой дисконта или показателем дисконтирования.
В зависимости от того, какая именно ставка - простая процентная или простая учетная - применяется для дисконтирования, различают два его вида: математическое дисконтирование и банковский учет.
Метод банковского учета получил свое название от одноименной финансовой операции, в ходе которой коммерческий банк выкупает у владельца (учитывает) простой или переводный вексель по цене ниже номинала до истечения означенного на этом документе срока его погашения. Разница между номиналом и выкупной ценой образует прибыль банка от этой операции и называется дисконтом. Для определения размера выкупной цены (следовательно, и суммы дисконта) применяется дисконтирование по методу банковского учета. При этом используется простая учетная ставка.
Пример.
Пусть владелец векселя номиналом 25 000 руб. обратился в банк с предложением учесть его за 60 дней до наступления срока погашения. Банк согласен выполнить эту операцию по простой учетной ставке 35% годовых. Выкупная цена векселя составит:
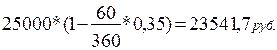 (54)
(54)
Сумма дисконта будет равна: 25 000 - 23 541,7 = 1458,3 руб.
Метод математического дисконтирования по простым процентам применяется во всех остальных (кроме банковского учета) случаях, когда возникает необходимость определить современную величину суммы денег, которая будет получена в будущем.
Пример.
Покупатель обязуется оплатить поставщику стоимость закупленных товаров через 90 дней после поставки в сумме 1 млн. руб. Уровень простой процентной ставки составляет 30% годовых (обыкновенные проценты). Следовательно, текущая стоимость товаров будет равна
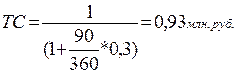 (55)
(55)
Применив к этим условиям метод банковского учета, получим:
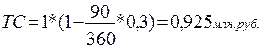 (56)
(56)
Применив к этим условиям метод банковского учета, получим, что второй вариант оказывается более выгодным для кредитора. Следует помнить, что каких - либо жестких требований выбора того или иного метода выполнения финансовых расчетов не существует. Никто не может запретить участникам финансовой операции выбрать в данной ситуации метод математического дисконтирования или банковского учета. Существует единственная закономерность: банками, как правило, выбирается метод, более выгодный для кредитора (инвестора).
Если при наращении речь идет о движении денежного потока от настоящего времени к будущему, то это именуется иногда процессом капитализации, а во втором случае движение от будущего денежного потока к настоящему именуется процессом дисконтирования.
В результате осуществления процедур наращения и дисконтирования осуществляется приведение денежных сумм, относящихся к различным временным периодам, к моменту времени в настоящем или будущем.
