Линейные регрессионные модели
Регрессионный анализ – это статистический метод исследования функциональной связи случайной величины y от переменных 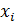 ,
, 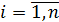 , рассматриваемых как неслучайные (известные) многомерные случайные величины с произвольной функцией распределения.
, рассматриваемых как неслучайные (известные) многомерные случайные величины с произвольной функцией распределения.
Задачей регрессионного анализа является построение зависимости изучаемой случайной величины y от факторов x по результатам наблюдения:
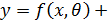 ξ, (1.4)
ξ, (1.4)
где 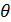 – неизвестные параметры, ξ– случайные ошибки или остатки,
– неизвестные параметры, ξ– случайные ошибки или остатки, 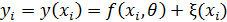 – независимые наблюдения,
– независимые наблюдения, 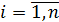 [27].
[27].
Регрессионные модели бывают линейными и нелинейными. В линейной регрессионной модели математическое ожидание зависимой переменной – это линейная комбинация регрессоров с неизвестными коэффициента, что функция 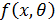 линейна по параметрам. Уравнение линейной регрессии записывается следующим образом:
линейна по параметрам. Уравнение линейной регрессии записывается следующим образом:
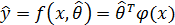 , (1.5)
, (1.5)
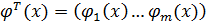 – известные функции,
– известные функции, 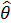 – оценка параметров регрессии.
– оценка параметров регрессии.
Будем рассматривать линейные оценки истинных параметров. Можно найти оценки 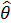 , которые являются состоятельными, несмещенными и обладают наименьшими дисперсиями среди множества всех линейных несмещенных оценок [27]. Такие оценки называются наилучшими линейными оценками, и в случае независимых и распределенных с одинаковыми дисперсиями случайными ошибками ξ вычисляются по формуле:
, которые являются состоятельными, несмещенными и обладают наименьшими дисперсиями среди множества всех линейных несмещенных оценок [27]. Такие оценки называются наилучшими линейными оценками, и в случае независимых и распределенных с одинаковыми дисперсиями случайными ошибками ξ вычисляются по формуле:
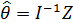 , (1.6)
, (1.6)
где матрица 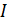 равна
равна
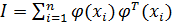 , (1.7)
, (1.7)
матрица 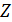 равна
равна
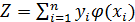 . (1.8)
. (1.8)
Средний квадрат ошибки прогноза равен
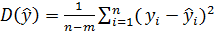 . (1.9)
. (1.9)
Ковариационная матрица ошибок оценок 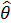 равна
равна
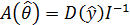 . (1.10)
. (1.10)
Ширина коридора ошибок в данном случае определяется по формуле:
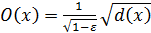 , (1.11)
, (1.11)
где ε – уровень доверия, а 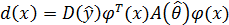
Для оценивания точности регрессионной модели используют коэффициент детерминации. Коэффициентом детерминации называется число:
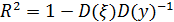 . (1.12)
. (1.12)
Коэффициент детерминации определяет наличие функциональной связи вида (1.9). Если 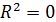 , то
, то 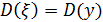 , то есть неучтенные ошибки будут определяющими. Следовательно, линейная связь между
, то есть неучтенные ошибки будут определяющими. Следовательно, линейная связь между 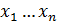 и
и 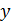 отсутствует. Если
отсутствует. Если 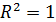 , то
, то 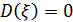 , то вектор
, то вектор 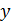 однозначно определяется переменными
однозначно определяется переменными 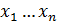 . Если
. Если 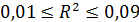 , то связь между
, то связь между 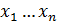 и
и 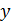 недостаточно подтвержденная. Если
недостаточно подтвержденная. Если 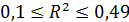 , то говорят о наличии средней связи. При
, то говорят о наличии средней связи. При 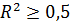 , применение линейной регрессии обосновано и связь сильная [27].
, применение линейной регрессии обосновано и связь сильная [27].
Факторный анализ
Факторный анализ является естественным обобщением и развитием метода главных компонент. Если объект описывается с помощью n признаков, то в результате действия метода получается математическая модель, зависящая от меньшего числа переменных. При этом предполагается, что на исходные измеряемые данные 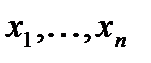 оказывает влияние небольшое число латентных признаков. Цель факторного анализа заключается в выявлении этих скрытых характеристик (факторов) и оценивании их числа.
оказывает влияние небольшое число латентных признаков. Цель факторного анализа заключается в выявлении этих скрытых характеристик (факторов) и оценивании их числа.
Запишем факторную модель в общем виде
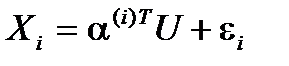 , (1.13)
, (1.13)
где 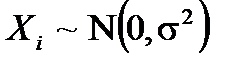 ,
, 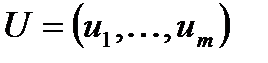 – факторы,
– факторы, 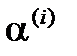 – факторные нагрузки,
– факторные нагрузки, 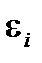 – латентные факторы,
– латентные факторы, 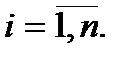
Техника факторного анализа направлена на определение факторных нагрузок, дисперсий характерных факторов и значений факторов для каждого наблюдаемого объекта.
Запишем двухфакторную модель в виде:
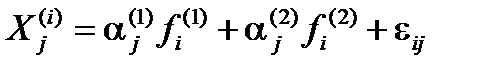 ,
, 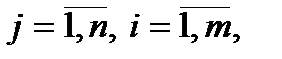
причем на 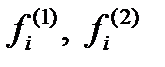 накладывают условие взаимной некоррелированности
накладывают условие взаимной некоррелированности 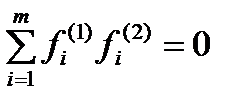 и условие нормировки
и условие нормировки 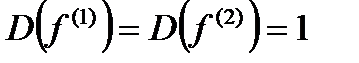 .
.
Нахождение факторных нагрузок и факторов осуществляется с помощью метода неопределенных множителей Лагранжа из условия минимизации 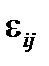 . Так как
. Так как 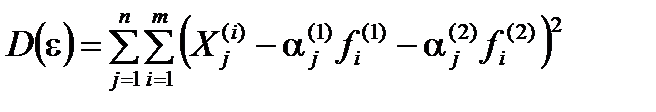 , то функция Лагранжа определяется следующим равенством:
, то функция Лагранжа определяется следующим равенством:
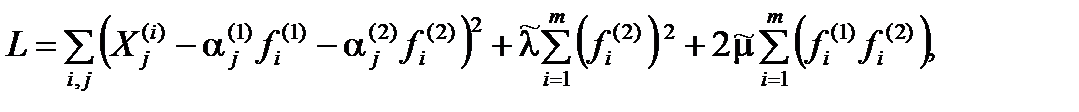 где
где 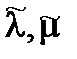 – неизвестные множители.
– неизвестные множители.
Для нахождения условного экстремума дифференцируем функцию Лагранжа по 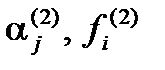 и приравниваем найденные производные нулю:
и приравниваем найденные производные нулю:
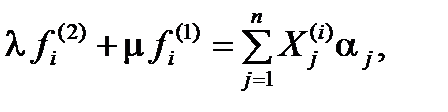
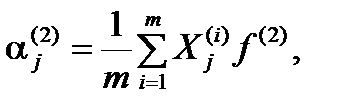 (1.14)
(1.14)
где 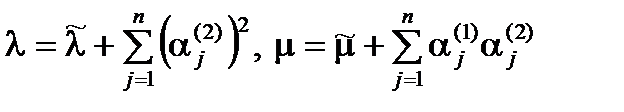 .
.
Можно показать, что 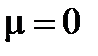 . Тогда имеет место случай однофакторной модели, причем за фактор взят вектор
. Тогда имеет место случай однофакторной модели, причем за фактор взят вектор 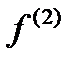 . Решение этой задачи известно:
. Решение этой задачи известно: 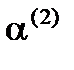 – собственные вектора матрицы ковариаций
– собственные вектора матрицы ковариаций 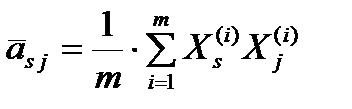 ,
, 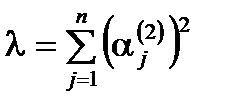 – ее собственные числа. При этом дисперсия
– ее собственные числа. При этом дисперсия 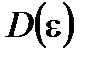 достигает минимума, если
достигает минимума, если 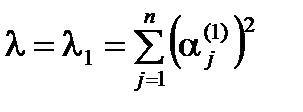 и
и 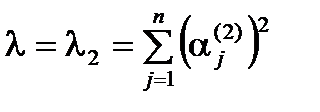 будут первым и вторым наибольшими по величине собственными числами матрицы
будут первым и вторым наибольшими по величине собственными числами матрицы 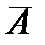 .
.
Вводя в рассмотрение матрицу P c центрированными элементами исходных данных по формуле 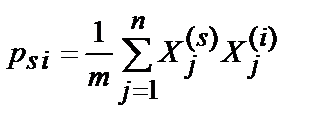 и учитывая выполнение соотношения
и учитывая выполнение соотношения 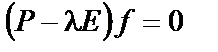 , полученного ранее в однофакторной модели, определим факторы
, полученного ранее в однофакторной модели, определим факторы 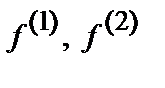 как собственные вектора матрицы P, соответствующие ее первым максимальным по абсолютной величине собственным числам
как собственные вектора матрицы P, соответствующие ее первым максимальным по абсолютной величине собственным числам 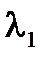 и
и 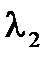 .
.
Рассмотрение общего случая p–факторной модели производится в полном соответствии с двухфакторной моделью. Однако следует помнить, что при вычислении факторов и факторных нагрузок необходимо задействовать уже p наибольших по величине собственных чисел и p соответствующих им собственных векторов.
Найденные 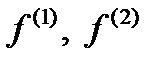 образуют в пространстве признаков новый базис, а
образуют в пространстве признаков новый базис, а 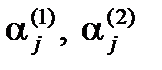 играют роль координат
играют роль координат 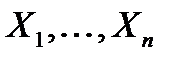 в этом базисе.
в этом базисе.
После определения факторов исследователю зачастую требуется оценить уровень информативности или вклад фактора в суммарную дисперсию всех признаков.
Определение: пусть имеется n-факторная модель. Пусть 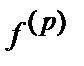 – некоторый фактор,
– некоторый фактор, 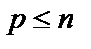 . Вкладом фактора
. Вкладом фактора 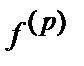 в суммарную дисперсию всех признаков называется число
в суммарную дисперсию всех признаков называется число 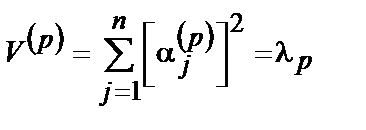 , где
, где 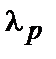 – собственное число выборочной матрицы ковариаций
– собственное число выборочной матрицы ковариаций 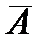 .
.
Очевидно, что для n-факторной модели общая дисперсия есть 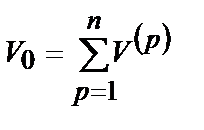 . В этом случае
. В этом случае 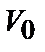 называют еще суммарной общностью факторов
называют еще суммарной общностью факторов 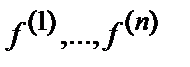 .
.
Определение: долей фактора 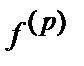 в суммарной общности называется отношение
в суммарной общности называется отношение 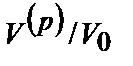 . Оно характеризует долю, которую вносит фактор
. Оно характеризует долю, которую вносит фактор 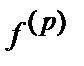 в факторную модель.
в факторную модель.
Определение: пусть 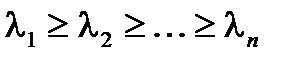 – собственные числа выборочной матрицы ковариаций
– собственные числа выборочной матрицы ковариаций 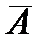 . Пусть собственному числу
. Пусть собственному числу 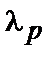 соответствует фактор
соответствует фактор 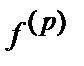 и имеются факторные нагрузки
и имеются факторные нагрузки 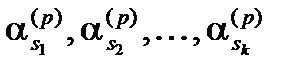 , которые, в свою очередь, являются наибольшими по абсолютной величине координатами вектора
, которые, в свою очередь, являются наибольшими по абсолютной величине координатами вектора 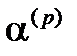 . Тогда число
. Тогда число 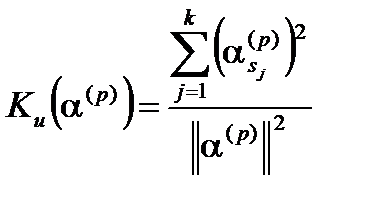 называется коэффициентом информативности признаков
называется коэффициентом информативности признаков 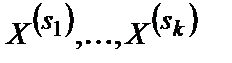 .
.
Данное число определяет, какие вектора из множества 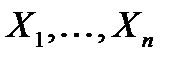 вносят наибольший вклад в название
вносят наибольший вклад в название 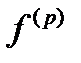 . Принято считать набор объясняющих признаков
. Принято считать набор объясняющих признаков 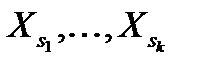 удовлетворительным, если
удовлетворительным, если 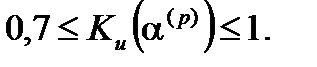 [21]
[21]
