Концепция оценки стоимости денег во времени

Инвестиционный менеджмент требует постоянного осуще­ствления различного рода финансово-экономических расчетов, связанных с денежными потоками в разные периоды времени. Главную роль в этих расчетах играет оценка стоимости денег во времени.

В условиях рыночной экономики при осуществлении инве­стиций и проведении финансовых операций фактор времени играет важную роль для обеспечения достоверности и объек­тивности расчетов, связанных с оценкой эффективности инве­стиционных проектов. Золотое правило бизнеса состоит в том, что «одинаковая сумма, полученная сегодня, больше той сум­мы, которая будет получена завтра».

Неравноценность одних и тех же сумм, полученных в раз­ные периоды времени, объясняется следующим образом:

• инвестированная сумма свободных денежных средств обусловит получение дохода в будущем;

• под воздействием инфляции покупательная стоимость де­нег с течением времени снижается.

Исходя из этого, из теории временной ценности денег выте­кают два важных следствия:

• необходимость учета фактора времени при расчетах эф­фективности инвестиций;

• некорректность простого суммирования денежных пото­ков, относящихся к разным периодам.

Концепция оценки стоимости денег во времени заключа­ется в том, что стоимость денег во времени изменяется с уче­том нормы прибыли на финансовом рынке, в качестве которой выступает норма ссудного процента. Концепция стоимости де­нег во времени рассматривается в двух аспектах.

Первый аспект связан с покупательной способностью денег. Денежные средства в данный момент и через определенный промежуток времени при равной номинальной стоимости име­ют разную покупательную стоимость. Так, 1000 руб. через ка­кое-то время при уровне инфляции 10% будут иметь покупа­тельную способность лишь 900 руб.

Второй аспект связан с обращением денежных средств как капитала и получением доходов от этого оборота.

В целом неравноценность разновременных затрат и резуль­татов любой финансовой операции обычно проявляется в том, что получение дохода сегодня считается более предпочтитель­ным, чем получение дохода завтра, а расходы сегодня менее предпочтительны, чем расходы завтра.

Понятие временной стоимости денег приобрело особую ак­туальность в нашей стране с началом перехода к рыночной экономике. Причин было несколько: инфляция, расширив­шиеся возможности вложения временно свободных средств, снятие всевозможных ограничений в отношении формирова­ния финансовых ресурсов хозяйствующими субъектами. Все это связано с тем, что деньги, помимо прочего, имеют еще одну объективно существующую характеристику — времен­ную ценность.

В наиболее общем смысле понятие «временная ценность де­нег» означает, что рубль, имеющийся в распоряжении сегодня, и рубль, ожидаемый к получению в будущем, не равны.

Разность в оценке текущих денежных средств и той же их суммы в будущем может быть вызвана:

• негативным воздействием инфляции, в связи с чем проис­ходит уменьшение покупательной способности денег;

• возможностью альтернативного вложения денежных средств и их реинвестирования в будущем (фактор упу­щенной выгоды).

Оценка стоимости денег с учетом фактора времени требует предварительного рассмотрения связанных с ней базовых по­нятий.

Процент — сумма дохода от предоставления капитала в долг или плата за пользование ссудным капиталом во всех его формах (депозитный процент, кредитный процент, процент по облигациям, процент по векселям и т.п.).

Простой процент — сумма дохода, начисляемого к основ­ной сумме капитала в каждом интервале, по которой дальней­шие расчеты платежей не осуществляются. Начисление про­стого процента применяется, как правило, при краткосрочных финансовых операциях.

Сложный процент — сумма дохода, начисляемого в каж­дом интервале, которая не выплачивается, а присоединяется к основной сумме капитала и в последующем платежном перио­де сама приносит доход. Начисление сложного процента при­меняется, как правило, при долгосрочных финансовых опера­циях (инвестирование, кредитование).

Процентная ставка — удельный показатель, в соответст­вии с которым в установленные сроки выплачивается сумма процента в расчете на единицу капитала.

Будущая стоимость денег — сумма инвестированных в на­стоящий момент денежных средств, в которую они превратятся через определенный период времени с учетом определенной процентной ставки.

Настоящая стоимость денег — сумма будущих денежных средств, приведенных с учетом определенной процентной став­ки к настоящему периоду времени.

Наращение стоимости (компаундинг) — процесс приве­дения настоящей стоимости денег к их будущей стоимости в определенном периоде путем присоединения к их первоначаль­ной сумме начисленной суммы процентов.

Дисконтирование стоимости — процесс приведения буду­щей стоимости денег к их настоящей стоимости путем изъятия из их будущей суммы соответствующей суммы процентов.

Период начисления — общий период времени, в течение ко­торого осуществляется процесс наращения или дисконтирова­ния стоимости денежных средств.

Интервал начисления — обусловленный конкретный вре­менной срок, в рамках которого рассчитывается отдельная сум­ма процента по установленной его ставке.

Предварительный метод начисления процента (метод ^пренумерандо) — способ расчета платежей, при котором на­числение процента осуществляется в начале каждого интерва­ла.

Последующий метод начисления процента (метод пост-Щмерандо) — способ расчета платежей, при котором начисление процента осуществляется в конце каждого интервала.

Дискретный денежный поток — поток платежей на вло­женный капитал, имеющий четко ограниченный период начис­ления процентов и конечный срок возврата основной его сум­мы.

Непрерывный денежный поток — поток платежей на вло­женный капитал, период начисления процентов по которому не ограничен, а соответственно не определен и конечный срок возврата основной его суммы.

Аннуитет (финансовая рента) — длительный поток пла­тежей, характеризующийся одинаковым уровнем процентных ставок на протяжении всего периода.

Система основных базовых понятий позволяет последова­тельно рассмотреть методический инструментарий оценки стоимости денег. Реализация инвестиционного проекта осуще­ствляется в течение определенного периода времени, между вложением средств и отдачей в виде чистого денежного потока неизбежен разрыв, так называемый временной лаг, который не­обходимо учитывать.

Поэтому для оценки ожидаемых финансовых результатов разных периодов времени применяют метод дисконтирования и наращения — приведение денежных сумм в сопоставимый вид по фактору времени. По экономической сути операция дисконтирования обратна процессу наращения (рис. 5.1).

Наращение Д х (1 + Е)^t

Периоды планирования		2			t
Ожидаемые результаты	Да	д2	Дз		Дг

Д/ (1 + Е)^t Дисконтирование

Рис. 5.1. Учет фактора времени в финансовых расчетах

Дисконтированные показатели рассчитывают с учетом не­равноценности результатов и затрат инвестиционного проекта во времени. Разновременные денежные потоки приводят в со­поставимое значение путем дисконтирования.

5.2- Методы начисления простых и сложных процентов

В зависимости от условий проведения расчетов оценки эффективности инвестиционных проектов как дисконтирование, так и наращение осуществляются с применением простых и сложных процентов.

Простые проценты в практике используются в краткосрочных финансовых операциях сроком менее одного года, когда используется наиболее упрощенная система расчетных алгоритмов.

Базой для исчисления процентов за каждый плановый период при простых процентах является первоначальная (исходная) сумма сделки. Схема простых процентов предполагает неизменность базы, с которой происходит начисление.

1. Будущая стоимость вклада К6 с учетом начисленной суммы процента через t лет определяется по формуле

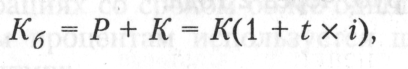
где Р — сумма процента за обусловленный период времени в целом;

К — первоначальная сумма денежных средств; t — количество интервалов, по которым осуществляется расчет процентных платежей; i — процентная ставка.

Множитель (1 + t х г) называется множителем наращения суммы простых процентов. Его значение всегда должно быть больше единицы.

Сумма простого процента в процессе наращения стоимости капитала рассчитывается по формуле

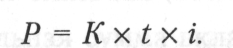
Пример. Определить будущую стоимость вклада и сумму простого процента за год при следующих условиях: первоначальная сумма вклада — 5000 руб.; процентная ставка, выплачиваемая ежеквартально, — 3%. Решение:

сумма процента составит

Р - 5000 х 4 х 0,03 = 600 руб.;

К - 5000(1 + 4 х 0,03) = 5600 руб.

Пример. Определить период начисления при годовой процентной ставке г = 0,1, за который первоначальный капитал 100 тыс. руб. вырастет до 140 тыс. руб. по простым процентам.

Решение:

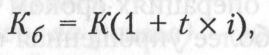
отсюда

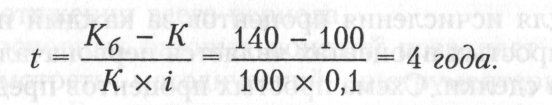
Пример. Рассчитать простую ставку процентов (i), при которой первоначальный капитал (К) в размере 200 тыс. руб. достигнет 230 тыс. руб. через 2 года.

Решение:

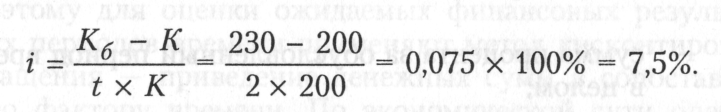
2. Настоящая стоимость денежных средств Кн с учетом начисленной суммы простого процента определяется по формуле

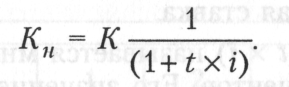
Множитель 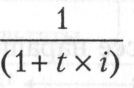называется дисконтным множителем

суммы простых процентов, значение которого всегда должно быть меньше единицы.

Сумма простого процента в процессе дисконтирования стоимости определяется по формуле

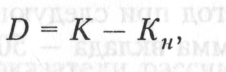
где D — величина дисконта за обусловленный период времени в целом; К — первоначальная сумма денежных средств.

Пример. Определить настоящую (текущую) стоимость вклада и сумму дисконта по простому проценту за год при следующих условиях:

конечная сумма вклада — 5000 руб.;

дисконтная ставка, выплачиваемая ежеквартально, — 3%. Решение:

настоящая стоимость вклада составит

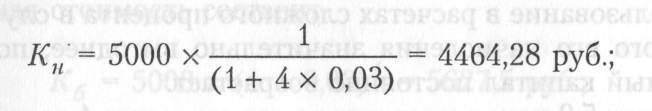
начисленная сумма дисконта составит

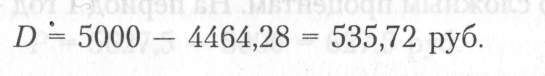
Сложные проценты широко применяются в долгосрочных финансовых операциях со сроком более одного года. Для расчета по сложным процентам используется широкая система расчетных алгоритмов.

Базой для исчисления процентов за каждый плановый период при сложных процентах являются первоначальная (исходная) сумма сделки и к этому времени накопленные проценты.

1. При расчете будущей суммы вклада в процессе его наращения по сложным процентам используется следующая формула:

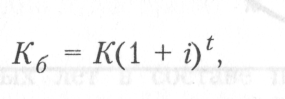
где Кб — будущая стоимость вклада по сложным процентам;

К — первоначальная сумма вклада; t — количество интервалов, по которым осуществляется расчет процентных платежей; i — процентная ставка.

Соответственно начисленная сумма процента Р определяется по формуле

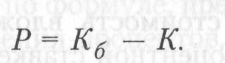
Таким образом, если инвестиция осуществлена на условиях сложного процента, то годовой доход по определенной годовой ставке исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей ранее начисленные и невостребованные инвестором проценты. В этом случае проис­ходит капитализация процентов по мере их начисления, т.е. ис­ходная база все время возрастает.

Использование в расчетах сложного процента в случае мно­гократного его начисления значительно выгоднее, поскольку вложенный капитал постоянно возрастает.

Рисунок 5.2 показывает, что за период менее 1 года выгодно вкладывать капитал по простым процентам. За период более 1 года — по сложным процентам. На период 1 год — одинаково.

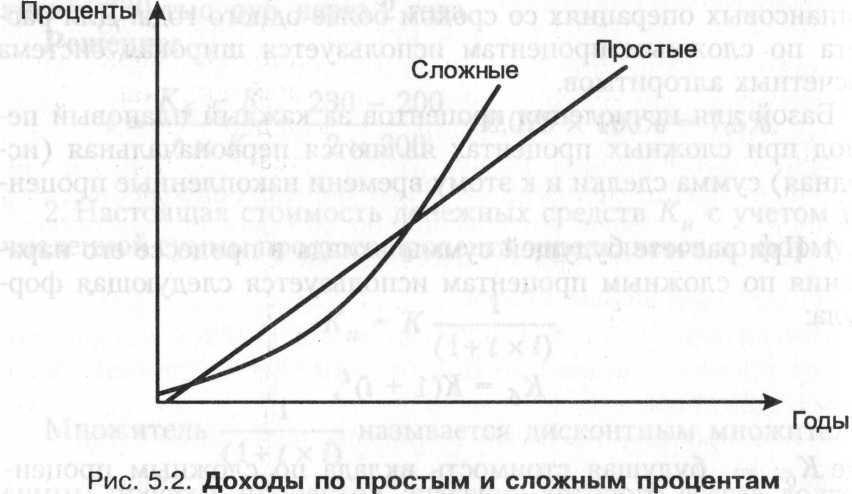
Формула сложных процентов используется при оценке эф­фективности инвестиционных проектов. Выражение (1 + i) называют мультиплицирующим множителем или множителем наращения сложных процентов.

Экономический смысл множителя состоит в следующем: он показывает будущую стоимость вложенного капитала через п лет при заданной процентной ставке i.

Пример. Определить будущую стоимость вклада и сумму сложного процента за весь период инвестирования при сле­дующих условиях:

первоначальная стоимость вклада — 5000 руб.;

процентная ставка, выплачиваемая ежеквартально, — 3%;

общий период инвестирования — 1 год.

решение:

будущая стоимость составит

К_б - 5000 х (1 + 0,03)⁴ - 5627,5 руб.;

начисленная сумма процента равна

. Р = 5627,5 - 5000 = 627,5 руб.

При вложении капитала на депозитный счет может быть си­туация, когда срок операции составляет не целое число лет. В этом случае кредиторы используют смешанный порядок начис­ления процентов: сложные проценты начисляются на период, измеренный целыми годами, а проценты за дробную часть сро­ка начисляются по простой процентной ставке. Тогда будущая (наращенная) стоимость вложенного капитала определяется по формуле

К_б = К(1+i)^t х (1+ )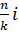

где t — число полных лет в составе продолжительности операции;

п — число дней в отрезке времени, приходящемся нанеполный год; k— временная база.

Пример. Инвестор вкладывает 100 тыс. руб. на депозитный счет банка под 12% годовых. Действие договора распространя­йся на период с 1 июня 2006 г. по 31 декабря 2009 г. Опреде­лить будущую стоимость первоначального капитала по форму-^Ле сложных процентов и по формуле, предусматривающей сме­шанный порядок исчисления процентов.

Решение:

в случае начисления сложных процентов за весь срок договора

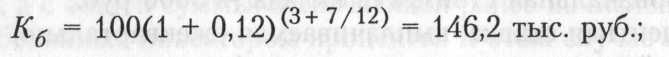
при смешанном способе

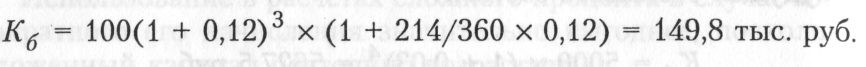
Таким образом, при смешанном методе начисления процентов инвестор получит на 3,6 тыс. руб. больше.

2. При расчете настоящей стоимости денежных средств в процессе дисконтирования Кн по сложным процентам используется следующая формула: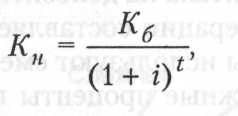

где К_н — будущая сумма вклада;

t — количество интервалов, по которым осуществляется расчет процентных платежей;

i — процентная ставка.

Соответственно начисленная сумма дисконта D определяется по формуле

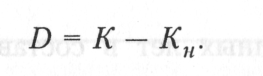
Пример. Определить настоящую стоимость денежных средств и сумму дисконта по сложным процентам за 1 год при следующих условиях:

будущая стоимость вклада — 5000 руб.;

процентная ставка, выплачиваемая ежеквартально, — 3%.

Решение:

настоящая стоимость вклада составит

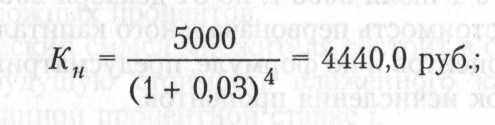
начисленная сумма дисконта

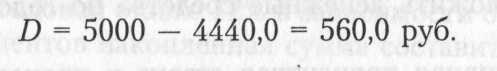
3. Для определения процентной ставки, используемой в рас­четах стоимости денежных средств по сложным процентам, применяется следующая формула:

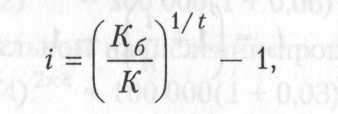
где i — процентная ставка;

К_б — будущая стоимость вклада при его наращении по сложным процентам;

К — первоначальная сумма денежных средств;

t — количество интервалов, по которым осуществля­ется расчет процентных платежей.

Пример. Определить годовую ставку доходности облигации при следующих условиях:

номинал облигации, подлежащей погашению через 3 года, составляет 5000 руб.;

цена, по которой облигация реализуется в момент ее эмис­сии, составляет 3000 руб.

Решение:

годовая ставка доходности составит

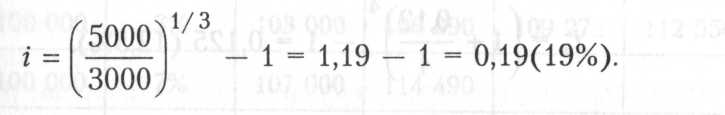
Пример. Инвестор имеет 300 000 руб. и желает получить че­рез 2 года 400 000 руб. Каково в этом случае должно быть ми­нимальное значение годовой процентной ставки?

Решение:

пользуемся формулой

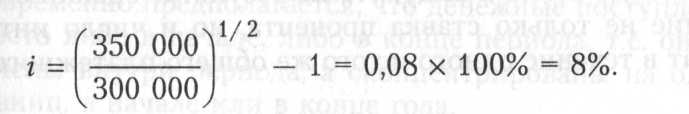
Следовательно, для того чтобы получить необходимую сум­му, нужно вложить денежные средства по годовой ставке не ниже 8%.

4. Эффективная процентная ставка в процессе наращения стоимости денежных средств по сложным процентам рассчи­тывается по формуле

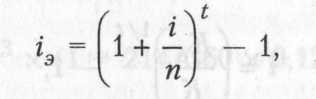
где г_э — эффективная среднегодовая процентная ставка при наращении стоимости денежных средств по сложным процентам; i — процентная ставка, используемая при наращении стоимости денежных средств по сложным процен­там.

Пример. Определить эффективную среднегодовую про­центную ставку при следующих условиях:

денежная сумма 5000 руб. помещена в коммерческий банк на депозит сроком на 2 года;

годовая процентная ставка, по которой ежеквартально осу­ществляется начисление процента, составляет 12%.

Решение:

эффективная среднегодовая процентная ставка составит

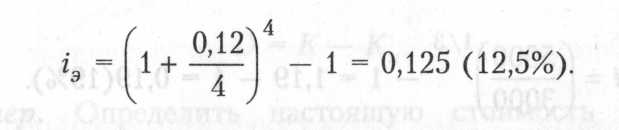
Результаты расчетов показывают, что условия размещения вклада на 2 года под 12% годовых при ежеквартальном начис­лении процентов равнозначны условиям начисления этих про­центов 1 раз в год под 12,5% годовых.

При оценке стоимости денег во времени по сложным про­центам надо иметь в виду, что на результат оценки оказывает влияние не только ставка процента, но и число интервалов выплат в течение одного и того же общего платежного перио­да.

Пример. Если вклад в сумме 100 ООО руб. хранить в банке 2 года, то при годовой ставке 12% в зависимости от частоты на­числения процентов накопленная сумма составит:

а) при начислении процента 1 раз в год 100 000(1 + 0,12)² = 125 440,0 руб.;

б) при полугодовом начислении процентов

100 000(1 + 0,12/2)^2x2 = 100 000(1 + 0,06)⁴ = 126 247,69 руб.;

в) при ежеквартальном начислении процентов

100 000(1 + 0,12/4)^2x4 = 100 000(1 + 0,03)⁸ = 126 677,0 руб.;

г) при ежемесячном начислении процентов

100 000(1 + 0,12/12) ^2х12=100 000(1 + 0,01) ²⁴=126 973,46 руб.

Пример. Перед инвестором стоит задача разместить 100 тыс. руб. на депозитный вклад сроком на 1 год. Первый банк предлагает инвестору выплачивать доход по сложным процентам в размере 3% в квартал; второй — в размере 7% 2 раза в год, третий — 13% 1 раз в год. Определить, какой вари­ант лучше. Результаты расчетов приведены в табл. 5.1.

Таблица 5.1

Вари­анты	Настоя­щая стои­мость вклада	Про­центная ставка	Будущая стоимость вклада в конце периода
			1-го	2-го	3-го	4-го
1-й	100 000	3%	103 000	106 090	109 272	112 550
2-й	100 000	7%	107 000	114 490
3-й	100 000	13%	113 000

Второй вариант лучший.

Временные периоды, которым соответствуют определенные по величине денежные потоки, обычно предполагаются равны­ми. Одновременно предполагается, что денежные поступления имеют место либо в начале, либо в конце периода, т.е. они не Распределены внутри периода, а сконцентрированы на одной из его границ, в начале или в конце года.

Поступления в начале года называются потоком пренуме-рандо или авансом, в конце года — постнумерандо.

Разница между ними состоит в том, что в первом случае поступление денежных средств происходит параллельно с вложением инвестиций.

На практике относительно большее распространение получил поток постнумерандо, поскольку финансовые результаты определяются обычно по окончании очередного отчетного года. Именно этот поток положен в основу методик анализа эффективности инвестиционных проектов. Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования.

5.3. Методика оценки стоимости денег при аннуитете

Ряд последовательных фиксированных платежей, производимых через равные промежутки времени, называют финансовой рентой, или аннуитетом.

Аннуитет — во-первых, это один из видов срочного займа, по которому ежегодно выплачиваются проценты и погашается часть суммы; во-вторых, так называют равные друг другу денежные платежи, выплачиваемые через равные промежутки времени в счет погашения полученного кредита, займа, и проценты к ним. В основном это вложение денежных средств в страховые и пенсионные фонды. Страховые компании и пенсионные фонды выпускают долговые обязательства, которые их владельцы хотят использовать на покрытие непредвиденных расходов в будущем. Пенсионные фонды обеспечивают своих клиентов денежными средствами на период после выхода на пенсию.

Аннуитет рассчитывается с помощью коэффициента аннуитета (Кан), который распределяет величину К0 на равные суммы платежей с учетом процента на t лет, т.е. превращает «разовый платеж сейчас» в платежный ряд.

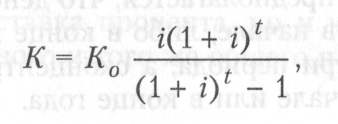
где Ко — ежегодный взнос денежных средств, тыс. руб.;

К — накопленная сумма, тыс. руб.;

i — годовая процентная ставка;

t — период потока платежей;

выражение

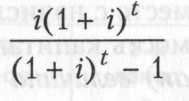
называется коэффициентом аннуитета.

Пример. Инвестор ежегодно в начале года (пренумерандо) делает взнос в размере 500 тыс. руб. под 12% годовых. Определить, какая сумма будет на счете по истечении 5 лет?

Решение:

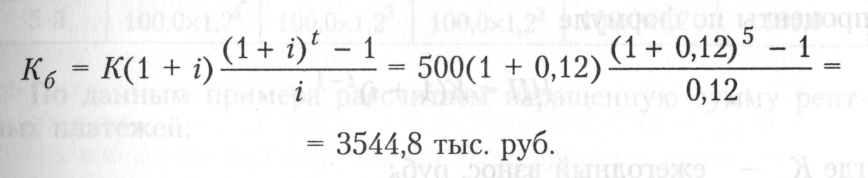
Пример. Коммерческий банк предоставил клиенту кредит на 3 года в размере 600 тыс. руб. под 16% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. По договору кредит возвращается равными суммами в конце каждого года (постнумерандо). Требуется рассчитать величину годового платежа.

Решение:

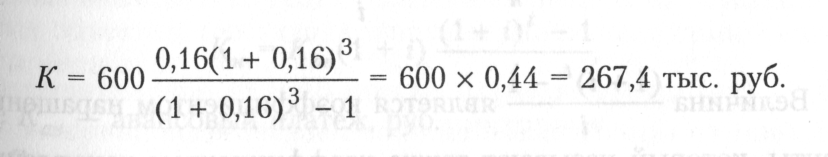
Оплата по заключенным сделкам может предусматривать как разовый платеж, так и ряд выплат, распределенных ро времени. Выплата арендной платы, выплаты за приобретенное имущество в рассрочку, инвестирование средств в различные программы и т.п. В большинстве случаев платежи производятся через определенные промежутки времени, т.е. образуется поток платежей.

Обобщающими показателями ренты являются: наращенная сумма и современная (текущая) величина потока платежей.

Наращенная сумма — это сумма всех членов потока платежей с начисленными на них процентами на конец срока, т.е. на дату последней выплаты. Наращенная сумма денежных средств, вносимых через равные промежутки времени в течение всего срока ренты вместе с начисленными процентами, показывает будущую стоимость капитала.

Современная (текущая) величина потока платежей — это сумма всех его поступлений, уменьшенная (дисконтированная) на величину процентной ставки за определенный момент времени, совпадающий с началом потока платежей или предшествующий ему.

Наращенная сумма ренты

На вносимые платежи в течение всего срока начисляются проценты по формуле

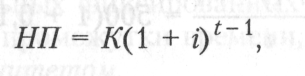
где К — ежегодный взнос, руб.; z — процентная ставка; t — период потока платежей.

Наращенная сумма к концу срока выплаты рентных платежей определяется по формуле

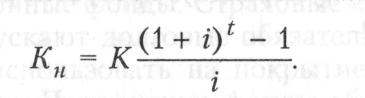
Величина 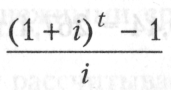является коэффициентом наращения

ренты, который называют также коэффициентом накопления денежной единицы за период.

Пример. Помещение сдается в аренду сроком на 5 лет. Арендные платежи в размере 100 тыс. руб. вносятся кредитором ежегодно в конце года в банк на счет владельца помещения. Банк на внесенные суммы начисляет проценты в расчете 20% годовых. Определите сумму, полученную владельцем по_ещения в конце срока аренды, при условии, что со счета день­ги не изымались. Примем обозначения: величина ежегодного взноса К процентная ставка z, срок аренды п.

Представим эту финансовую операцию следующей схемой (табл. 5.2).

Таблица 5.2

Период взноса, год	1-й взнос	2-й взнос	3-й взнос	4-й взнос	5-й взнос
1-й	100,0	-	-	—	—
2-й	100,0x1,2	100,0	-	-	-
3-й	100,0х1,22	100,0x1,2	100,0	-	-
4-й	100,0xi,23	100,0х1,22	100,0x1,2	100,0	-
5-й	100,0xl,24	100,0х1,23	100,0х1,22	100,0x1,2	100,0

По данным примера рассчитаем наращенную сумму рент­ных платежей:

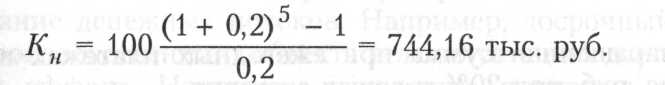
В случае если первый платеж производится немедленно, а последующие платежи производятся через равные интервалы (пренумерандо), такие ренты также называются авансовыми. Тогда сумма членов такой ренты вычисляется по формуле

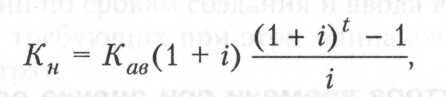
где К_ав — авансовый платеж, руб. Современная величина ренты

Современная величина ренты является суммой всех поступ­лений ренты, дисконтированных на момент приведения по вы­бранной ставке. Для ренты с ежегодными взносами К совре­менная величина (К_тек) вычисляется по формуле

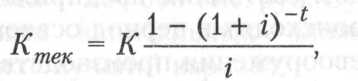
где 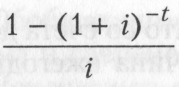дисконтированный множитель для аннуитета. Он показывает, чему равна с позиции текущего момента величина аннуитета с регулярными денежными поступлениями, продолжающегося t равных периодов с заданной процентной ставкой г.

Пример. Фирмой предусматривается создание в течение Злет фонда инвестирования в размере 1500 тыс. руб. Фирма имеет возможность ассигновать на эти цели ежегодно 412 тыс. руб., помещая их в банк под 20% годовых. Какая сумма потребовалась бы фирме для создания фонда в 1500 тыс. руб., если бы она могла поместить ее в банк одновременно на 3 года под 20% годовых?

Решение:

1) определяем текущую стоимость ежегодных взносов (Ктек) в течение 3 лет под 20% годовых

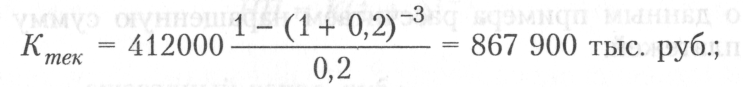
2) наращенная сумма при ежегодных платежах в размере 412 тыс. руб. под 20% годовых составит

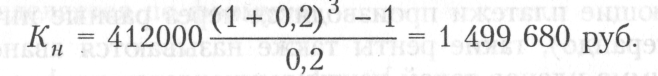
5.4. Учет фактора времени при оценке эффективности инвестиционных проектов

За период реализации и полезного использования инвестиционного проекта происходит изменение объема, структуры ассортимента и качества производимой продукции. Происходят изменения в численности и структуре персонала, в основных фондах, финансовом состоянии предприятия. Особенно сильные изменения происходят в период освоения новых изделий, технического перевооружения производств.

Под воздействием инфляции изменяются цены на произ­водственные и энергетические ресурсы, а также процентные ставки по кредитам. Учет влияния этих изменений осуществ­ляется путем построения денежных потоков по шагам расчета.

Исходя из этого, для решения задач оценки эффективности инвестиционного проекта необходимо обосновать теоретиче­ски возможность соизмерения единовременных и текущих за­трат и на этой основе возможность определения финансовых затрат во взаимосвязи с финансовыми результатами.

В соответствии с Методическими рекомендациями общий финансовый результат от инвестиционной деятельности пред­лагается определять путем суммирования операционных дохо­дов, полученных за весь срок использования инвестиционного проекта. Таким образом, определяется чистый доход от инве­стиционной деятельности. В состав доходов от операционной деятельности включается амортизация.

Сложившаяся теория оценки эффективности инвестиций исходит из предпосылки, что действие фактора времени на эф­фективность инвестиций происходит тогда, когда имеется лаг во времени.

Одним из способов учета фактора времени является дис­контирование денежных потоков. Например, досрочный ввод нового производственного объекта в эксплуатацию дает опре­деленный эффект. Напротив, увеличение плановых сроков ввода объекта вызывает замедление срока получения доходов.

Анализ практической деятельности научно-исследователь­ских, проектных и строительных организаций показывает, что могут существовать различные варианты распределения капи­тальных вложений по срокам создания и ввода в эксплуатацию новых объектов, требующих при этом одинаковой суммы еди­новременных затрат.

В этой ситуации лучшим считается тот вариант, при кото-Ром в первые годы затраты минимальные. В этом случае де­нежные средства заморожены на более короткий срок, и их можно направить на финансирование нового инвестиционного проекта.

Пример. Общий срок строительства — 3 года. Общая сумма капитальных вложений — 200 ООО тыс. руб. Существуют два ва­рианта распределения капитальных вложений по годам (^табл. 5.3). Определить лучший вариант.

Для решения поставленной задачи необходимо располагать информацией о нормативе эффективности капитальных вложений и о норме прибыли. Допустим, что банковский процент на денежные средства, положенные на депозитный счет, составляет 12%. Располагая данными о нормативе эффективности, задачу решаем двумя способами: методом дисконтирования и методом наращивания.

Таблица 5.3

Варианты	Распределение капитальных вложений по годам	Всего, тыс. руб.
1-й	2-й	3-й
1-й	100 000,0	60 000,0	40 000,0	200 000,0
2-й	30 000,0	70 000,0	100 000,0	200 000,0

Общая сумма приведенных затрат (Кпр) к расчетному году определяется по формуле

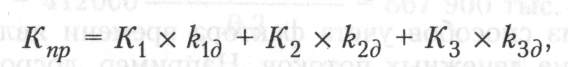
где Кр К2у К3 — капитальные вложения по годам строительства объекта, руб.; Кд> ^2д> ^Зд ~ коэффициенты дисконтирования. Коэффициенты дисконтирования по процентной ставке 12% составляют соответственно:

(1 + 0,12)° = 1,0; (1 + 0Д2)"1 = 0,893; (1 + 0,12)"2 = 0,797.

1) Кпр = 100 000 х 1 + 60 000 х 0,893 + 40 000 х 0,797 = = 100 000 + 53 600 + 31 900 = 185 500 тыс. руб.;

2) Кпр = 30 000 х 1 + 70 000 х 0,893 + 100 000 х 0,797 -- 30 000 + 62 500 + 79 700 = 172 200 тыс. руб.

Таким образом, эффективнее второй вариант, где меньше приведенные затраты.

Аналогичные результаты получаются, если решить задачу методом наращивания затрат.

Для расчета наращенных затрат используется следующая формула:

З_пр = К₁ х k_1н + К₂ х k_2н + К₃ х k_3н

где k_1н , k_2н,k_3н — коэффициенты наращивания.

Коэффициенты наращивания по процентной ставке 12% составляют соответственно:

(1 + 0Д2)2 = 1,254; (1 + 0Д2)1 - 1,12; (1 + 0,12)° = 1,0.

1) Зпр = 100 ООО х 1,254 + 60 000 х 1,12 + 40 000 х 1,0 -= 125 400 + 67 200 + 40 000 = 232 600 тыс. руб.;

2) Зп„ - 30 ООО х 1,254 + 70 000 х 1,12 + 100 000 х 1,0 = - 37 600 + 78 400 + 100 000 = 216 000 тыс. руб.

Естественно, также эффективнее второй вариант, где меньше приведенные затраты.

Таким образом, для приведения разновременных затрат в сопоставимый вид используются два метода:

1) дисконтирования затрат к расчетному году;

2) наращивания затрат к расчетному году.

В Методических рекомендациях инвестиционная деятельность рассматривается на определенном промежутке времени в качестве самостоятельного вида деятельности независимо от операционной деятельности. Затем определяется финансовый результат от операционной деятельности по каждому шагу расчета. На завершающем этапе определяется чистый доход путем алгебраического суммирования инвестиционных затрат с финансовыми результатами от операционной деятельности в связи с реализацией инвестиционного проекта.

Теоретически также обоснован и второй метод. Экономически оправданно с целью определения экономического эффекта из общего объема реализованной продукции вычитать сумму текущих затрат (себестоимость за вычетом амортизации) й капитальных вложений. При таком подходе капитальные вложения эквивалентны суммарной величине амортизации за весь срок реализации инвестиционного проекта. Эта задача решается в Методических рекомендациях с помощью метода дисконтирования.

На вопрос, обоснованно ли методологически и методически приводить к расчетному году как единовременные, так и текущие затраты и результаты, большинство западных и отечественных экономистов отвечают утвердительно. Также они утверждают, что нет принципиальной разницы между текущими и единовременными затратами, так как и те, и другие представляют собой рассредоточенные во времени затраты трудовых, материальных, финансовых, энергетических и прочих ресурсов.

Однако величина текущих затрат зависит от объема капитальных вложений, поскольку единовременные затраты направлены на создание более эффективных средств и предметов труда для экономии потребляемых ресурсов.

Капитальные вложения первоначально предназначены для снижения себестоимости, повышения производительности труда, увеличения прибыли.

Рекомендациями предусмотрено для расчетов эффективности инвестиционного проекта использовать следующие показатели: чистый доход (ЧД), чистый дисконтированный доход (ЧДД), внутреннюю норму доходности (ВНД), потребность в дополнительном финансировании (ПФ), индексы доходности затрат и инвестиций, стоимость проекта, капитал риска, срок окупаемости.

5.4.7. Чистый дисконтированный доход

Под дисконтированным доходом понимаются приведенные к настоящей стоимости суммы чистого денежного потока за период эксплуатации инвестиционного проекта.

Дисконтированные величины чистого денежного потока (ДД) отражают текущую, приведенную стоимость ожидаемых в будущем финансовых результатов:

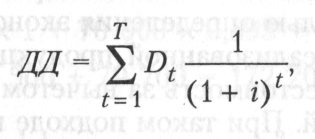
где Dt — чистый денежный поток на t-м шаге расчета, руб.; t — количество интервалов, по которым осуществляется расчет процентных платежей;

i — годовая процентная ставка;

Т — период полезного срока использования проекта.

На ранних стадиях расчета в соответствии с их целями и спецификой финансовые показатели и условия финансовой реализуемости оцениваются в текущих или прогнозных ценах. Остальные показатели определяются в текущих или дефлиро-ванных ценах.

Важнейшим показателем оценки эффективности проекта является чистый дисконтированный доход (ЧДД), или чистая текущая стоимость, — разница между общей суммой дисконтированных денежных потоков за весь срок реализации проекта и первоначальными инвестиционными затратами:

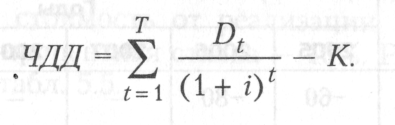
Для признания проекта эффективным необходимо, чтобы ЧДД проекта был положительным; при сравнении альтернативных проектов предпочтение должно отдаваться проекту с большим значением ЧДД.

Очевидно, что при ЧДД > 0 проект следует принять, при ЧДД < 0 проект должен быть отвергнут, при ЧДД = 0 проект не прибылен и не убыточен.

Если проект предполагает последовательное инвестирование финансовых ресурсов в течение нескольких лет, то формула расчета имеет следующий вид: