Тема 5. Потоки платежей. Финансовые ренты

5. 1 Финансовая рента, ее параметры и виды.

Поток платежей –это последовательность платежей в разные моменты времени по операциям, связанным с начислением процентов.

Например, потоком являются поступления (положительные платежи) и выплаты (отрицательные платежи) по вкладам до востребования.

Финансовая рента (аннуитет) – это поток положительных периодических платежей.

Например, рентой являются: взносы в пенсионный и страховой фонды, погасительные платежи потребительского кредита, выплата процентов по облигациям.

Параметры финансовой ренты:

- член ренты - размер платежа;

- период ренты – интервал времени между соседними платежами;

- срок ренты – интервал времени от начала первого до конца последнего периода;

- ставка ренты – ставка, по которой начисляются проценты.

Виды финансовой ренты:

- постоянная рента, если платежи одинаковы, и переменная рента, если платежи различны;

- обычная рента(постнумерандо), если платеж делается в конце периода, и рента

пренумерандо, если платежи делаются в начале периода;

- годовая рента, если один платеж в год, и срочная рента, если несколько платежей за год;

- конечная рента, если ее срок ограничен, и вечная рента, если ее срок не ограничен.

5.2 Обычная рента и ее обобщающие показатели

Обобщающие характеристики финансовой ренты:

- наращенная сумма ренты – это сумма всех платежей вместе с процентами, начисленными на конец ренты.

- современная величина ренты – это сумма всех платежей, дисконтированных на начало ренты.

Наращенная сумма ренты определяется, когда необходимо узнать общий результат накопления в будущем. Современная величина определяется, когда необходимо узнать первоначальную или текущую задолженность на данный момент времени.

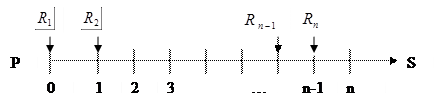
Наиболее распространенной является обычная рента:

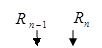			S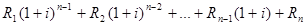

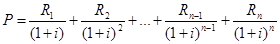
S =

Если рента является постоянной, т.е. 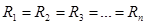, то данные формулы представляют собой суммы членов геометрических прогрессий:

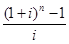- коэффициент наращения ренты, показывает во сколько раз наращенная сумма S больше платежа R;

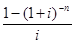-коэффициент приведения ренты, показывает, во сколько раз современная величина Р больше платежа R.

Из формул наращенной суммы S и современной величины P выводят формулы для расчета платежа ренты:

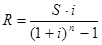
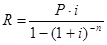
5.3 Финансовые ренты пренумерандо

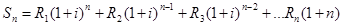
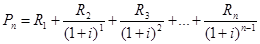
Если сравнить эти формулы с обычной рентой, то можно увидеть следующую взаимосвязь:

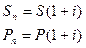
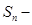наращенная сумма ренты пренумерандо,

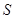- наращенная сумма обычной ренты,

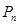-современная величина ренты пренумерандо,

Р -современная величина обычной ренты.

5.4 Вечные финансовые ренты

Определить наращенную сумму вечной ренты невозможно, т.к. не задан срок, на который будут начислены проценты.

Современная величина вечной ренты определяется как предел современной величины постоянной обычной ренты при бесконечно большом сроке:

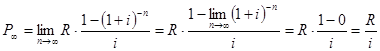
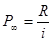, где Р∞ - современная величина вечной ренты,

R - платеж ренты,

i - ставка ренты.

Из формулы современной величины выводят формулы для параметров вечной ренты:

- платеж вечной ренты: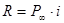

- ставка вечной ренты: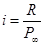

Тема 6 Планирование погашения долга.

6.1 Способы погашения долга

Долг погашается либо единовременным платежом, либо в рассрочку, т.е. несколькими платежами.

При единовременном погашении планирование погашения долга – это расчет наращенной суммы и суммы процентов.

При погашении в рассрочку планирование погашения долга - это расчет следующих показателей:

- срочные уплаты -это периодические расходы, связанные с погашением долга, они возникают, т.к. необходимо периодически погашать очередную часть долга и выплачивать проценты по остатку задолженности;

- обслуживание долга –это общие расходы, связанные с погашением долга (аналог наращенной суммы)

- стоимость долга - это разница между общими расходами и основным долгом (аналог суммы процентов)

Эти показатели рассчитываются по-разному в зависимости от способа погашения:

1)погашение долга единовременным платежом, когда первоначальная сумма долга погашается одним платежом в конце срока, при этом проценты начисляются на сумму основного долга и выплачиваются либо периодически, либо одним платежом вместе с долгом;

2) погашение долга равными долями (равными суммами основного долга), когда первоначальная сумма долга делится на равные доли по количеству выплат. При этом проценты начисляются на остаток задолженности, и выплачивается периодически вместе с долями.

3) погашение долга равными срочными уплатами, когда основной долг с учетом начисленных процентов погашается постоянной обычной рентой.

При планировании погашения долга составляется план погашения в виде следующей таблице:

Период погашения	Остаток задолженности	Проценты	Погашение долга	Срочные уплаты
…
n
Итого:

Если платежи по погашению основного долга известны ( 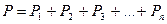), то

- остаток задолженности: ,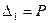

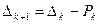
- проценты: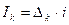

- срочные уплаты: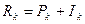

6.2 Погашение долга равными долями.

В этом случае срочные уплаты – это доля долга, плюс проценты, начисленные на остаток задолженности, т.к. остаток задолженности постоянно уменьшается, то соответственно проценты тоже уменьшаются, а значит, уменьшаются и срочные уплаты:

……………………………..

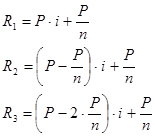
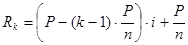, где 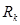- срочные уплаты в период k (k=1,2,3….n),

Р – первоначальная сумма долга,

n - срок долга.

Обслуживание и стоимость долга находят по формулам:

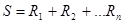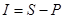, где S - обслуживание долга,

I - стоимость долга.

6.3 Погашение долга равными срочными уплатами.

В этом случае срочные уплаты рассчитываются по формуле платежа постоянной обычной ренты:

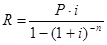
Обслуживание и стоимость долга находят по формулам:

,

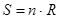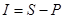
6.4 Потребительский кредит

Существует другой подход к погашению долга равными срочными уплатами, называемый потребительский кредит, когда сразу в момент выдачи кредита определяется его стоимость, т.е. сумма процентов, которая находится, исходя из суммы первоначального долга:

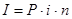
Зная стоимость, рассчитывают общие расходы:

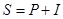
Затем общую сумму расходов делят по количеству выплат и находят срочные уплаты:

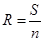
Этот способ является самым несправедливым, т.к. кредит погашается в рассрочку, но при этом проценты начисляются не на остаток задолженности, а на всю сумму долга, то есть получается, что заемщик платит проценты за кредит, которым не пользуется.

Так как ставка, указываемая при потребительском кредите, не отражает реальной доходности операции, то для расчета процентов за текущий период используется правило78, согласно, которому для кредита сроком 1 год с ежемесячным погашением проценты за каждый месяц определяется по схеме:

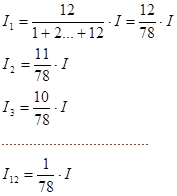
В общем случае эта схема записывается в виде:

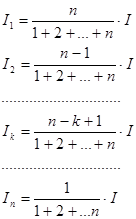
Если погашение долга осуществляется несколько раз в год, то во всех формулах делается следующая корректировка срока и ставки: 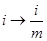, , 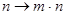где m - количество выплат за год.