Тема 3. ВИЗНАЧЕННЯ ВАРТОСТІ ГРОШЕЙ У ЧАСІ ТА ЇЇ ВИКОРИСТАННЯ У ФІНАНСОВИХ РОЗРАХУНКАХ
Методичні вказівки до вивчення теми
Однією з найважливіших властивостей грошей є їх розподіленість у часі. При аналізі коротких періодів (до 1 року) в умовах стабільної економіки ця властивість незначна і нею часто нехтують. Визначаючи річний обсяг реалізації по підприємству, сумують щомісячну виручку. Аналогічно поступають з усіма іншими грошовими потоками, що дозволяє оперувати їх підсумковими значеннями.
Однак у випадку більш тривалих періодів чи в умовах сильної інфляції виникає серйозна проблема забезпечення порівнянності даних. Та сама номінальна сума грошей, отримана підприємством з інтервалом в один рік і більше, у таких умовах матиме для нього неоднакову цінність. Це зумовлює коригування звітних даних з урахуванням інфляції. Але проблема не зводиться тільки до цього.
Одним з основних принципів фінансового менеджменту є визнання тимчасової цінності грошей, тобто залежності їхньої реальної вартості від величини проміжку часу, що залишається до їхнього одержання чи витрати. В економічній теорії дана властивість називається позитивною тимчасовою перевагою.
Поряд з інфляційним знецінюванням грошей існує ще як мінімум три найважливіші причини даного економічного феномена:
- по-перше, «сьогоднішні» гроші завжди будуть цінніше «завтрашніх» через ризик неотримання останніх, і цей ризик буде тим вище, ніж більше проміжок часу, що відокремлює одержувача грошей від цього «завтра»;
- по-друге, володіючи коштами «сьогодні», економічний суб'єкт може вкласти їх у яке-небудь прибуткове підприємство і отримати прибуток, тоді як одержувач майбутніх грошей позбавлений цієї можливості. Розстаючись із грошима «сьогодні» на певний період часу (припустімо, даючи їх у борг на 1 місяць), власник не тільки піддає себе ризику їхнього неповернення, але й несе реальні економічні втрати у формі не одержаних доходів від інвестування;
- крім того знижується платоспроможність економічного суб’єкта, тому що будь-які зобов'язання, одержувані ним замість грошей, мають більш низьку ліквідність, ніж «живі» гроші. Тобто в кредитора зростає ризик утрати ліквідності, що є третьою причиною позитивної тимчасової переваги.
Різноманітність завдань з визначення зміни вартості грошей у часі можна поєднати наступним чином:
І. Компаундування – визначення майбутньої вартості грошей:
1.1) вкладених одночасно на певний термін під певний процент (просте Компаундування);
1.2) вкладених рівними частками через рівні проміжки часу під певний процентів (FV або S ануїтетів або ренти):
1.2.1) Компаундування звичайної (відстроченої) ренти – це визначення S ренти, вклади по якій проводяться в кінці кожного періоду;
1.2.2) Компаундування вексельної ренти – визначення S ренти, вклади по якій проводяться на початку кожного періоду.
II. Дисконтування – визначення поточної (теперішньої) вартості грошей (англ. РV, Р):
2.1) отриманих в майбутньому одночасно (просте дисконтування);
2.2) отриманих в майбутньому через рівні проміжки часу:
2.2.1) в кінці кожного періоду – це визначення теперішньої вартості звичайних ануїтетів, або Р звичайної (відстроченої) ренти;
2.2.2) на початку кожного періоду – це визначення Р (РV) вексельної ренти.
Надаючи кредит (позики, інвестиції), більшість власників грошей не згодні безкоштовно приймати на себе додаткові ризики і встановлюють відповідні умови його повернення, за яких їм будуть відшкодовані всі моральні й матеріальні незручності.
Кількісною мірою величини цього відшкодування є процентна ставка. З її допомогою може бути визначена як майбутня вартість «сьогоднішніх» грошей (наприклад, якщо їх збираються позичити), так і дійсна (поточна чи приведена) вартість «завтрашніх» грошей (наприклад, тих, якими обіцяють розплатитися через рік після постачання товарів чи надання послуг). У першому випадку говорять про операцію нарощення, тому майбутню вартість грошей часто називають нарощеною. У другому випадку виконується дисконтування чи приведення майбутньої вартості до її поточної величини (на сучасний момент).
Операції нарощення грошей за процентною ставкою більш прості й зрозумілі бо з ними доводиться зустрічатись досить часто, беручи чи даючи гроші в борг. Однак для фінансового менеджменту більш важливе значення має дисконтування грошових потоків, приведення їхньої майбутньої вартості до сучасного моменту часу для забезпечення порівнянності величини розподілених за часом платежів.
Розглянемо деякі елементарні операції з одиничними сумами (разовими платежами).
Процентна (відсоткова) ставка показує ступінь інтенсивності зміни вартості грошей у часі. Абсолютна величина цієї зміни називається відсотком, вимірюється у грошових одиницях (наприклад, грн.) і позначається І. Якщо позначити майбутню суму S, а сучасну (чи первісну) P, то І = S – P. Процентна ставка є відносною величиною, вимірюється в десяткових дробах чи %, і визначається розподілом відсотків на початкову суму:
і = І/Р = (S – P) /Р , (3.1)
Можна помітити, що формула розрахунку процентної ставки тотожна розрахунку статистичного показника «темп приросту». Нарощення початкової суми за процентною ставкою називається декурсивним методом нарахування відсотків.
Крім процентної існує дисконтна ставка d (інша назва – ставка дисконту), величина якої визначається за формулою:
d = D / Р = D / (S – P) / S , (3.2)
де D – сума дисконту.
Порівнюючи формули (3.1) і (3.2), можна помітити, що сума відсотків І і величина дисконту D визначаються як різниця між майбутньою і сучасною вартістю. Однак зміст, вкладений у ці терміни, неоднаковий. Якщо в першому випадку мова йде про приріст поточної вартості, то в другому визначається зниження майбутньої вартості.
Основною областю застосування дисконтної ставки є дисконтування – процес, зворотний нарахуванню відсотків. Але, іноді вона використовується і для нарощення. У цьому разі говорять про антисипативні відсотки.
За допомогою розглянутих вище ставок можуть нараховуватися як прості, так і складні відсотки. При нарахуванні простих відсотків нарощення початкової суми відбувається в арифметичній прогресії, а при нарахуванні складних відсотків – у геометричній.
Операції з простими відсотками.
Нарахування простих декурсивних відсотків визначають за формулою
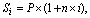(3.3)
а нарахування простих антисипативних відсотків має іншу формулу:
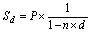, (3.4)
де n – тривалість позички, вимірювана в роках.
Для спрощення обчислень другі співмножники у формулах (3.3) і (3.4) називаються множниками нарощення простих відсотків:
(1 + nі) – множник нарощення декурсивних відсотків;
[1 / (1 - nd)] – множник нарощення антисипативних відсотків.
Нарощення за антисипативним методом завжди відбувається більш швидкими темпами, ніж при використанні процентної ставки. Тому банки використовують цей метод для нарахування відсотків по видаваних ними позичках у періоди високої інфляції. Однак у нього є істотний недолік: як видно з формули (3.4), при n = 1/d знаменник дробу обертається в нуль і вираз втрачає зміст.
Провівши моделювання, одержимо:
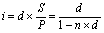. (3.5)
Дотримуючись цієї умови, можна одержувати еквівалентні результати, нараховуючи відсотки як за формулою (3.5), так і за формулою (3.4).
Як правило, процентні ставки встановлюються на рік, тому вони називаються річними. Особливістю простих відсотків є те, що частота процесів нарощення протягом року не впливає на результат. Тобто немає ніякої різниці нараховувати 30% річних 1 раз на рік нарахувати 2 рази по 15% річних. Проста ставка 30% річних при одному нарахуванні в рік називається еквівалентною простій ставці 15% річних при нарахуванні 1 раз в півроку.
Дана властивість характеризує те, що процес нарощення за простою процентною ставкою являє собою арифметичну прогресію з першим членом a1 (а1 = P) і різницею d = (P × і):
____________________________________________________________
*Антисипативним методом нарахування відсотків звичайно користуються в чисто технічних цілях, зокрема, для визначення суми, дисконтування якої по заданим дисконтній ставці і терміном, дасть шуканий результат. Оскільки в практиці суб’єктів господарювання цей метод практично не зустрічається, в подальшому викладі матеріалу він не деталізується.
[P, P + (P × і), P + 2 × (P × і), P + 3 × (P ×і), ..., P + (k - 1) × (P × і)]
Нарощена сума S є ніщо інше як останній k-й член цієї прогресії (S = ak = P + n × P × і), термін позики n дорівнює (k – 1). Тому, якщо збільшити n і одночасно пропорційно зменшити і, то величина кожного члена прогресії, у тому числі й останнього, залишиться незмінною.
Однак тривалість позички (чи іншої фінансової операції, зв'язаної з нарахуванням відсотків) n необов'язково повинна дорівнювати року чи цілому числу років. Прості відсотки найчастіше використовуються при короткострокових (тривалістю менше року) операціях. У цьому разі виникає проблема визначення тривалості позички і тривалості року в днях. Якщо позначити тривалість року в днях буквою K (цей показник називається тимчасовою базою), а кількість днів користування позичкою t, то використане у формулах (3.3) і (3.4) позначення кількості повних років n можна буде виразити як t/K. Підставивши цей вираз в (3.3) і (3.4), для декурсивних відсотків одержимо:
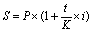, (3.6)
Якщо тимчасова база (K) приймається рівною 365 (366) дням, то відсотки називаються точними. Якщо K = 360 дням, то говорять про комерційні чи звичайні відсотки.
У свою чергу, підрахунок тривалості позички може бути наближеним, коли виходять з тривалості року в 360 днів, або точним – за календарем чи за спеціальною таблицею номерів днів у році. Визначаючи наближену тривалість позички, спочатку підраховують число повних місяців і множать його на 30. Потім додають число днів у неповних місяцях. Загальним для всіх способів підрахунку є правило: день видачі і день повернення кредиту вважаються за один день (назвемо його граничним днем). У наведеному вище умовному прикладі точна тривалість позички складе за календарем 99 днів (21 день у березні + 30 днів у квітні + 31 день у травні + 16 днів у червні + 1 граничний день). Той же результат буде отриманий, якщо використовувати таблицю номерів днів у році (10 березня має порядковий номер 69, а 17 червня – 168). Якщо ж використовувати наближений спосіб підрахунку, то тривалість позички складе 98 днів (21 + 2 × 30 + 16 + 1).
Найбільш часто зустрічаються наступні комбінації тимчасової бази і тривалості позички (цифри в дужках позначають відповідно величину t і K):
1. Точні відсотки з точним числом днів (365/365).
2. Звичайні (комерційні) відсотки з точною тривалістю позички (365/360).
3. Звичайні (комерційні) відсотки з наближеною тривалістю позички (360/360).
Розходження у способах підрахунку днів можуть здаватися несуттєвими, однак при великих сумах операцій і високих процентних ставках вони досягають дуже помітних розмірів.
Зворотним завданням стосовно нарахування відсотків є розрахунок сучасної вартості майбутніх грошових надходжень (платежів) чи дисконтування. У ході дисконтування за відомою майбутньою вартістю S і заданим значенням процентної (облікової) ставки і тривалості операції знаходиться поточна вартість (P). Залежно від того, яка саме ставка (проста процентна чи проста облікова) застосовується для дисконтування, розрізняють два його види: математичне дисконтування і банківський облік.
Види дисконтування
Метод банківського обліку одержав назву від однойменної фінансової операції, в ході якої комерційний банк викуповує у власника (враховує) простий чи перекладний вексель за ціною нижче номіналу до витікання зазначеного на цьому документі терміну погашення. Різниця між номіналом і викупною ціною утворить прибуток банку від цієї операції і називається дисконтом (D). Для визначення розміру викупної ціни (а отже, і суми дисконту) застосовується дисконтування за методом банківського обліку. При цьому використовується проста дисконтна ставка d. Викупна ціна (поточна вартість) векселя визначається за формулою:
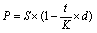, (3.7)
де t – термін, що залишається до погашення векселя, днів.
Другий співмножник цього виразу (1 – (t / k ) × d) називається дисконтним множником банківського обліку по простих відсотках.
Як правило, при банківському обліку застосовують звичайні відсотки з точною тривалістю позички.
Основною областю застосування простих процентної і дисконтної ставок є короткострокові фінансові операції, тривалість яких менше 1 року. Обчислення з використанням простих ставок не враховують можливість реінвестування нарахованих відсотків, тому що нарощення і дисконтування застосовуються щодо незмінної вихідної суми P чи S.
На відміну від них складні ставки відсотків враховують можливість реінвестування відсотків, тому що в цьому випадку застосовується нарощення за формулою не арифметичної, а геометричної прогресії, першим членом якої є початкова сума P, а знаменник дорівнює (1 + і): [P, P × (1 + і), P × (1 + і)2, P × (1 + і)3, ..., P × (1 + і)n ], де n – число років позички, менше числа членів прогресії k на 1 (n = k - 1).
Нарощену вартість (останній член прогресії) знаходять за формулою:
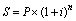, (3.8),
де (1 + і) n – множник нарощення декурсивних складних відсотків.
З позицій фінансового менеджменту використання складних відсотків є більш кращим, тому що визнання можливості власника в будь-який момент інвестувати свої засоби з метою одержання доходу є наріжним каменем усієї фінансової теорії. При використанні простих відсотків ця можливість часто не враховується, тому результати обчислень виходять менш коректними. Проте при короткострокових фінансових операціях, як і раніше, широко застосовуються обчислення простих відсотків.
Найбільш широко складні відсотки застосовують при аналізі довгострокових фінансових операцій (n > 1). На великому проміжку часу повною мірою виявляється ефект реінвестування, нарахування «відсотків на відсотки». У зв'язку з цим питання виміру тривалості операції і тривалості року в днях у випадку складних відсотків стоїть менш гостро. Як правило, неповну кількість років виражають дробовим числом через кількість місяців (3/12 чи 7/12), не вдаючись до більш точних підрахунків днів. Тому у формулі нарахування складних відсотків число років практично завжди позначається буквою n, а не t/K, як це прийнято для простих відсотків. Найбільш педантичні кредитори, приймаючи в увагу велику ефективність простих відсотків на коротких відрізках часу, використовують змішаний порядок нарахування відсотків у випадку, коли термін операції (позички) не дорівнює цілому числу років: складні відсотки нараховуються на період, вимірюваний цілими роками, а відсотки за дробову частину терміну нараховуються за простою процентною ставкою:
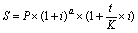, (3.9)
де a – число повних років у складі тривалості операції,
t – число днів у відрізку часу, що приходиться на неповний рік,
K – тимчасова база.
У цьому випадку знову виникає необхідність виконання календарних обчислень за розглянутими вище правилами.
Важливою особливістю складних відсотків є залежність кінцевого результату від кількості нарахувань протягом року. Тут знову позначається вплив реінвестування нарахованих відсотків: база нарахування зростає з кожним новим нарахуванням, а не залишається незмінною, як у випадку простих відсотків. Наприклад, якщо нараховувати 20% річних 1 раз у рік, то початкова сума в 1 тис. грн. зросте під кінець року до 1,2 тис. грн.
(1 × (1+ 0,2)). Якщо ж нараховувати по 10% кожні півроку, то майбутня вартість складе 1,21 тис. грн. (1×(1+0,1) × (1+0,1)), при поквартальному нарахуванні по 5% вона зросте до 1,216 тис. грн. У міру збільшення числа нарахувань (m) і тривалості операції ця різниця буде дуже сильно збільшуватися. Якщо розділити суму нарахованих відсотків при щоквартальному нарощенні на початкову суму, то вийде 21,6% (0,216/1×100), а не 20%. Отже складна ставка 20% при однократному нарощенні і 20% (чотири рази по 5%) при поквартальному нарощенні приводять до різних результатів, тобто вони не є еквівалентними.
Цифра 20% відбиває вже не дійсну (ефективну), а номінальну ставку. Ефективною процентною ставкою є значення 21,6%.
У фінансових розрахунках номінальну складну процентну ставку прийнято позначати буквою j.
Дисконтування по складних відсотках у випадку однократного нарахування відсотків має вигляд:
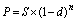, (3.10)
де (1 – d)n – дисконтний множник банківського обліку по складній дисконтній ставці.
Значно більше поширення має математичне дисконтування по складній процентній ставці і. Для m = 1 одержуємо
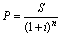, (3.11)
де 1 / (1 + і)n – дисконтний множник математичного дисконтування по складній процентній ставці.
При кількаразовому нарахуванні відсотків протягом року формула математичного дисконтування має вигляд
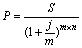, (3.12)
де j – номінальна складна процентна ставка,
1/ (1 + j / m)mn – дисконтний множник математичного дисконтування за складною номінальною процентною ставкою.
В міру збільшення числа нарахувань відсотків протягом року (m) проміжок часу між двома суміжними нарахуваннями зменшується – при m = 1 цей проміжок дорівнює 1 року, а при m = 12 – тільки 1 місяцю. Теоретично можна представити ситуацію, коли нарахування складних відсотків виконується настільки часто, що загальне його число в межах року прагне до нескінченості, тоді величина проміжку між окремими нарахуваннями буде наближатися до нуля, тобто нарахування стане практично постійним. Така на перший погляд гіпотетична ситуація має важливе значення для фінансів і при побудові складних аналітичних моделей (наприклад, при розробці масштабних інвестиційних проектів) часто застосовують безкінечні відсотки. Нескінчена процентна ставка (очевидно, що при постійному нарахуванні мова може йти тільки про складні відсотки) позначається буквою δ (читається «дельта»), часто цей показник називають «сила росту». Формула нарощення за нескінченою процентною ставкою має вигляд
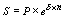, (3.13)
де e – основа натурального логарифма (≈2,71828...),
e δп – множник нарощення нескінчених відсотків.
Для нескінчених відсотків не існує розходжень між процентною і дисконтною ставками – сила росту є універсальним показником. Однак поряд з постійною силою росту може використовуватися перемінна процентна ставка, величина якої міняється за заданим законом (математичною функцією). У цьому випадку можна будувати дуже потужні імітаційні моделі, однак математичний апарат розрахунку таких моделей досить складний і не розглядається в межах нашої теми, так само як і нарахування відсотків за змінною безупинною процентною ставкою.
Безконечне дисконтування з використанням постійної сили росту здійсняється за формулою:
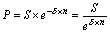, (3.14)
де 1 / e δп – дисконтний множник дисконтування за силою росту.
Між силою росту і дисконтним множником декурсивних відсотків існує наступний зв'язок:
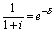. (3.15)
З ускладненням завдань фінансового менеджменту, сфера застосування безкінечних відсотків буде поширюватися, тому що при цьому стає можливим використання більш потужного математичного апарату. Особливо наочно це виявляється у випадку безкінечних процентних ставок
Визначення поточної і майбутньої величини грошових потоків
Основні правила процентних обчислень залишаються незмінними і для сукупності (потоку) платежів, однак виникає необхідність ввести кілька додаткових понять. У фінансовому аналізі для позначення грошових потоків у найбільш загальному змісті використовується термін рента. Кожен окремий рентний платіж називають членом ренти.
Окремим випадком ренти є фінансова рента, або аннуїтет – такий потік платежів, усі члени якого рівні один одному, як і інтервали часу між ними. Форму ануїтетів мають багато фінансових потоків, наприклад, виплата доходів по облігаціях чи платежі по кредиту, страхові внески та ін.
Принцип непостійної цінності грошей унеможливлює пряме підсумовування членів ренти. Для врахування впливу фактора часу до кожного члена ренти застосовують правила нарощення і дисконтування. Причому в аналізі грошових потоків застосовується техніка обчислення тільки складних відсотків, тобто передбачається, що одержувач потоку має змогу реінвестувати одержувані ним суми. Якби розміри рент завжди обмежувалися двома-трьома членами, то необхідність створення спеціальних способів розрахунку грошових потоків, можливо, і не виникла б. Ні в теорії, ні на практиці таких обмежень немає, навпаки, існують великі, дуже великі і навіть нескінченні грошові потоки (вічні ренти).
Існують спеціальні методи, що дозволяють аналізувати ренту не по кожному її члену окремо, а як єдину сукупність визначати розміри інших важливих параметрів ренти.
Залежно від числа платежів за період розрізняють річні й p-термінові ренти. У першому випадку за один період ренти (рівний, як правило, одному року) робиться 1 виплата; у другому протягом періоду робиться p виплат
(p > 1). У випадку дуже частих виплат рента може розглядатися як нескінченна (p → ∞). Частіше у фінансовому аналізі мають справу з дискретними рентами, для яких p – кінцеве ціле число. Так само, як і при використанні складної процентної ставки, для одиничних сум, нарощення (дисконтування) рент може робитись 1 раз за період, m раз за період чи постійно. За величиною членів грошового потоку ренти можуть бути постійними (з рівними членами) і змінними. За імовірності виплат ренти поділяються на реальні й умовні. У випадку умовної ренти виплата її членів ставиться в залежність від настання якої-небудь умови. За своєю загальною тривалістю (чи за числом членів) розрізняють обмежені (з кінцевим числом членів) і нескінченні (вічні, безстрокові) ренти. Щодо фіксованого моменту початку виплат ренти можуть бути негайними і відкладеними (відстроченими). Ренти, платежі по яких робляться наприкінці періоду, називаються звичайними чи постнумерандо; при виплатах на початку періоду говорять про ренти пренумерандо.
Розглянемо приклад визначення майбутньої величини обмеженої постійної ренти (ануїтета) постнумерандо, яка виплачується 1 раз за рік
(p = 1), відсотки нараховуються за складною ефективною процентною ставкою і 20% річних нараховуються також 1 раз за рік (m = 1). Розмір річного платежу R складає 3 тис. грн., загальний термін ренти n дорівнює 5 років.
Таблиця 3.1
Нарощення грошового потоку
| № періоду | Всього | |||||
| 1. Член ренти, тис.грн. | ||||||
| 2. Час до кінця ренти, періодів (років) | – | |||||
| 3. Множник нарощення | (1+0,2)4 | (1+0,2)3 | (1+0,2)2 | (1+0,2)1 | (1+0,2)0 | – |
| 4. Нарощена величина, тис. грн. (р.1×р.3) | 6,22 | 5,18 | 4,32 | 3,6 | 22,32 |
Отримане значення (22,32 тис. грн.) очевидно, більше арифметичної суми окремих членів ренти (15 тис. грн.), але вона значно менше тієї очікуваної суми, що могла бути отримана, якби проводилось нарощування за ставкою 20% всі 15 тис. грн. за весь термін ренти. Нарощена сума ренти S отримана шляхом послідовного нарахування відсотків за кожним членом ренти і наступного сумування одержаних результатів.
Увівши позначення k = номера періоду ренти, в найбільш загальній формі даний процес можна виразити наступною формулою:
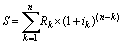. (3.16)
У нашому прикладі член ренти R незмінний протягом усього терміну, процентна ставка і також постійна. Тому нарощену величину ренти можна знайти як суму геометричної прогресії з першим членом 3000 і знаменником (1 + 0,2):
.
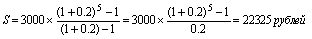Отже, від загальної формули нарощення ренти можна перейти до формули нарощення ануїтета:
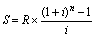. (3.17)
Другий співмножник цього виразу – [((1+і)n - 1) / і] називається множником нарощення ануїтету. Так само як і у випадку з нарахуванням відсотків на одиничні суми, значення таких множників табульовані, що дозволяє полегшити відсоткові нарахування грошових потоків.
Нарощення грошових потоків має місце при періодичному внесенні на банківський депозит фіксованих сум з метою акумулювання коштів до певного моменту часу. Наприклад, розмістивши довгострокову облігаційну позику, підприємство готується до погашення суми основного боргу наприкінці терміну позики шляхом періодичного внесення на банківський рахунок фіксованих платежів під установлений відсоток. У такий спосіб до моменту погашення облігаційної позики підприємство сконцентрує достатні кошти. Аналогічні завдання вирішуються в ході формування пенсійного фонду чи при акумулюванні суми для оплати навчання дітей. Наприклад, піклуючись про свою старість, людина може поряд з обов'язковими відрахуваннями в державний Пенсійний фонд вносити частину свого щомісячного заробітку на банківський депозит під відсотки. Нарощення суми такого внеску буде відбуватися за описаним вище алгоритмом. Таким же шляхом підприємства можуть формувати амортизаційний фонд для планової заміни устаткування.
Зворотний щодо нарощення процес – дисконтування грошового потоку, дуже важливий для фінансового менеджменту, бо в результаті визначаються показники – критерії прийняття фінансових рішень.
Розглянемо цей процес більш докладніше. Припустимо, що розглянутий у нашому прикладі грошовий потік характеризує плановані надходження від реалізації інвестиційного проекту. Доходи повинні надходити наприкінці періоду. Оскільки ці надходження планується одержати в майбутньому, а інвестиції, необхідні для виконання проекту, повинні бути зроблені вже сьогодні, підприємству необхідно зіставити величину майбутніх доходів із поточною величиною витрат. Для забезпечення порівнянності даних величина майбутніх надходжень повинна бути приведена до дійсного моменту, іншими словами даний грошовий потік повинен бути дисконтовано за ставкою 20%. Підприємство зможе визначити сьогоднішню вартість майбутніх доходів. При цьому процентна ставка буде виступати як вимірник альтернативної вартості цих доходів: вона показує, скільки грошей могло б одержати підприємство, якби розмістило приведену (сьогоднішню) вартість майбутніх надходжень на банківський депозит під 20%.
Операції нарощення і дисконтування грошових потоків взаємооборотні, тобто нарощена сума ренти може бути отримана нарахуванням відсотків за відповідною складною ставкою і на сучасну (приведену) величину цієї ж ренти (S = PV× (1+і)n).
Таблиця 3.2
Дисконтування грошового потоку
| № періоду | разом | |||||
| 1. Член ренти, тис. грн. | ||||||
| 2. Число років від початкової дати | ||||||
| 3. Множник дисконтування | 1/(1+0,2)1 | 1/(1+0,2)2 | 1/(1+0,2)3 | 1/(1+0,2)4 | 1/(1+0,2)5 | – |
| 4. Приведена величина, тис. грн. (р.1× р.3) | 2,5 | 2,08 | 1,74 | 1,45 | 1,21 | 8,98 |
З табл. 3.2 видно, що при альтернативних витратах 20% сьогоднішня вартість майбутніх доходів складає 8,98 тис. грн. Саме ця величина і повинна порівнюватися з інвестиціями для визначення доцільності прийняття проекту чи відмови від його реалізації. Узагальнюючи алгоритм, за яким виконувалися розрахунки, одержуємо загальну формулу дисконтування грошових потоків:
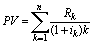. (3.18)
Тому що в нашому прикладі й і R – постійні величини, знову застосовуючи правило підсумовування геометричної прогресії, одержимо формулу дисконтування ануїтету:
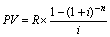. (3.19)
Другий співмножник цього виразу (1 - (1 + і)-n) / і називається дисконтним множником ануїтету.
Формули (3.18) і (3.19) описують найбільш загальні випадки нарощення і дисконтування ануїтетів: розглядаються тільки обмежені ренти, виплати і нарахування відсотків виконуються 1 раз протягом року, використовується тільки ефективна відсоткова ставка і. Так само як і у випадку одиничних сум, усі ці параметри можуть мінятися. Тому існують модифіковані формули нарощення і дисконтування ануїтетів, що враховують особливості окремих грошових потоків. Основні з них, що відносяться до обмежених грошових потоків, представлені в табл. 3.3.
У табл. 3.3 не знайшли відображення формули розрахунку необмежених грошових потоків, тобто вічних рент чи перпетуїтетів.
Таблиця 3.3
Основні формули нарощення і дисконтування обмежених ануїтетів
| Види рент | Нарощення | Дисконтування |
| 1. Річна з нарахуванням кілька разів у році (p = 1, m > 1) |  |  |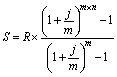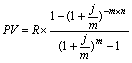
| 2. p-термінова з нарахуванням 1 раз у році (p > 1, m = 1) |  |  |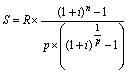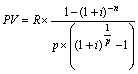
| 3. p- термінова з нарахуванням кілька разів у році (p > 1, m > 1, p = m) |  |  |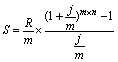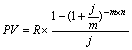
| 4. p- - термінова з нарахуванням кілька разів у році (p > 1, m > 1, p ≠ m) |  |  |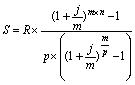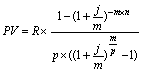
| 5. Річна з нарахуванням безупинних відсотків (p = 1, d) |  |  |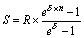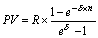
| 6. p- термінова з нарахуванням безупинних відсотків (p > 1, d) |  |  |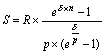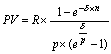
Очевидно, що майбутню вартість ренти такого роду визначити неможливо – її сума також буде прагнути до нескінченності, однак приведена величина вічного грошового потоку може бути виражена дійсним числом. Формула її визначення дуже проста:
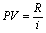, (3.20)
де R – член ренти (разовий платіж);
i – складна процентна ставка.
Якщо необмежена рента виплачується p раз у році, і нарахування відсотків по ній проводиться m раз за рік, причому m = p, то формула розрахунку її приведеної вартості має вигляд:
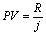, (3.21)
де j – номінальна процентна ставка.
У випадку, якщо член вічної ренти R щорічно збільшується з постійним темпом приросту g, те приведена вартість такої ренти визначається за формулою:
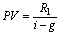, (3.22)
де R1 – член ренти в першому році.
Дана формула має рацію при g < і. Вона застосовується в оцінці звичайних акцій.
Обчислення основних параметрів грошових потоків
Зіставлення різних варіантів погашення позики тільки за критерієм загальної величини виплачених відсотків, не зовсім коректне: порівнюються різні грошові потоки, для яких крім абсолютних сум має значення, в якому конкретно періоді часу гроші були сплачені чи отримані.
Розглянемо докладніше, що собою являє представляє кожний з цих потоків (табл. 3.4).
Таблиця 3.4
Порівняння варіантів виплати позики
| Члени потоку | Варіанти погашення позики, тис. грн | ||
| повернення основного боргу в кінці строку | фіксована виплата основного боргу | фіксована термінова сплата | |
| 1. Одержання позики | +6000 | +6000 | +6000 |
| 2. Платіж наприкінці 1 року | -1200 | -3200 | -2848,4 |
| 3. Платіж наприкінці 2 року | -1440 | -2800 | -2848,4 |
| 4. Платіж наприкінці 3 року | -7728 | -2400 | -2848,4 |
| 5. Приведена до моменту одержання позики сума виплат | -6472,2 | -6000 | -6000 |
Унаслідок дії принципу тимчасової цінності грошей додавання членів цих потоків є безглуздою операцією – платежі, зроблені з інтервалом в 1 рік, не порівнянні. Тому в рядку 5 табл. 3.4 розрахована дисконтована за ставкою 20% величина кожного з потоків (в останній графі цієї таблиці представлений ануїтет). Два інших потоки складаються з нерівних членів, їх дисконтування виконано за загальною формулою. Як видно з результатів розрахунків, найбільшу негативну величину (- 6472,2) має приведена сума платежів по першому потоці, вона навіть перевищує суму отриманої позики. Тобто, погашаючи борг на таких умовах, підприємство реально несе фінансові втрати. Два останніх варіанти не погіршують фінансового стану підприємства.
Порівнюючи між собою приведені величини грошових притоків і відтоків фінансової операції, визначають найважливіший фінансовий показник – чисту приведену вартість (NPV). Найбільш загальна формула визначення цього показника є такою:
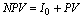, (3.23)
де I0 – початкові інвестиції в проект (відтік грошей),
PV – приведена вартість майбутніх грошових потоків за проектом.
При використанні цієї формули всі грошові доходи позначаються позитивними цифрами, а відтоки коштів (інвестиції, витрати) – негативними.
У нашому прикладі підприємство одержувало кошти (сума позики 6 млн. грн), а потім протягом 3 років проводило грошові витрати, тобто мали місце відтоки коштів. Тому до початкового моменту приводилися не надходження, а витрати. Звичайно при реалізації інвестиційних проектів спостерігається зворотна картина: спочатку підприємство вкладає кошти, а потім одержує періодичні доходи від цих вкладень. Тому визначимо NPV (3.23) з урахуванням правил дисконтування грошових потоків:
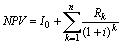, (3.24)
де n – загальний термін фінансової операції (проекту);
Rk – елемент дисконтованого грошового потоку (член ренти) в періоді k;
k – номер періоду.
Під процентною ставкою і (у даному випадку її називають ставкою порівняння) розуміється річна складна ефективна ставка декурсивних відсотків. Термін операції n у загальному випадку вимірюється роками. Якщо ж реальна операція не відповідає цим умовам, тобто інтервали між платежами не рівні року, то як одиницю виміру терміну приймаються частки року, вимірювані, як правило, у місяцях, поділених на 12. Наприклад, інвестиції в сумі 500 тис. грн принесуть у перший місяць 200 тис. грн додаткового доходу, в другий 300 тис. грн і в третій – 700 тис. грн. Ставка порівняння дорівнює 25%. Чиста приведена вартість даного проекту складе 1 млн. 147 тис. грн:
.
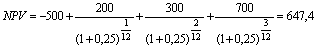Досить розповсюдженою є помилка, коли в подібних випадках намагаються розрахувати місячну процентну ставку розподілом річної ставки на 12, а термін проекту вимірюють у цілих місяцях (замість 1/12 року беруть 1 місяць, замість 2/12 – 2 місяці і т.д.). У цьому разі буде отриманий неправильний результат, тому що виникне ефект щомісячного реінвестування нарахованих складних відсотків.
Якщо грошовий потік складається з однакових і рівномірно розподілених виплат (тобто являє собою ануїтет), можна спростити розрахунок NPV, скориставшись формулами дисконтування ануїтетів. Наприклад, якби в проекті було передбачене одержання протягом трьох місяців по 400 тис. грн доходу щомісяця (тобто R = 4800), то треба розрахувати приведену вартість ануїтета терміном 3/12 року і числом виплат p = 3. Застосувавши формулу (табл. 3.3), одержимо
.
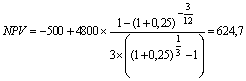Крім правильного обчислення чистої приведеної вартості, необхідно розуміти її фінансовий зміст. Позитивне значення цього показника вказує на фінансову доцільність здійснення операції чи реалізації проекту.
Негативна NPV свідчить про збитковість інвестування. У прикладі з проектом отримане позитивне значення NPV, що свідчить про його інвестиційну привабливість.
Другим важливим фінансовим показником є внутрішня норма прибутковості (ІRR). ІRR – це така річна процентна ставка, що робить NPV проекту рівним нулю, тобто коли поточна вартість грошових надходжень проекту дорівнює величині інвестицій.
Визначення ІRR не має прямого алгебраїчного рішення, тому знайти її величину можна шляхом підбору значення або використовуючи який-небудь ітераційний спосіб. Трудомісткість цієї проблеми практично знімається наявністю ПК з пакетом електронних таблиць.
Питання до теми
1. Необхідність і сутність визначення часової вартості грошей. Основні причини зміни вартості грошей у часі.
2. Типи задач при визначенні вартості грошей у часі. Класифікація, алгоритм і способи їх вирішення.
3. Проблеми застосування принципів Компаундування та дисконтування в Україні. Значення встановлення зміни часової вартості грошей у світовому господарстві.
4. Поняття і сутність Компаундування. Просте Компаундування. Компаундування ануїтетів (ренти). Поняття звичайної і вексельної ренти.
5. Поняття і сутність дисконтування. Просте дисконтування. Дисконтування звичайної і вексельної ренти.
6. Оцінка майбутньої і теперішньої вартості грошей з урахуванням фактора інфляції.
7. Як вигідніше вкладати гроші: водночас чи рівним частками через рівні проміжки часу?
Література
1. Бланк И.А. Финансовый менеджмент. – К.: Ника-Центр, 2004. – С. 68-86.
2. Брігхем Є.Г. Основи фінансового менеджменту. – К.: Молодь, 1997. – С. 251-297.
3. Финансовый менеджмент: теория и практика: Учебник/ Под ред. Е.С. Стояновой – М.: Изд-во «Перспектива», 2004. – с.84-132
4. Фінансовий менеджмент.: Навч.посібник/За ред. Поддерьогіна А.М. – К.: КНЕУ, 2001. – с. 99-128
5. Фінансовий менеджмент.: Навч.посібник/За ред. Г.Г. Кірейцева – К.: КНЕУ, 2002. – с. 111-144