Методика выполнения задания. 1. Построение точечного графика экспериментальных данных – это наиболее простой и наглядный способ определения формы и направления связи в случае парной

1. Построение точечного графика экспериментальных данных – это наиболее простой и наглядный способ определения формы и направления связи в случае парной корреляции (рис.10).

Для построения графика надо выделить столбцы Среднегодовой удой и Расход кормов из таблицы 1, выбрать Вставка-Диаграмма – Точечная. Необходимо учесть, что первый столбец Excel автоматически принимает за x, а второй за y, для упрощения процедуры построения столбцы лучше поменять местами.

Рисунок 10 Зависимость продуктивности коров от уровня кормления

Анализируя полученный график, легко заметить, что прослеживается прямая линейная зависимость между уровнем кормления коров и их молочной продуктивностью, что и было установлено в результате проведенной аналитической группировки в задании 1.

2. Оценка тесноты связи между признаками осуществляется с помощью линейного коэффициента корреляции (r), который изменяется в пределах от -1 до 1. Чем ближе коэффициент корреляции по модулю к единице, тем сильнее связь между признаками.

Для расчета коэффициента корреляции необходимо использовать функцию КОРРЕЛ(), в качестве аргумента которой используются ссылки на столбцы Расход кормов и Среднегодовой удой (порядок указания столбцов не имеет значения).

В рассматриваемом примере r=0.879, что свидетельствует о наличии сильной связи, положительный знак коэффициента указывает на то, что связь между параметрами прямая.

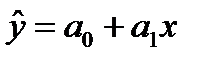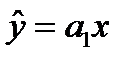3. Линейная зависимость может выражаться уравнением прямой линии: или , где 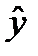- продуктивность коров (результативный признак); 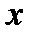- расход кормов на 1 голову (факторный признак); 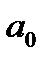, 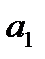- параметры уравнения, которые имеют вполне конкретный смысл: 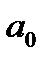-это величина среднегодового удоя в случае, если расход кормов (х) будет равен 0 ц.к.ед., 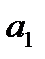- показывает, на сколько ц. изменится среднегодовой удой от коровы при изменении расхода кормов на 1 ц.к.ед.

В каждом конкретном случае необходимо решать, какая из линейных моделей подходит для описания анализируемой предметной области.

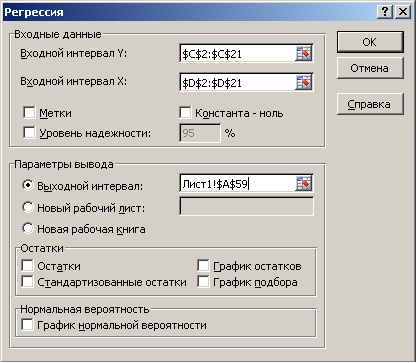
ссылка на столбец содержащий расход кормов на корову, ц.к.ед. ссылка на столбец, содержащий среднегодовой удой от одной коровы, ц. отмечается в случае получения модели без свободного члена ссылка на область размещения результатов расчета Нахождение коэффициентов регрессии осуществляется с помощью пункта меню Сервис – Анализ данных – Регрессия (рис.11). Рисунок 11 Диалоговое окно регрессии

Результаты решения выводятся на экран в виде, представленном на рис. 12.

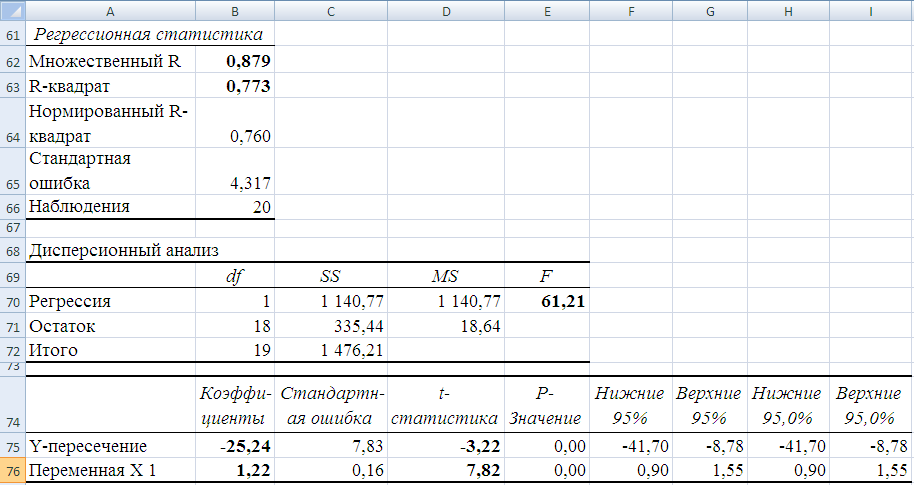
Рисунок 12 Результаты корреляционно-регрессионного анализа

В таблице 14 представлено соответствие показателей, рассчитанных с помощью ТП Excel с общепринятой терминологией.

Таблица 14 Соответствие расчетных показателей с общепринятой терминологией

Адрес ячейки	Обозначение показателя	Наименование показателя в общепринятой терминологии
B62	r	Коэффициент корреляции
B63		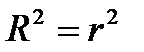Коэффициент детерминации
E70		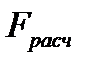Расчетное значение критерия Фишера
B75		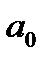Свободный член в регрессионной модели
B76		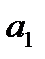Коэффициент модели, стоящий перед переменной x
D75		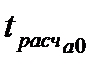Расчетное значение критерия Стьюдента для параметра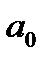
D76		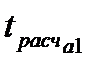Расчетное значение критерия Стьюдента для параметра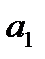

Таким образом, в ходе вычислений получили регрессионную модель следующего вида: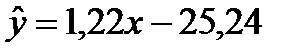

4. Проверка полученной модели на адекватность осуществляется в несколько этапов:

Ый этап

Адекватность модели по критерию Фишера осуществляется по следующему условию: модель адекватна если .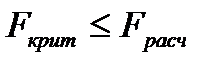

Критическое значение Фишера определяется по формуле FРАСПОБР(α;k1;k2), где α=0,05 (допустимая погрешность модели), k1=1 (число факторных признаков в модели), k2=m-(k1+1)= 20-(1+1)=18 (m - число экспериментальных данных).

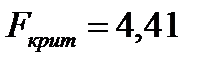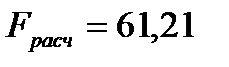, , следовательно, построенная модель по критерию Фишера адекватна.

Ой этап

Значимость коэффициентов модели по критерию Стьюдента осуществляется по следующему условию: коэффициент значим, если .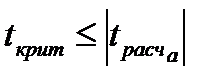

Критическое значение Стьюдента определяется по формуле: СТЬЮДРАСПОБР(α;k), где α=0,05 (допустимая погрешность модели), k=m-n=20-2=18 (m - число экспериментальных данных, n – число коэффициентов регрессии в модели ( , )).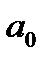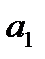

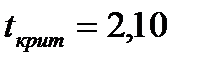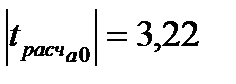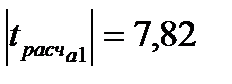, , , таким образом, критическое значение критерия Стьюдента ни по одному коэффициенту не превышает расчетных значений, можно сделать вывод о значимости коэффициентов , .

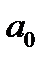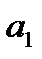Если окажется незначим коэффициент 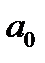, то необходимо построить модель без свободного члена, в случае незначимости коэффициента 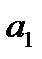делается вывод о том, что факторный признак выбран не верно[4].

Ий этап

Оценка качества модели по средней ошибке аппроксимации, проводится по следующей формуле:

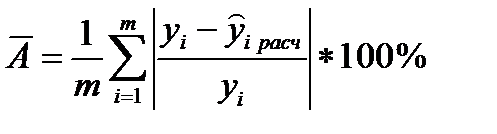
где 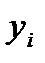фактическое значение результативного признака, 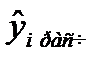- значение результативного признака, рассчитанного по полученной модели, m – число наблюдений.

Средняя ошибка аппроксимации показывает среднее отклонение расчетных значений от экспериментальных. Если 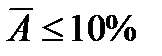, то качество модели считается хорошим, если 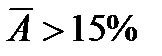, то делается вывод о неудовлетворительном качестве полученной модели.

	Определение средней ошибки аппроксимации с использованием табличного процессора представлено на рис. 13.
Рисунок 13 Расчет средней ошибки аппроксимации в ТП Excel

В результате проведенных расчетов 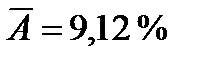, что говорит о хорошем качестве полученной модели.

5. Полученную модель 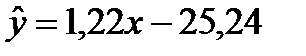можно использовать для прогнозирования среднегодового удоя на одну корову (ц) при заданном расходе кормов на голову (ц.к.ед.).

Так, если расход кормов на одну голову составит 50 ц.к.ед., то среднегодовой удой от коровы составит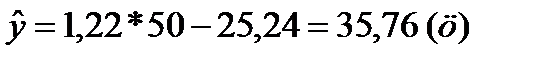

6. Коэффициент эластичности определяется по формул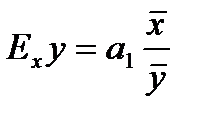е , где 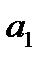- коэффициент регрессионного уравнения, 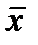-среднее значение факторного признака по всей совокупности, 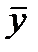- среднее значение результативного признака по всей совокупности.

В рассматриваемом примере 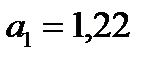, среднее значение расхода кормов на одну корову (ц.к.ед.) и среднегодовой надой молока на корову (ц) рассчитаны в таблице 4 и равны 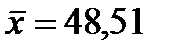, 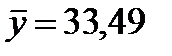. Коэффициент эластичности определяется следующим выражением: 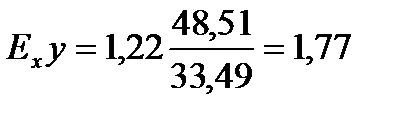. Данное значение свидетельствует о том, что если расход кормов (ц.к.ед.) на одну голову увеличить на 1 %, это приведет к росту среднегодового надоя на корову (ц) на 1,77 %.