Классическое определение вероятности.
Как было сказано выше, при большом числе n испытаний частота P*(A)=m/n появления события A обладает устойчивостью и дает приближенное значение вероятности события A, т.е. 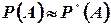 .
.
Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. Ведь нам нужно заранее знать вероятность некоторого события, еще до опыта. В этом и состоит эвристическая, предсказательная роль науки. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности).
Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.
Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события.
Рассмотрим другой пример. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).
События 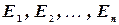 в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них. Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6.
в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них. Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6.
Очевидно, любое событие A и противоположное ему событие  образуют полную группу.
образуют полную группу.
Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A. Так, если A— появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A.
Пусть события 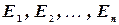 в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют
в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют 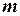 исходов испытания. Тогда вероятностью события A в данном опыте называют отношение
исходов испытания. Тогда вероятностью события A в данном опыте называют отношение 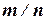 . Итак, мы приходим к следующему определению.
. Итак, мы приходим к следующему определению.
Вероятностью P(A) события в данном опыте называется отношение числа 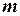 исходов опыта, благоприятствующих событию A, к общему числу
исходов опыта, благоприятствующих событию A, к общему числу 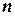 возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:
возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий: 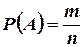 .
.
Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности.
Пример 1.1. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным.
Решение: Число стандартных подшипников равно 1000—30=970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из 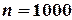 равновероятных исходов, из которых событию A благоприятствуют
равновероятных исходов, из которых событию A благоприятствуют 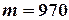 исходов. Поэтому
исходов. Поэтому 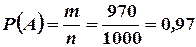 .
.
Пример 1.2. В урне 10шаров: 3 белых и 7 черных. Из урны вынимают сразу два шара. Какова вероятность р того, что оба шара окажутся белыми?
Решение: Число 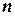 всех равновероятных исходов испытания равно числу способов, которыми можно из 10 шаров вынуть два, т. е. числу сочетаний из 10 элементов по 2 (полная группа событий):
всех равновероятных исходов испытания равно числу способов, которыми можно из 10 шаров вынуть два, т. е. числу сочетаний из 10 элементов по 2 (полная группа событий):
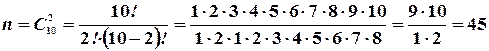 .
.
Число благоприятствующих исходов (сколькими способами можно из 3 шаров выбрать 2): 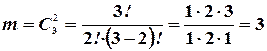 . Следовательно, искомая вероятность
. Следовательно, искомая вероятность 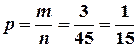 .
.
Забегая вперед, эту задачу можно решить и другим способом.
Решение: Вероятность того, что при первом испытании (вытаскивании шара) будет вынут белый шар, равна 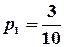 (всего шаров 10, из них 3 белых). Вероятность того, что при втором испытании будет вынут снова белый шар равна
(всего шаров 10, из них 3 белых). Вероятность того, что при втором испытании будет вынут снова белый шар равна 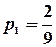 (всего шаров стало 9, т.к. один вынули, белых стало 2, т.к. вынули именно белый). Следовательно, вероятность совмещения событий равна произведению их вероятностей, т.е.
(всего шаров стало 9, т.к. один вынули, белых стало 2, т.к. вынули именно белый). Следовательно, вероятность совмещения событий равна произведению их вероятностей, т.е. 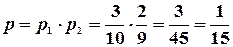 .
.
Пример 1.3. В урне 2 зеленых, 7 красных, 5 коричневых и 10 белых шаров. Какова вероятность появления цветного шара?
Решение: Находим соответственно вероятности появления зеленого, красного и коричневого шаров: 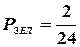 ;
; 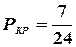 ;
; 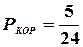 . Так как рассматриваемые события, очевидно, несовместны, то, применяя аксиому сложения, найдем вероятность появления цветного шара:
. Так как рассматриваемые события, очевидно, несовместны, то, применяя аксиому сложения, найдем вероятность появления цветного шара:
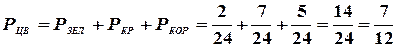 .
.
Либо, другим способом. Вероятность появления белого шара равна 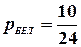 . Тогда вероятность появления небелого шара (т.е. цветного), т.е. вероятность противоположного события, равна
. Тогда вероятность появления небелого шара (т.е. цветного), т.е. вероятность противоположного события, равна 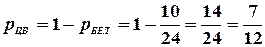 .
.
Геометрическое определение вероятности. Чтобы преодолеть недостаток классического определения вероятности (оно неприменимо к испытаниям с бесконечным числом исходов), вводят геометрические определение вероятности - вероятности попадания точки в область (отрезок, часть плоскости и т. д.).
Пусть отрезок 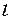 составляет часть отрезка
составляет часть отрезка 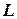 . На отрезке
. На отрезке 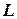 наудачу поставлена точка, что означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка
наудачу поставлена точка, что означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка 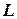 , вероятность попадания точки на отрезок
, вероятность попадания точки на отрезок 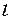 пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка
пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка 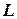 . В этих предположениях вероятность попадания точки на отрезок
. В этих предположениях вероятность попадания точки на отрезок 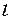 определяется равенством
определяется равенством
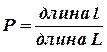 . (1.4)
. (1.4)
Далее, пусть плоская фигура 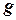 составляет часть плоской фигуры
составляет часть плоской фигуры 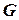 . На фигуру
. На фигуру 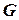 наудачу брошена точка, что означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры
наудачу брошена точка, что означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры 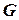 , вероятность попадания брошенной точки на фигуру
, вероятность попадания брошенной точки на фигуру 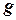 пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно
пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно 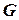 , ни от формы
, ни от формы 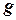 . В этих предположениях вероятность попадания точки в фигуру
. В этих предположениях вероятность попадания точки в фигуру 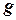 определяется равенством
определяется равенством
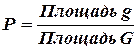 . (1.4a)
. (1.4a)
Замечание: в случае классического определения вероятность достоверного (невозможного) события равна единице (нулю); справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае же геометрического определения вероятности обратные утверждения не имеют места.
