Проверка нормальности закона распределения

	Y1	X1	Z1
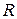	4,5	12,3
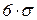	7,3641	5,6983	32,3382
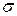	1,2274	0,9497	5,3897
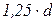	1,3467	1,1100	5,5333

Основные соотношения между абсолютными показателями вариации для признака Y1 не выполняются, поэтому распределение совокупности по признаку Y1 не отвечает нормальному закону.

Основные соотношения между абсолютными показателями вариации для признака X1 не выполняются, поэтому распределение совокупности по признаку X1 не отвечает нормальному закону.

Основные соотношения между абсолютными показателями вариации для признака Z1 не выполняются, поэтому распределение совокупности по этому признаку не отвечает нормальному закону

2. Относительные показатели вариации признаков:

Коэффициент осцилляции - рассчитывается как отношение размаха вариации к среднему значению признака, то есть:

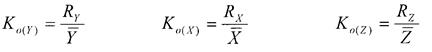
Линейный коэффициент вариации – рассчитывается как отношение среднего линейного отклонения к среднему значению признака, то есть:

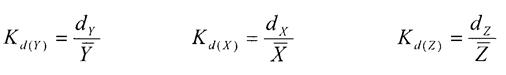
Квадратичный коэффициент вариации – рассчитывается как отношение среднего квадратичного отклонения к среднему значению признака, то есть:

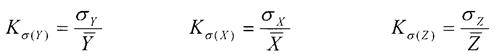
Коэффициент асимметрии - рассчитывается как отношение разницы между средним значением признака и модой к среднему квадратичному отклонению признака, то есть:

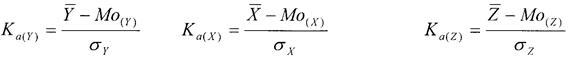
Модальные значения признаков находим с помощью функции «=МОДА(массив)».

Занесем полученные результаты расчетов к общей таблице показателей вариации:

Таблица 6

Относительные показатели вариации признаков

	Y1	X1	Z1
Коэффициент осцилляции	0,1605	0,8961	0,8744
Линейный коэффициент вариации	0,0384	0,0647	0,0744
Квадратичный коэффициент вариации	0,0438	0,0692	0,0906
Ассиметрия	6,2859	-0,9196	0,6432

Выводы:

Таким образом, на основе анализа коэффициентов вариации видно, что наиболее вариационным является признак Z1 – заемные средства.

Также, по численной характеристике коэффициентов асимметрии можно сделать вывод:

• о существенной левосторонней асимметрии признака Y1.

• о умеренной правосторонней асимметрии признака X1.

• о умеренной левосторонней асимметрии признака Z1.

Использованная литература

1. Гмурман В.Е. Введение в теорию вероятностей и математическую статистику. – М.: Высшая школа, 1966.

2. Головач А.В. Статистика. Учебное пособие. – К.: Высшая школа, 1990.

3. Мешалкин Л.Д. Сборник задач по статистике. – М.: Изд. МГУ, 1996.

4. Статистика підприємництва: Підручник / Вашків В.П., Пастер П.І., Сторожук В.П., Ткач Є.І. – К.: Слобожанщина, 1999. – 600 с.

5. Яблочник А.Л. Общая теория статистики: Для программированного обучения. Учебное пособие. – М.: Финансы и статистика, 1993.