Использование специальных функций

В мастере функций Ехсеl имеется ряд специальных функций, предназначенных для вычисления выборочных характеристик. Прежде всего, это функции, характеризующие центр распределения.

- Функция СРЗНАЧ вычисляет среднее арифметическое из нескольких массивов (аргументов) чисел. Аргументы число1, число2, ... — это от 1 до 30 массивов, для которых вычисляется среднее. Например, если ячейки А1:А7 содержат числа 10, 14, 5, 6, 10, 12 и 13, то средним арифметическим СРЗНАЧ(A1:А7)является 10

- Функция СРГАРМ позволяет получить среднее гармоническое множества данных. Среднее гармоническое — это величина, обратная к среднему арифметическому обратных величин. Например, СРГАРМ(10;14;5;6;10;12;13) равняется 8,768.

- Функция МЕДИАНА позволяет получать медиану заданной выборки. Медиана — это элемент выборки, число элементов выборки со значениями больше которого и меньше которого равно. Например, МЕДИАНА(10;14;5;6;10;12;13) равняется 10.

- Функция МОДА вычисляет наиболее часто встречающееся значение в выборке. Например, МОДА(10;14;5;6;10;12;13) равняется 10.

К специальным функциям, вычисляющим выборочные характеристики, характеризующие рассеяние вариант, относятся ДИСП, СТАНДОТКЛОН, ПЕРСЕНТИЛЬ.

- функция ДИСП позволяет оценить дисперсию по выборочным данным. Например, ДИСП(10;14;5;6;10;12;13)равняется 11,667.

- Функция СТАНДОТКЛОН вычисляет стандартное отклонение. Например, СТАН-ДОТКЛ0Н(10; 14;5;6; 10; 12; 13)равняется 3,416.

- Функция ПЕРСЕНТИЛЬ позволяет получить квантили заданной выборки. Например, если ячейки А1:А7 содержат числа 10, 14, 5, 6, 10, 12 и 13, то квантилю со значением 0,1 является ПЕРСЕНТИЛЬ(А1:A7;0,1), равная 5,6.

Форму эмпирического распределения позволяют оценить специальные функции ЭКСЦЕСС и СКОС.

-Функция ЭКСЦЕСС вычисляет оценку эксцесса по выборочным данным. Например, ЭКСЦЕСС (10;14;5;6;10;12;13) равняется -1,169.

- Функция СКОС позволяет оценить асимметрию выборочного распределения. Например, СКОС(10;14;5;6;10;12;13) равняется -0,527.

Практические упражнения

Пример

Рассматриваются ежемесячные количества реализованных турфирмой путевок за периоды до и после начала активной рекламной компании. Ниже приведены количества реализованных путевок по месяцам.

С рекламой	Без рекламы

Требуется найти средние значения и стандартные отклонения этих данных.

Решение

1. Для проведения статистического анализа, прежде всего, необходимо ввести данные в рабочую таблицу. Отметим, что рассматриваемые группы данных со статистической точки зрения являются выборками.

2. При статистическом анализе, прежде всего, необходимо определить характеристики выборки, и важнейшей характеристикой является среднее значение. Для определения среднего значения в контрольной группе используйте функцию СРЗНАЧ. Определите в ячейке В9 среднее значение числа реализованных путевок без активной рекламы.

3. Следующей по важности характеристикой выборки является мера разброса элементов выборки от среднего значения. Такой мерой является среднее квадратичное или стандартное отклонение. Для определения стандартного отклонения в контрольной группе необходимо использовать функцию СТАНДОТКЛОН. В ячейке А10появится стандартное отклонение выборки — 12,298. Существует правило, согласно которому при отсутствии артефактов данные должны лежать в диапазоне М 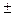З 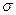(сигма) (в примере 145,7+36,9).

В ячейке В10 определить стандартное отклонение числа проданных путевок до начала рекламной компании.

Упражнения:

1. Найдите среднее значение и стандартное отклонение результатов эксперимента по теме диссертационного исследования:

2. Найдите выборочные среднее, медиану, моду, дисперсию и стандартное отклонение для следующей выборки 26, 35, 29, 27, 33, 35, 30, 33, 31, 29. (Можно заменить своей)