Наращенные суммы для финансовых рент

Обычная годовая рента. Пусть в конце каждого года в течение п лет на расчетный счет вносится по R рублей, сложные проценты на­числяются один раз в год по ставке i. В этом случае первый взнос к концу срока ренты возрастет до величины R(1+i ) n-1, так как на сумму R проценты начислялись в течение (n -1) года. Второй взнос увеличит­ся до R(1+i ) n-2 и т.д.

На последний взнос проценты не начисляются. Таким образом, в конце срока ренты ее наращенная сумма будет рав­на сумме членов геометрической прогрессии: S =R+R(1+i)+R(1+i)2+…+R(1+i) n-1 ,

в которой первый член равен R, знаменатель (1+i), число членов п.

Отсюда:

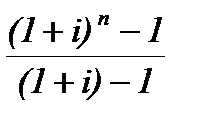S = R = R 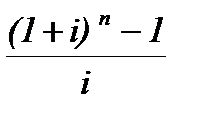= R sn ; i , (23)

где 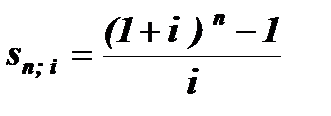- коэффициент наращения ренты. Он зависит только от срока ренты п и уровня процентной ставки i.

Рента р - срочная, с произвольным поступлением платежей p ≥ 1, и произвольным начислением процентов m ≥ 1 (общий случай). Это самый общий случай р-срочной ренты с начислением процентов т раз в году, причем, возможно, р ≠ т.

Первый член ренты R/p, уплаченный спустя 1/р года после нача­ла, составит к концу срока вместе с начисленными на него процента­ми

= .

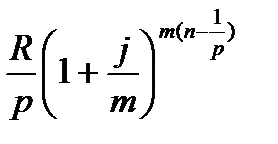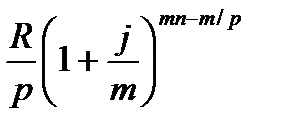Второй член ренты к концу срока возрастет до

= ,

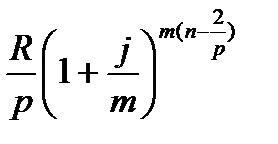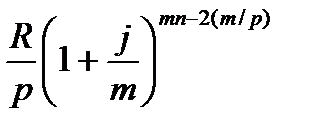и т.д.

Последний член этой записанной в обратном порядке геометриче­ской прогрессии равен R/p, ее знаменатель (1+j/m)m/p, число членов пт.

Для данного случая наращенная сумма рассчитывается по формуле:

S = 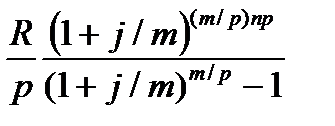= 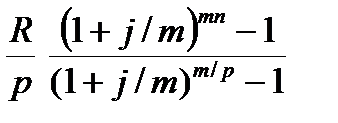. (27)

Из последней формулы легко получить все рассмотренные выше ча­стные случаи, задавая соответствующие значения р и т.

Определение величины отдельного платежа простой ренты

При определении величины отдельного платежа R возможны два случая: - известна наращенная сумма S,

- известна современная стоимость A.

1-й случай. Определение величины отдельного платежа при известной наращенной сумме S.

Когда известна наращенная сумма S, то платежи могут производиться по двум схемам:

- по схеме постнумерандо;

- по схеме пренумерандо.

Определение величины отдельного платежа по схеме постнумерандо. Если известны процентная ставка i, количество выплат п и наращен­ная сумма S простой рен­ты, то из формулы (23) можно определить величину отдельного платежа R:

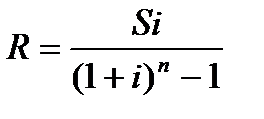. (28)

Определение величины отдельного платежа по схеме пренумерандо. Для простой ренты пренумерандо величина отдельного платежа R рассчитывается по формуле:

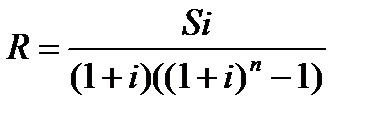. (29)

Определение величины отдельного платежа R по схеме постнумерандо. Когда известны процентная ставка i , количество выплат п и современная стоимость А (постнумерандо), то величину отдельного платежа R можно вычислить по формуле:

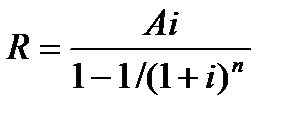. (30)