Решение задач оптимизации с помощью пакета Excel.

Лабораторная работа №2

Цель работы: овладение методами линейного программирования, нахождение экстремума линейных функций.

Тема для изучения: основные возможности обработки экономической информации на основе табличного процесса Excel.

Электронные таблицы Excel предназначены для упорядочения и обработки различных типов данных. Excel позволяет:

¨ Проводить сложные вычисления, как с использованием оригинальных расчетных формул, так и с применением стандартных математических, статистических, финансовых и иных функций;

¨ Осуществлять табличную обработку данных и представлять результаты расчетов в виде графиков и диаграмм;

¨ Планировать и распределять ресурсы;

¨ Составлять статистические сводки и калькуляции, проводить статистические финансовые расчеты.

Многие экономические задачи связаны с нахождением оптимальных решений при наличии некоторых ограничений на искомые переменные. Такие ограничения существенно уменьшают размеры области, в которой производится поиск оптимума. Решение подобных задач возможно с помощью надстройки Поиск решения.

В Excel реализованы методы математического программирования для решения задач линейного и нелинейного программирования.

Задачи линейного программирования относятся к числу наиболее часто решаемых задач оптимизации.

Формально задача линейного программирования понимается как задача поиска экстремума линейной целевой функции F на множестве, задаваемом системой линейных равенств и неравенств:

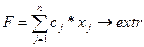
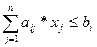
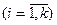
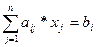
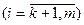
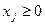
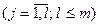
где a_ij, b_i, c_j – заданные постоянные величины и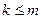

Для решения задачи используется Меню Сервис – Поиск решения. В открывающемся диалоговом окне «Поиск решения» необходимо указать:

¨ Адрес целевой ячейки

¨ Диапазон искомых ячеек

¨ Ограничения

Добавление, изменение и удаление ограничений производится с помощью кнопок Добавить, Изменить, Удалить.

Диалоговое окно «Результаты поиска решения» позволяет:

§ Сохранить на текущем рабочем месте найденное оптимальное решение;

§ Восстановить первоначальные значения и, внеся изменения, просчитать новый вариант;

§ Сохранить сценарий и анализировать содержащиеся в нем результаты;

§ Выдать отчеты по результатам устойчивости, пределам, необходимые для анализа найденного решения.

Для оценки влияния параметров на оптимальное решение необходимо произвести анализ чувствительности.

Отчеты по анализу чувствительности получают из окна «Результаты поиска решения» путем формирования отчетов:

ü результаты

ü пределы

ü устойчивость

Отчет по результатамсодержит следующие данные:

Ø сведения о целевой функции. В столбце исходно приводятся значения целевой функции до начала вычислений;

Ø значения искомых переменных;

Ø результаты оптимального решения для ограничений

В графе Формула приводятся зависимости, введенные в диалоговое окно «Поиск решения». В графе Значение приводятся величины использованного параметра. В графе Разница показывается количество неиспользованного параметра. Если параметр использован полностью, то в графе Состояние указывается связан, иначе – несвязан. Для граничных условий приводятся аналогичные величины с той лишь разницей, что в место неиспользованного ресурса показывается разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.

Отчет по пределам показывает, в каких пределах могут изменяться значения искомых переменных при сохранении структуры оптимального решения.

Отчет по устойчивости содержит сведения, показывающие степень зависимости решения от изменений величин, входящих в формулы.

Для нелинейных задач:

§ уменьшенный градиент показывает, на сколько увеличилось значение в целевой ячейке при увеличении значения в изменяемой ячейке на 1;

§ множитель Лагранжа показывает, на сколько увеличится значение в целевой ячейке при увеличении ограничения на 1.

Для линейных задач:

По каждой изменяемой ячейке:

§ уменьшенная стоимость – заменяет уменьшенный градиент;

§ целевой коэффициент показывает, относительную взаимосвязь между изменяемой ячейкой и целевой ячейкой;

§ допустимое увеличение показывает, изменение целевого коэффициента до момента убывания оптимального значения в любой из изменяемых ячеек.

По каждой ячейке ограничений приводятся:

§ теневая цена – заменяет множитель Лагранжа;

§ ограничение. правая часть содержит список заданных значений ограничений;

§ допустимое увеличение показывает изменение значения правой части ограничения до момента приращения оптимального значения в любой из изменяемых ячеек;

§ допустимое убывание показывает изменение значения правой части ограничения до момента убывания оптимального значения в любой из изменяемых ячеек.

Отчет по ограничениям

В отчете по ограничениям выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.

¨ нижний предел – это наименьший из удовлетворяющих ограничение значений, которое может принимать изменяемая ячейка при сохранении фиксированных значений всех остальных изменяемых ячеек

¨ верхний предел – это наибольшее из удовлетворяющих ограничение значений, которое может принимать изменяемая ячейка при сохранении фиксированных значений всех остальных изменяемых ячеек

¨ целевой результат – значение, полученное в целевой ячейке при условии, что значение изменяемой ячейки равно нижнему или верхнему пределу.

ПРАКТИЧЕСКАЯ ЧАСТЬ

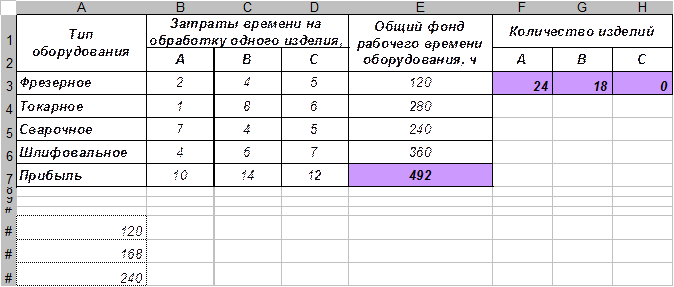
Задача 1. Для изготовления трех видов изделий А, В, С используется токарное, сварочное и шлифовальное оборудование. затраты времени на обработку одного изделия для каждого типа оборудования указаны в таблице.

Требуется определить, сколько изделий и какого вида следует изготовлять предприятию, чтобы прибыль от реализации была максимальной.

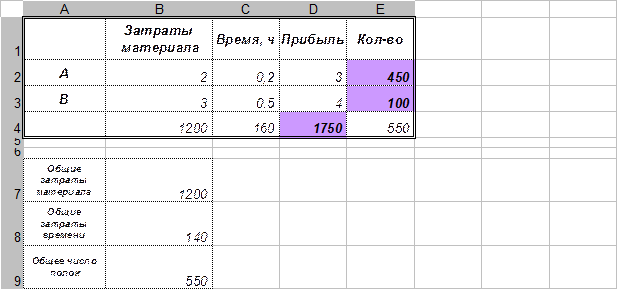
Задача 2. Компания производит полки для ванных комнат двух размеров А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. для каждой полки типа А требуется 2 м материала, а для полок типа В – 3 м материала. Компания может получить до 1200 м материала в неделю. для изготовления полки типа А требуется 12 мин машинного времени, а для одной полки типа В – 30 мин; ресурс машинного времени в неделю составляет 160 ч. если прибыль от продажи полок типа А составляет 3$, а от типа В – 4$, то сколько полок каждого типа следует выпускать в неделю.

Задача 3. Автозавод выпускает две модели: «Каприз» и «Фиаско». На заводе работает 1 000 неквалифицированных и 800 квалифицированных рабочих, каждому из которых оплачивается 40 часов в неделю. Для изготовления модели «Каприз» требуется 30 ч неквалифицированного труда и 50 квалифицированного труда; для «Фиаско» соответственно 40 и 20 ч. Каждая модель «Фиаско» требует затрат в размере 500$ на сырье и комплектующие изделия, «Капрз» - 1 500$; суммарные затраты не должны превосходить 900 000$ в неделю. Рабочие, осуществляющие доставку, работают по 5 дней и могут забрать с завода не более 210 машин в день. Каждая модель «Каприз приносит прибыль – 1 000$, «Фиаско» - 500$. Какой объем выпуска каждой модели Вы порекомендуете.