Репрезентативность выборки для проведения опроса

Основной принцип исследований “по выборке” состоит в получении информации о всей популяции по сравнительно небольшой выборке из нее. Размер выборки определяет точность полученных результатов.

Классический метод создания исследуемой выборки - случайный отбор. Для исследований потребителей обычно используется список избирателей, из которого набирается выборка по случайным цифрам или “каждый первый”. Объем выборок обычно порядка нескольких сотен или тысяч (например, для Англии обычно берется около 30000, т.е. примерно тысячная часть взрослого населения).

При принятии нормального закона распределения среднеквадратичное отклонение определяется так:

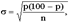
где p - процент популяции, имеющий признак, подлежащий измерению;
n - объем выборки.

Например, в выборку включены 1000 домовладельцев и мы нашли, что 10% из них соответствуют измеряемому признаку, тогда

Это означает, что с вероятностью 68% (одно стандартное отклонение) можно утверждать, что результат лежит между 9,7 и 10,3%, а при допустимой вероятности 0,95 - между 9,4 и 10,6% (два ), а если n = 400, то в последнем случае границы 7-13% (стандартное отклонение 1,5%). Поэтому часто принимают необходимый объем выборки в 1000 респондентов (см. табл. 2.9).

Очевидно, что абсолютный уровень ошибки - наивысший при p=50%, например, при n = 400 и допустимой вероятности правильного ответа 0,95 =2,5% и границы действительных результатов 45-55%. Иными словами, чем меньше ясно респондентам решение (50/50 - наихудший вариант), тем меньше точность. В этих случаях надо увеличивать выборку (увеличение выборки в два раза приводит к увеличению точности в раза). Еще раз следует подчеркнуть, что эти оценки справедливы для действительно случайной выборки.

Таблица 2.9

Диапазоны точности при различных объемах выборки

Размер выборки	Ожидаемый результат (%) при уровне согласия 0,95
	10 или 90 (±)	30 или 70 (±)	50 (±)
	9 (4,5)	13 (6,5)	14 (7)
	6 (3)	9 (4,5)	10 (5)
	4 (2)	6 (3)	7 (3,5)
	3 (1,5)	4 (2)	4 (2)
	2 (1)	3 (1,5)	3 (1,5)
	1 (0,5)	1 (0,5)	1 (0,5)

Собранные статистические данные могут анализироваться различным образом. Например, с использованием многомерного регрессионного анализа, факторного анализа, кластерного анализа и анализа связей.

Ошибки репрезент-ти свойственны несплошному наблюдению. Возникает в резте выборочного наблюдения, когда отобранная часть единиц сов-ти недостаточно полно отражает состав всей изучаемой сов-ти. М.б.случайными (оцениваются с помощью математ.м-ов) и систематическими (отклонения,кот.возник-ют в рез-те случ.отбора единиц изуч-ей сов-ти, их размеры не поддаются кол-ой оценке). Для выявления и устранения допущенных при регрессии ошибок примен-ся след.м-ды:

1.внешний конторль (проверяется правильность оформления документов; наличие всех необход-х записей, кот.пред-ны инструкцией и т.д.);

2.логический контроль (проверка ответов на вопросы программы наблюд-я путем сопоставления получ-х данных с другими инст-ми);

3.счетный контроль (счетная проверка всех итоговых показ-ей, кот.содержатся в отчет-ти или формуляре исследования, задачей такого контроля явл.исправление итогов и отдел.числит.показ-ей). В ряде случаев, при счетном контроле данных применяется м-д балансовой увязки показателей (наличие на начало отчет.периода + поступления – расход должно быть равно наличию на конец отчет периода). Указ.м-ды проверки достоверности позволяют сократить до минимального значения допуск ошибок.