Краткие методические указания к решению задачи 1.10.

Под математическим выравниванием частот эмпирического ряда в общем случае понимается замена его теоретическим рядом распределения, имеющим определенное аналитическое выражение (параметры последнего определяются по данным эмпирического ряда).

В практике статистического исследования приходится встречаться с самыми различными распределениями. Наиболее распространенными является нормальное распределение. Для того, чтобы построить нормальное распределение достаточно располагать двумя статистическими характеристиками – и , расчеты которых неоднократно проводилась в предшествующих задачах данной работы.

Кривая нормального распределения выражается уравнением:

,

где – ордината кривой нормального распределения; , e – математические константы, = 3,1416; e = 2,7132 – основание натурального логарифма.

В этом уравнении рассматривается как функция t, то есть каждому значению t соответствует определенное значение .

Например, если t = 0, то .

Так как = 1; при t = 1; .

Точечная функция затабулирована и представлена во всех учебных пособиях по теории статистики как приложение (таблица значений распределения вероятностей в случае нормального распределения).

Последовательность расчета теоретических частот по этой формуле сводится к следующему:

1. Рассчитывается средняя арифметическая ряда ;

2. Рассчитывается среднеквадратическое отклонение σ;

3. Находится нормированное отклонение каждого варианта от средней арифметической т.е. ;

4. Для найденных t по таблице значений: находится (теор);

5.Рассчитывается константа ;

6. Каждое значение (1) умножается на константу const.

Результаты умножения (после округления до целых чисел) будут искомыми частотами теоретической кривой распределения.

После выравнивания ряда, т.е., исчисления теоретических частот возникает необходимость в проверке, «случайности» или «не случайности» расхождения между эмпирическими и теоретическими частотами, и тем самым проверки правильности выдвинутой гипотезы об обоснованности нормального распределения. В этих целях рассчитываются критерии согласия:

а) критерии согласи Пирсона: .

Полученные результаты расчетов значение 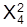сравнивается с табличным значением при принятом уровне значимости (0,10; 0,05; 0,01) к заданным числом степеней свободы (см. в приложениях к учебным пособиям таблицу значений, t-критерий). Число степеней свободы определяется как число групп в ряду распределения минус число параметров и минус единица: K-n-1.

При определении нормального распределения используется 2 параметра – это , и σ, т.е., если К = 6, то число степеней свободы определяется 6 – 2 – 1 = 3;

Если фактическое значение оказывается меньше табличного, то расхождение между эмпирическими и теоретическими частотами признается случайным и распределение не отвергается;

б) критерий Романовского

Если значение критерия Романовского меньше 3, то можно считать расхождение между эмпирическими и теоретическими частотами случайным;

в) критерий Колмогорова

,

где d – максимальная разность между накопленными эмпирическими и теоретическими частотами; n – число единиц совокупности.

При принятом уровне значимости и заданном числе степеней свободы по специальной таблице значений Функции Колмогорова определяется расчетное значение критерия, которое сопоставляется с расчетным. Ниже представляется последовательность расчетов и их результаты.

В расчете использованы следующие статистические характеристики: ; ; i = 1500.

Таблица 26

Последовательность расчета теоретических частот φ

№	Нижние и верхние границы интервалов	Эмпирические частоты f	Серединные значения интервалов	Нормируемые отклонения	φ(t)	Теоретические частоты φ
I	3000–4500			–1,77	0,083172
II	4500–6000			–1,06	0,228439
III	6000–7500			–0,34	0,376391
IV	7500–9000			0,37	0,372036
V	9000–10500			1,09	0,220600
VI	10500–12000			1,80	0,078469
ИТОГО		–	–	–

Рис. 2. Эмпирические и теоретические распределения частот

Таблица 27