Краткие методические указания к решению задачи 1.2.
Расчет показателей по индивидуальным данным проводится по каждому признаку – Х1, Х2, Х3 и Х4 в следующей последовательности:
1. Определяются итоговые обобщающие показатели, т.е. производится расчет сумм для каждого из признаков в отдельности:
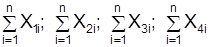 ,
,
где i = 1…n; n – число единиц наблюдения.
2. Рассчитываются простые средние арифметические величины:
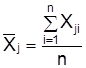 ,
,
где j = 1…; m – число признаков; 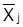 – простая среднеарифметическая величина j-го признака;
– простая среднеарифметическая величина j-го признака; 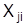 – индивидуальные значения j-го признака i-ой единицы наблюдения.
– индивидуальные значения j-го признака i-ой единицы наблюдения.
3. Рассчитываются показатели размаха вариации;
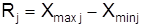 ,
,
где 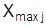 – максимальное значение j-го признака;
– максимальное значение j-го признака; 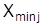 – минимальное значение j-го признака.
– минимальное значение j-го признака.
4. Рассчитываются средние линейные отклонения:
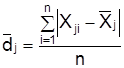 .
.
5. Рассчитываются дисперсии:
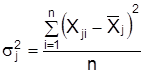 .
.
6. Рассчитайте среднеквадратические отклонения:
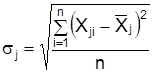 ,
,
где i = 1…n, j = 1…m.
7. Определяются в относительных величинах коэффициенты вариации:
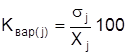 .
.
При проведении расчетов по вышеприведенным формулам целесообразно использовать вспомогательные расчеты таблицы, в которых представляется последовательность арифметических действий и все промежуточные результаты.
Например, при расчете средних величин, средних линейных отклонений и дисперсий для каждого признака (по условиям задачи) промежуточные таблицы могут быть представлены следующим образом:
| № п/п | Х (1) |  (2) (2) | 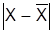 (3) (3) | 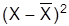 (4) (4) |
| … | ||||
| N | ||||
| Итого | 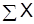 | 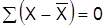 | 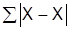 | 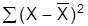 |
Полученные в результате расчетов обобщающие статистические характеристики оформляются в виде выходных статистических таблиц.
Ниже для иллюстрации нами приводятся результаты расчетов этих характеристик отдельно для количественных признаков – Х1, Х2, и Х3 (непрерывные признаки – Х1 и Х2 и дискретный признак Х3) и для альтернативного признака Х4, выполненные по данным информационной таблицы базового варианта (см. введение).
Основные статистические характеристики количественных признаков – Х1, Х2, Х3 представлены в табл. 3.
Таблица 3
| № п/п | Характеристики. Признаки | Х1, руб. | Х2, руб. | Х3, руб. |
| Итоговые обобщающие показатели | ||||
| Средние величины | 7465,83 | 3663,00 | 3,73 | |
| Размах вариации | ||||
| Средние линейные отклонения | 1732,2 | 747,87 | 0,93 | |
| Дисперсии | 4403140,14 | 834847,67 | 1,26 | |
| Средние квадратических отклонений | 2098,37 | 913,70 | 1,12 | |
| Коэффициент вариаций в % | 28,11 | 24,94 | 30,09 |
Основные статистические характеристики альтернативного признака – Х4.
Таблица 4
| № п/п | Характеристики. Признаки. | Х4 |
Сумма единиц, обладающая данным признаком  | ||
Доля единиц, обладающая данным признаком 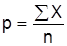 | 0,50 | |
| Доля единиц, не обладающая данным признаком = (1 – p) | 0,50 | |
Дисперсия альтернативного признака 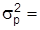 pq pq | 0,25 | |
Среднеквадратическое отклонение альтернативного признака 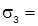 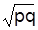 | 0,25 |
Представленные выходные таблицы в этой и всех последующих задачах носят рекомендательный характер, так как возможны и другие формы представления данных.
В целях упрощения нумерация формул, таблиц, графиков дается по каждой задаче в отдельности.
Задача 1.3
По данным информационной таблицы Вашего варианта произведите группировку индивидуальных данных, приняв за основу группировки количественный непрерывный признак Х1. Группы образуйте с равными и неравными интервалами в следующей последовательности.
1. Образуйте группы с равными интервалами. По каждой группе определите:
а) число единиц наблюдения в абсолютных и относительных величинах (в % к итогу);
б) групповые обозначающие итоговые показатели признаков – Х1, Х2, Х3, Х4 в абсолютных и относительных величинах (в % к итогу);
в) групповые средние величины и групповые частные дисперсии признаков – Х1, Х2, Х3, Х4.
2. Образуйте группы с неравными (равнонаправленными) интервалами – 10 групп по 10% единиц наблюдения в каждом интервале и 5 групп по 20% единиц наблюдения также в каждом интервале. По каждой группе для признаков Х1, Х2, Х3, Х4 (для названных вариантов) рассчитайте групповые итоговые значения названных признаков в абсолютных и относительных величинах (в % к итогу).
3. Образуйте 5 групп с интервалами, меняющимися по правилу арифметической прогрессии. Рассчитайте абсолютные и относительные показатели плотности распределения. Все полученные результаты (пункты 1, 2, 3) представьте в статистических таблицах.
