Последовательность действий при отрицательных результатах поиска решения
На практике при решении задач линейного программирования часто не удается получить оптимального решения. Это может по двум следующим причинам:
- ограничения несовместны, либо из-за неправильной математической модели, либо из-за неправильных исходных данных. В таких случаях Excel будет выдавать сообщение «Поиск не может найти подходящего решения»;
- целевая функция не ограничена сверху (при максимизации ЦФ) или снизу (при минимизации ЦФ). Неограниченность ЦФ – следствие ошибки в математической модели. В этом случае ЭТ Exce будет выдавать сообщение «Значения целевой ячейки не сходятся».
Рассмотрим последовательность действий пользователя в случаях не нахождения программой подходящего решения.
2.1.1. Если условия несовместны, на экране появляется диалоговое окно с сообщением, что поиск не может найти подходящего решения (Рис. 2.1.1).
2.1.2. Как следует поступать, если условия задачи оказались несовместными? Для получения несовместности в учебных целях изменим условия задачи. В полученном оптимальном решении было определено, что для выпуска 10 единиц Прод1 и 6 единиц Прод3 трудовые ресурсы и финансы будут использованы полностью. Дополнительно назначим необходимость выпуска ещё 5 единиц Прод2. Очевидно, что для выпуска такого количества продукции ресурсов будет недостаточно. Внесем соответствующие изменения в условия задачи и рассмотрим последовательность действий по преодолению несовместности.
2.1.2.1. Вызовите исходную таблицу (рис. 1.4.2).
2.1.2.2. Вызовите диалоговое окно Поиск решения (п.4.1.11 и далее).
2.1.2.3. В окне Ограничения удалите строку $B$3:$E$3 >= В4:Е4.
2.1.2.4. С помощью кнопки Добавить поочередно введите три новых ограничения – В3 = 10; С3 = 5 и D3 = 6. Введя эти три ограничения;
2.1.2.5. Нажмите клавишу Выполнить. На экране появится окно, представленное на рис. 2.1.3.
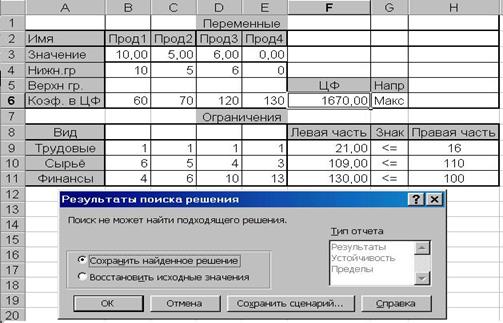
Рис. 2.1.1
2.1.2.6. Вы видите, что полученное решение не является даже допустимым, т.к. левые части ограничений, т.е. потребное количество ресурсов, превышает имеющееся их количество - правые части.
Из рисунка видно, что для заданного выпуска продукции необходимо иметь всего следующее количество ресурсов:
- трудовые - 21 единицу;
- сырьё - 109 единиц;
- финансы - 130 единиц.
При этом будет получена прибыль в 1670 единиц.
Если в реальных условиях нет возможности увеличить ресурсы, нужно решать исходную задачу при граничных условиях xj ³ 0, и тогда будет получено решение, которое определяется имеющимися ресурсами.
2.1.3. Как уже указывалось, программа не может найти подходящее решение и тогда, когда не заданы ограничения целевой функции. В этом случае на экране появляется следующее диалоговое окно (Рис. 2.2.1).
Рис. 2.2.1
«Значения целевой ячейки не сходятся» в том случае, когда область допустимых решений не имеет ограничения, препятствующего бесконечному возрастанию (убыванию) целевой функции.
Для преодоления этой неограниченности необходимо следить, чтобы при максимизации целевой функции область допустимых решений была ограничена сверху, а при минимизации – снизу.
