Ипотечная схема первичного рынка недвижимости

Приведенный выше пример ипотеки имеет одно весьма важное условие. Объект недвижимости на момент оформления ипотечной ссуды подразумевался готовым к эксплуатации. В современных условиях очень часто ипотечное кредитование применяется к еще строящимся объектам. При этом, очевидно, что у кредитора возрастают риски по возврату ссуды, поскольку залог не имеет полной потребительской ценности. Значительную роль в этом случае приобретают риски кредитора, обусловленные в первую очередь вероятной неплатежеспособностью ссудо-заемщиков и, как следствие, возникновением проблем по возврату ссуды, ведущих при негативных обстоятельствах к расторжению отношений по кредитованию. Ипотечный залог в период незавершенного строительства представляет собой часть (долю незавершенного строительства) несданного в эксплуатацию объекта недвижимости и поэтому не обладает высокой стоимостью и ликвидностью что усугубляет риски кредитора.

С другой стороны, такие ипотечные схемы могут оказаться привлекательными, поскольку позволяют кредитным организациям осуществлять кредитование производственного, а не спекулятивного сектора. Наибольшие плюсы от такого рода ипотечных схем, вероятно, пожинают строители, поскольку такие схемы позволяют им осуществлять основную деятельность – вести строительство достаточно крупных объектов. Нельзя не упомянуть и очевидную пользу от расширения поля потребителей недвижимости за счет участия клиентов не имеющих достаточных средств для одномоментного приобретения недвижимости и залога для оформления кредита.

Рассмотрим пример схемы ипотечного кредитования с условием того, что ссуда долгосрочная, то есть срок ссуды заканчивается позже срока сдачи недвижимости в эксплуатацию. В этом случае для снижения рисков по возврату ссуды для кредитора, до сдачи недвижимости в эксплуатацию бремя обеспечения гарантий по возврату ссуды может быть возложено на организацию, осуществляющую строительство недвижимости (рис. 10.4а). При этом логично напрямую предоставлять средства от кредитора строителям, относя бремя по возврату затрат кредитора по строительству на будущего владельца недвижимости/участника ипотечной схемы.

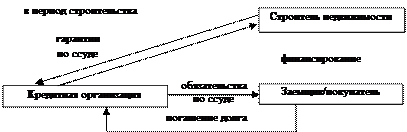Рис. 10.4а

После завершения строительства и сдачи недвижимости в эксплуатацию из этой схемы естественным образом исключается участник, осуществивший строительство. Схема взаимодействия кредитной организации с потребителями (рис. 10.4б) сводится к схеме классического кредитования БАНК-КЛИЕНТ с залогом недвижимости в качестве обеспечения возврата кредитной организации вложенных в проект средств.

Рис. 10.4б

Рассмотрим простейшую схему платежей ипотечного кредитования. График финансовых потоков такой схемы будет выглядеть следующим образом (рис. 10.5).

поток 1

поток 2

Рис.10.5

Поток платежей 1 Z_m представляет собой график финансирования строительства, который для простоты будем полагать ежегодным в течении n₀ лет. Поток платежей 2 Rm является суммарными платежами будущих потребителей недвижимости по погашению расходов Банка по финансирования строительства так же для простоты будем считать ежегодным в течении n лет.

Пусть нашелся Банк, который согласен обеспечить финансирование строительства в относительно короткие сроки (n₀ лет), и принимать взносы от будущих владельцев недвижимости в течении более долгого срока (n лет). С точки зрения Банка для участия в таком проекте необходимо соблюсти свои финансовые интересы. Действительно, принимая управленческое решение о выделении средств на финансирование ипотечного проекта Банку нет экономического смысла закладывать ставку доходности меньшую, чем средняя ставка доходности по Банку. Как правило, в качестве такой ставки выбирают среднюю ставку доходности ресурсов по Банку i_банка, если на то нет веских конъюктурных причин.

Таким образом, прогнозируя свое участие в проекте, Банк должен убедиться в отсутствии упущенной выгоды за весь период участия в проекте. То есть оценить по средней ставке доходности банка i_банка доходы, которые мог бы принести поток средств 1 к Z_m концу проекта (через n лет) и сравнить их с доходами, которые принесет поток платежей 2 R_m за тот же период времени. Очевидно, что они должны быть равны или же доходы от потока 2 могут быть больше.

Охарактеризовать доход от обоих потоков можно наращенной суммой S₁ и S₂ этих потоков к концу срока проекта n лет. В предположении того, что Банк вместо финансирования строительства пустил средства потока 1 в оборот по средней ставке доходности банка i_банка найдем наращенную сумма S₁ концу срока ипотечного проекта (n лет). Это та сумма средств, которая может оказаться в распоряжении Банка, если средства выделенные на финансирование строительства (поток 1 к Z_m) использовать в других банковских операциях со ставкой доходности iбанка. Ее величину S₁ можно определить в два этапа:

1. Платежи Z_m можно рассматривать как ренту сроком n₀ лет, которую можно охарактеризовать одной из ее обобщенных характеристик, а именно наращенной суммой (лекция 8, (8.10)). Величина наращенной суммы потока равных по величине платежей Z = Z_m, где m = 1, 2, 3, ..., n₀ на дату окончания финансирования строительства n₀ будет равна

S = Z ´ (qⁿ – 1)/(q – 1), (10.1)

где q = (1 + i_банка).

То есть выражение (10.1) представляет собой ту сумму средств, которую имел бы в своем распоряжении Банк на дату n₀, размещая платежи Z_m по ставке iбанка.

2) Далее Банк эту наращенную сумму S так же может разместить на срок до конца ипотечного проекта на n – n₀ лет под ту же среднюю ставку доходности i_банка, то есть искомая сумма S₁ потока платежей 1 Z_m будет равна

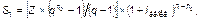(10.2)

где q = (1+ i_банка).

Сумма S₁ это объем средств, которые мог бы получить Банк от альтернативного ипотечному проекту размещения средств Z_m по ставке i_банка. Иначе говоря возможная выгода Банка от вложения средств Z_m. То есть величина S₁ – является основной характеристикой, которая в дальнейшем определяет требования Банка по получению своей выгоды при уплате будущими клиентами взносов за недвижимость. Именно на ее величину должен ориентироваться Банк, поскольку получив в свое распоряжение меньшую сумму Банк окажется в состоянии упущенной выгоды.

Поток платежей 2 должен возместить Банку затраченные на строительство средства. Этот поток 2 так же можно рассматривать как ренту, наращенная сумма которой к концу срока n должна быть равна (или больше) величине S₁. Значение величины самих платежей R, которые собственно являются потоком 2, так же можно определить из соотношения (10.2) записанного применительно к потоку 2

S₂ = R ´ (qⁿ – 1)/(q – 1), (10.3)

где q = (1 + i) и S₂ = S₁,

которое определяет величину наращенной суммы потока платежей 2 в течении n лет (см. лекцию 8, (8.10)), а величина платежей R будет равна

R = S₁ ´ (q – 1)/(qⁿ – 1).

Следует отметить, что при найденном из (10.2) значении S₁ ограничений на значение ставки i, числа лет n, величину взносов R в выражении (10.3) нет. Однако это не означает, что сами значения i, n, R, удовлетворяющие соотношению (10.3) могут быть произвольными. Каждый из параметров i, n, R, имеет область допустимых значений, отражающих экономический смысл в ипотечном проекте. Прокомментируем роль каждого из параметров i, n, R с точки зрения влияния на ипотечный проект. Так величина n – число лет в течение которого клиенты будут возмещать Банку его затраты на строительство, не может и не должна превышать платежеспособный срок жизни клиента. Для разных возрастных категорий экономически активного населения он колеблется от 5 до 25 лет. Ставка i в выражении (10.3) это ставка доходности по которой Банк планирует размещать поступающие от клиентов взносы R для того, чтобы к окончанию ипотечного проекта компенсировать свои затраты на финансирование строительства с учетом сохранения средней доходности по Банку (по ставке i_банка). Следует отметить, что формально значение ставки i может быть как больше, так и меньше значения i_банка. Главный вопрос для Банка как можно точнее спрогнозировать на достаточно большой срок n лет возможность размещения средств R под выбранную ставку доходности i. При этом очевидно, что чем выше значение ставки i, тем «легче» (быстрее и дешевле для клиента, а следовательно надежней) для Банка компенсировать свои затраты по строительству. На величину ежегодных взносов клиентов R так же нет формальных ограничений, за исключением требований потребительской привлекательности, поскольку очевидно, что высокие платежи R отпугнут клиентов от участия в таком проекте. Параметры i, n, R, связаны между собой, то есть два любых могут быть заданы, а третий определен из (10.3).

ПРИМЕР. Пусть срок строительства n₀ = 3 года, средняя ставка доходности ресурсов Банка i_банка = 11%, необходимый для поддержания строительства ежегодный взнос Z = 10 000 000 руб., а общий срок ипотечного проекта n = 10 лет. Тогда, согласно (10.2) S₁ = 69 387 348,47 руб. Для простоты значение ставки i сохраним такой же, как средняя доходность ресурсов банка i = i_банка = 11%. Из (10.3) определим величину необходимого ежегодного взноса R = 4 149 462,46 руб.

После приведенных расчетов Банк может предложить некоторое бизнес-предложение:

«Профинансируем строительство Проекта общей стоимостью 30 млн. руб. ежегодными, равными платежами в течение 3-х лет, на условиях ипотеки, с погашением затрат в течение 10 лет ежегодными, равными платежами в 4 149 462,46 руб.».

Не трудно убедиться, что с параметрами приведенного предложения нелегко согласиться обывателю, который арифметически подсчитает, что «за Проект стоимость 30 млн придется заплатить почти 41,5 млн, т.е. переплатить около 38%». Это бытовая логика и с ней приходится считаться.

Отметив для себя это обстоятельство все таки детализируем бизнес предложение банка. Согласно современным ценам 30 000 руб. за 1 м². Проект может представлять собой дом площадью 1 000 м², на которых можно разместить 10 квартир по 100 м². Следовательно, для каждого из 10 клиентов доля в ежегодном платеже составит P_г = 414 964,5 руб. Напрямую накопить такую сумму за год в «чулке» от первого до последнего взноса можно ежемесячными взносам Pм величиной 34 587,37 руб. Сумма огромная и охотников участвовать в таком проекте найдется не много.

Традиционный способ «борьбы за привлечение клиента» лежит на пути снижения очевидных для восприятия клиента параметров финансовых отношений. Например, удлинить срок выплаты задолженности n, а также в одностороннем порядке Банку умерить свои аппетиты по собственным доходам, то есть снизить величину процентной ставки планируемой доходности iбанка поскольку широко бытует представление (и не без оснований), что такие меры облегчают бремя финансовых обязательств клиента.

Рассмотрим пример такого облегчения текущего финансового бремени клиента.

Пусть срок ипотечного проекта остался неизменным n = 10 лет, а ставка планируемой Банком доходности снизилась до i_банка = 5%, тогда из (10.2) S₁ = 44 358 840,82 руб., ежегодный взнос в погашение затрат на строительство согласно (10.3) будет равен Pг = 3 526 730,79 руб., вместо 4 149 462,46 руб., т.е. уменьшился на 15% и, следовательно, ежемесячный «чулочный» взнос отдельного клиента так же снизится на 15% и составит P_м = 29 389,42 руб. То есть при снижении ставки i_банка более чем на 50% платежи клиентов уменьшились лишь на 15%. Жертва в ставке на 50% со стороны Банка не кажется адекватной 15%-му снижению клиентского платежа.

Изменим другой параметр – общий срок ипотечного проекта. В случае увеличения в два раза срока ипотечного проекта n = 20 лет при той же ставке доходов Банка i_банка = 5% величина S₁ = 72 255 877,47 руб., а ежегодное возмещения затрат строительства составит P_г =2 185 204,67 руб., т.е. понизится по сравнению с предыдущим случаем (n = 10, i_банка = 5%) еще на 38%, а ежемесячный «чулочный» взнос одного клиента составит P_м = 18 210,04 руб. Общее «смягчение» условий по ипотечному проекту в виде снижения ежегодного взноса на возмещение затрат строительства составил порядка 47%. То есть увеличение в два раза срока выплат по ипотеке и снижение ставки своей доходности со стороны Банка более чем в два раза привело к уменьшению ежемесячного «чулочного» платежа отдельного клиента на 47% и составило 18 210,04 руб., что по силам уже более широкому кругу клиентов. Пострадавшей стороной при таких изменениях параметров ипотечного проекта оказался Банк (вследствие снижения ставки доходности до 5%), однако при этом обеспечена стабильность денежного потока на 20 лет и на 4% увеличился общий объем участвующих в проекте денежных средств с S₁ = 69 387 348,47 руб. (при n = 10, i_банка = 11%) до S₁ = 72 255 877,47 руб. (при n = 20, i_банка = 5%).

Следует отметить, что выше для простоты был предложен «чулочный» способ накопления требуемого ежегодного платежа в размере Pг = 2 185 204,67 руб. Если ежемесячные накопительные взносы P_м не копить в «чулке», а разместить под некоторую ежемесячную ставку im до момента выплаты ежегодного ипотечного платежа P_г, тогда итоговая сумма накопительных взносов P_м возрастет за счет начисляемых по ставке im процентов. Следовательно саму величину ежемесячных взносов P_м для обеспечения суммы P_г = 2 185 204,67 руб. при таком (не «чулочном») способе накопления можно понизить. Для нахождения этого нового ежемесячного платежа P_{клиента} так же воспользуемся выражением для наращенной суммы ренты (10.3), понимая под ставкой ежемесячную ставку i_m, с ежемесячным начислением сложных процентов, а под общим сроком этой промежуточной ренты будем понимать сок до уплаты ежегодного платежа то есть m = 12 месяцев. Тогда величина ежемесячного платежа P_{клиента} найдется из выражения

P_{клиента} = P_г ´ (q – 1)/(q^m – 1), (10.4)

где q = (1 + i_m).

Остается определиться со значением месячной ставки i_m сложных процентов, оценить какой величины она может быть? Это можно сделать, основываясь на предложении некоторых банков о размещении депозита под годовую ставку i с возможностью увеличивать сумму депозита в течение срока депозита. Величина такой ставки на сегодня вряд ли превышает 10% годовых. Пользуясь формулами условий эквивалентности ставок (см. лекцию 6) простой годовой ставки i и сложной месячной ставки i_m получаем соотношение

(1 + i) = (1 + i_m)^m, (10.5)

где m = 12, i = 0,1, из которого легко найти i_m=0,79%.

Таким образом из (10.4) находим новое значение ежемесячного платежа отдельно взятого клиента P_{клиента} = 17 263,11 руб., т.е. размещение ежемесячных взносов отдельного клиента на накопительный депозит с простой годовой ставкой i = 10% привело к снижению величины ежемесячного платежа этого клиента на 5,2%.

Для полноты картины приведем еще один исключительный, но вполне вероятный вариант. Банк при прогнозе возможного размещения средств Z заложил ставку i_банка = 5%, а в дальнейшем по факту размещения уплачиваемых клиентами средств R стало возможным осуществлять размещение средств под увеличенную ставку i = 10% годовых. Такая ситуация вероятна при изменении в лучшую сторону конъюктуры размещения средств или при сознательном отказе Банка от получения доходов по уровню максимально возможной доходности. То есть при зафиксированном плане по доходности сами возможности доходности возросли и принято решение использовать этот «неожиданный» фактор во благо клиентов. Ответ на вопрос «насколько реален такой сценарий?» остается за пределами компетенции автора.

В рамках сделанных выше оговорок рассмотрим ипотечный проект, предусматривающий финансирование строительства ежегодными платежами Z = 10 000 000 руб. в течении n₀ = 3 лет при принятой Банком ставке доходности i_банка = 5%. Общий срок ипотечного проекта n = 20 лет, ставка размещения ежегодных взносов клиентов i = 10%. В этом случае величина S₁ согласно подсчетам (см. (10.2)) будет составлять S₁ = 72 255 877,47 руб., при этом величина ежегодных взносов клиентов (см. (10.2)) составит R = 1 261 560,51 руб. Таким образом ежемесячный «чулочный» взнос одного клиента будет равен P_м = 10 513 руб., который можно снизить на 5% используя накопительный депозит с годовой ставкой i = 10%, то есть до величины P_{клиента} = 9 987,35 руб., что является вполне приемлемой цифрой для семейного бюджета в 20–25 тыс. руб. в месяц.

Возвращаясь к «бытовой логике, с которой приходится считаться» арифметическая сумма затрат при ипотечной покупке объекта стоимостью 30 млн составит 23 969 640 руб., т.е. на 20% дешевле. Не смотря на то, что безнравственно смешивать финансовые расчеты и бытовую логику сплошь и рядом для рекламных целей встречаются «коктейли» из умело переплетенных данных бытовой логики и точных финансовых расчетов. Вынужденно встав на эту точку зрения в рекламных целях, аналитикам, рассчитывающим точные финансовые схемы ипотеки, есть смыл подобрать такие параметры (i, n, R и др.) которые приемлемо выглядят и в свете бытовой логики. Например такие, которые формально уравнивают стоимость объекта с суммой затрат, подсчитанную бытовой логикой. Резон сделать это состоит еще и в том, что бы максимально приблизится грани соблюдения реальных финансовых интересов Банка, поскольку облегчение финансового бремени клиента так или иначе происходит за счет недополученной выгоды остальных участников, как в приведенных выше примерах. Банк, вообще говоря, мог бы и не участвовать в ипотечном проекте на столь невыгодных условиях.

Следует отметить, что, рассматривая интересы участников через призму приведенных выше финансовых параметров ипотечного проекта, ключевым участником является Банк. Основной параметр, который интересует Банк это ставка доходности, уровень которой Банк определяет для себя сам. В какой–то мере Банк заинтересован в объемах и сроках фигурирующих в ипотечном проекте средств, но только в качестве «второго эшелона», производной от оборота в виде не основных для банковской деятельности, дополнительных операционных доходов.

Основная «головная боль» другого участника – Строительной организации – это стабильность (регулярность и полнота) финансирования строительных работ, что определяется, прежде всего, устойчивостью Банка в не очень продолжительный период строительства.

С учетом сказанного основное внимание при анализе будущих параметров ипотеки, в первую очередь, должно быть направлено на интересы будущего владельца недвижимости, то есть клиента, поскольку его интересы наиболее легко уязвимое звено. Клиент не может непосредственно влиять в своих интересах на формирование условий по ипотеке и этим обусловлена его категоричность в выборе «участвовать или не участвовать» в ипотечном проекте.

Причем, необходимо учитывать что, в восприятии клиента оценка «тяжести» условий или привлекательности участия в ипотечном проекте происходит отнюдь не по логике строгих финансовых рассуждений, а в меру накопленной опытным путем культуры денежных расчетов. Современные условия таковы, что в рекламно-информационных предложениях часто указывают только привлекательную часть условий, не уделив должного внимания на обременяющие подробности, тем самым оставляя реалии предлагаемого бизнес-предложения далеко непрозрачными.

Наиболее вменяемая позиция тем не менее заключается в стремлении найти решение без ущемления по существу, интересов участников, не делая никого при этом «крайним». То есть сформировать оптимальную комбинацию параметров ипотечной схемы, находящуюся в согласии с ожиданиями всех участников, вот, пожалуй, единственно достойный выход, оставляющий внутренний мир авторов ипотечного проекта недеформированным.

Лекция 11

Измерение доходности

Доход – это денежные или иные ценности, получаемые в результате какой либо деятельности.

Доходность – способность приносить доход.

Перечислим виды возможных доходов при использовании финансовых инструментов:

1. Процентные деньги, взимаемые за предоставление ссуды.

2. Комиссионные, взимаемые за предоставление услуг.

3. Доходы от облигаций по купонам.

4. Доходы от курсовой разницы в стоимости ценных бумаг.

Степень финансовой эффективности (доходности) от различных по природе операций измеряется в виде ставки наращения чаще сложных, реже простых процентов.

Основная проблема при определении доходности финансовых и других операций заключается в разработке методик расчета условной годовой ставки наращения с учетом особенностей рассматриваемой финансовой операции.

Таким образом, такая условная ставка, как инструмент измерения доходности должна быть универсальной, то есть иметь одно общепринятое название, иметь общепринятые «единицы измерения». Однако, в финансовой литературе встречаются различные названия в зависимости от существующего на практике профиля финансовых операций. Так при рассмотрении простых депозитно-ссудных операциях эту роль играет эффективная ставка. В расчетах по оценке ценных бумаг, например облигаций, – полная доходность. При анализе инвестиций – внутренняя норма доходности. Что бы не путаться в терминах в качестве названия условной годовой ставки измерения доходности будем в дальнейшем рассмотрении будем употреблять термин «полная доходность».

Полная доходность – расчетная годовая ставка сложных процентов, при которой капитализация всех видов доходов от операции равна сумме инвестиций.

Иными словами начисление процентов по ставке полной доходности на вложения за рассматриваемый период времени обеспечивает выплату всех предусмотренных платежей. Соответственно, чем выше (больше значение) ставка доходности тем больше эффективность операции.

Значение ставки полной доходности определяется из уравнений эквивалентности финансового результата, от всех вложений полученного с использованием ставки полной доходности, финансовому результату финансовой операции для которой определяется ставка полной доходности.