Алгоритм наискорейшего спуска по дереву решений

Алгоритм рассмотрим на примере задачи о коммивояжере. Торговец должен побывать в каждом из 5 городов, обозначенных на карте.

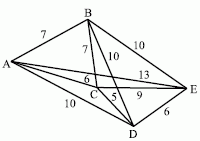
Задача состоит в том, чтобы, начиная с города А, найти минимальный путь, проходящий через все остальные города только один раз и приводящий обратно в А. Идея метода исключительно проста - из каждого города идем в ближайший, где мы еще не были.

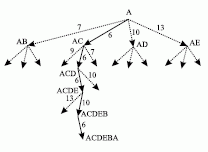
Такой алгоритм поиска решения получил название алгоритма наискорейшего спуска (в некоторых случаях - наискорейшего подъема).

Эвристический поиск.

Эвристический поиск – поиск в пространстве состояний, использующий некоторые знания, специфические для конкретной предметной области.

Простейшая форма эвристического поиска – это алгоритм под названием «восхождение на гору».

В процессе поиска в программе используется некоторая оценочная функция, с помощью которой можно грубо оценить, насколько "хорошим" или "плохим" является текущее состояние. Затем можно применить эту же функцию для выбора очередного шага, переводящего систему в следующее состояние.

Например, простая оценочная функция для программы игры в шахматы может включать очевидную оценку количества и качества имеющихся на доске фигур — своих и фигур соперника. Затем программа перебирает возможные операторы перехода в новое состояние (возможные ходы фигур) и, сравнивая результаты вариантов, отыскивает такой, который характеризуется максимальным значением оценочной функции. Другими словами, ищется такой ход, который дает наибольший материальный выигрыш.

Основной алгоритм, реализующий идею восхождения на гору, можно сформулировать следующим образом:

(1) Находясь в данной точке пространства состояний, применить правила порождения нового множества возможных решений, например множества ходов фигур, допустимых в данной позиции.

(2) Если одно из новых состояний является решением проблемы, прекратить процесс. В противном случае перейти в то состояние, которое характеризуется наивысшим значением оценочной функции. Вернуться к шагу (1).

Главная трудность применения алгоритма - формулирование оценочной функции, которая адекватно бы отражала "качество" текущего состояния.

Продолжая пример с игрой в шахматы, отметим, что иметь много фигур, больше чем у соперника, отнюдь не значит иметь лучшую позицию, т.е. быть ближе к успеху. Такая простая оценочная функция не учитывает многих особенностей игры.

Вторая трудность состоит в том, что на некотором этапе решения может оказаться так, что все возможные ходы одинаково хороши, в таком случае нет очевидного очередного хода. Этот случай представляет собой выход на "плато" в процессе восхождения, когда ни один из возможных путей не влечет за собой подъем.

Другой возможный источник затруднений — наличие локальных максимумов, из которых возможен только спуск, т.е. "ухудшение" состояния. Например, игрок 1 может взять ферзя игрока 2 и, несмотря на это, проиграть партию.

Преодолеть некоторые из рассмотренных трудностей можно путем применения другой формы эвристического поиска, которая получила наименование сначала наилучший или поиск «лучший — первый» (best-first search).

Поиск «лучший — первый» - это алгоритм поиска, который исследует граф путём расширения наиболее перспективных узлов, выбираемых в соответствии с указанным правилом.

В данном случае также имеется оценочная функция, с помощью которой можно сравнивать состояния в пространстве состояний.

Основное же отличие нового метода от ранее рассмотренного состоит в том, что сравниваются не только те состояния, в которые возможен переход из текущего, но и все, до которых можно "дотянуться".

Алгоритм поиска A* является примером оптимального поиска «лучший — первый».

Основная идея алгоритма состоит в использовании для каждого узла n на графе пространства состояний оценочной функции вида:

f(n)=g(n)+h(n).

Здесь g(n) соответствует расстоянию на графе от узла n до начального состояния, a h(n)— оценка расстояния от n до узла, представляющего конечное (целевое) состояние. Чем меньше значение оценочной функции f(n), тем "лучше", т.е. узел n лежит на более коротком пути от исходного состояния к целевому.

Идея алгоритма состоит в том, чтобы с помощью f(n) отыскать кратчайший путь на графе от исходного состояния к целевому.

Реализация Алгоритма А*.

Обозначения:

s — узел начального состояния;

g— узел целевого состояния;

OPEN — список, который содержит выбранные, но необработанные узлы;

CLOSED — список, который содержит обработанные узлы.

(1) OPEN:={s}.

(2) Если OPEN:={}, то прекратить выполнение. Пути к целевому состоянию на графе не существует.

(3) Удалить из списка OPEN узел n, для которого f(n) ≤ f(m) для любого узла m, уже присутствующего в списке OPEN, и перенести его в список CLOSED

(4) Сформировать список очередных узлов, в который возможен переход из узла n, и удалить из него все узлы, образующие петли; с каждым из оставшихся связать указатель на узел n.

(5) Если в сформированном списке очередных узлов присутствует g, то завершить выполнение. Сформировать результат — путь, порожденный прослеживанием указателей от узла g до узла s.

(6) В противном случае для каждого очередного узла n', включенного в список, выполнить следующую последовательность операций.

• Вычислить f(n').

• Если n' не присутствует ни в списке OPEN, ни в списке CLOSED, добавить его в список, присоединить к нему оценку f(n') и установить обратный указатель на узел n.

• Если n' уже присутствует в списке OPEN или в списке CLOSED, сравнить новое значение f(n)=new c прежним f(n')=old.

(7) Если old < new, прекратить обработку нового узла.

(8) Если new < old, заменить новым узлом прежний в списке, причем, если прежний узел был в списке CLOSED, перенести его в список OPEN.

(9) Конец алгоритма.