Количественная оценка риска актива (реального или финансового).

Рисковые активы характеризуются вероятностными значениями получения результата. Если известны все возможные значения результата (значения дохода в абсолютном выражении или относительное значение — доходность) и вероятности получения этих значений (сумма вероятностей равна единице), то такое представление результата носит название вероятностного распределения.

Вероятностное распределение может быть представлено в виде таблицы или графически. Например, если рассматривается владение недвижимостью (квартирой - назовем ее "актив А") и известны возможные цены продажи через год при различной ситуации в спросе (введение налога на недвижимость, ввод в эксплуатацию нового жилья и другие факторы могут повлиять на спрос), то вероятностное распределение может быть представлено в виде табл. 3.1.

Вероятностное распределение доходности вложения в актив А представим в виде диаграммы (рис. 3.2).

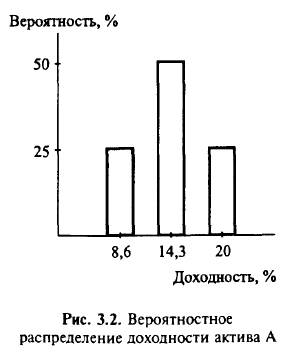
Ожидаемое значение результата определяется как сумма произведений возможных значений результата на соответствующие значения вероятности. Так ожидаемая доходность по инвестированию в недвижимость есть средневзвешенная величина возможных значений доходности: 20 х 0,25 + 14,3 х 0,5 + 8,6 х 0,25 = = 14,3%.

НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

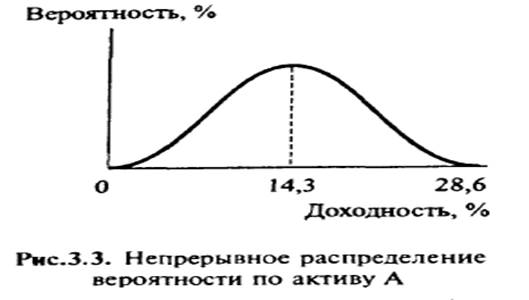
При предположении о возможности указать вероятность каждого исхода (в примере с активом А — указать вероятность его продажи по цене от 350 до 450 тыс. долл.) можно построить график непрерывного распределения вероятности (рис. 3.3).

В данном примере предполагается, что вероятность продать актив дешевле чем за 350 тыс. долл. и дороже чем за 450 тыс. равна нулю. Чем более заостренной будет форма кривой непрерывного распределения вероятности (плотнее распределение), тем больше вероятность, что фактическая доходность будет ближе к ожидаемому значению, и тем ниже риск принимаемого решения.

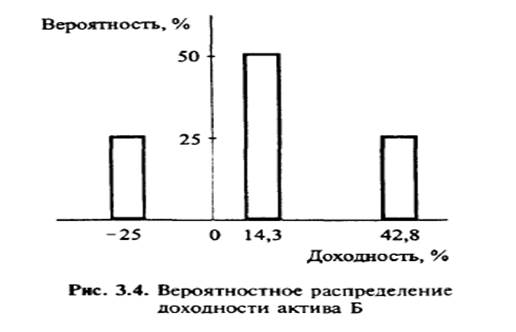
Например, инвестирование в нежилое помещение (создание и продажа офиса — актив Б) обеспечит вероятностное распределение доходности, представленное в табл. 3.2 и на рис. 3.4.

Такой вариант инвестирования более рискован, чем инвестирование в квартиру. При высоком спросе доходность может быть значительно выше (более чем в 2 раза), однако низкий спрос приведет к потере капитала

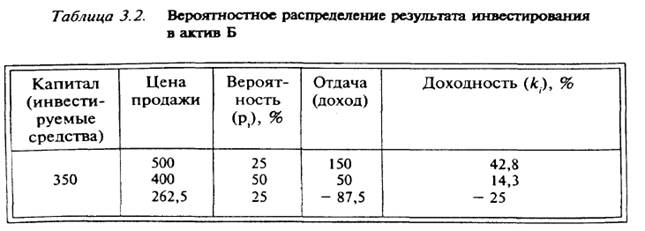
Непрерывное распределение вероятности по двум вариантам инвестирования представлено на рис. 3.5.

Первый вариант инвестирования характеризуется более заостренной формой кривой непрерывного распределения. Это означает, что фактическая доходность будет ближе к ожидаемому значению доходности 14,3%, чем по второму варианту, и, следовательно, первый вариант менее рискован.

НОРМАЛЬНОЕ ВЕРОЯТНОСТНОЕ РАСПРЕДЕЛЕНИЕ

Во многих исследованиях, включающих оценку вероятности, предполагается, что вероятностное распределение является нормальным.

Пример нормального распределения показан на рис. З.6а. Нормальное распределение симметрично относительно ожидаемого значения kож.

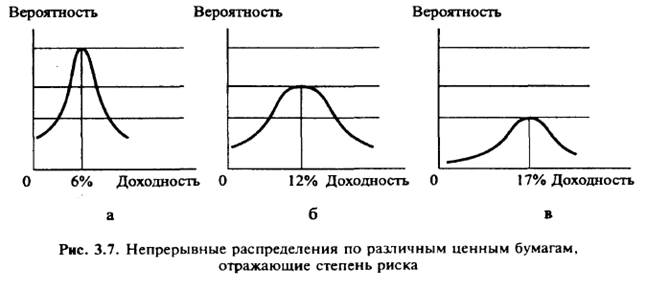
компаний: Распределение доходности по акциям молодых компаний гораздо сильнее скошено влево и характеризуется большой степенью разброса. Распределение доходности корпоративных облигаций можно считать нормальным (на длительных временных промежутках — логнормальным). По данным ежегодника Ибботсонского исследовательского центра построены непрерывные вероятностные распределения (рис. 3.7) для: а) корпоративных облигаций, б) акций стабильных компаний, в) акций молодых компаний.

МЕРА РИСКА

Для сравнения активов (реальных и финансовых) и принятия инвестиционных решений необходима количественная оценка риска, позволяющая ранжировать активы. В практике финансового менеджмента нашли применение несколько оценок риска:

1) дисперсия, как мера разброса возможных значений доходности;

2) стандартное отклонение, как мера разброса, выраженная в тех же единицах, что и результат (например, доходность);

3) коэффициент вариации для ранжирования активов с различными значениями ожидаемой доходности.

Мерой разброса возможных результатов вокруг ожидаемого значения является дисперсия (или вариация). Чем больше дисперсия, тем сильнее разброс.

Дисперсия дискретного распределения рассчитывается по формуле:

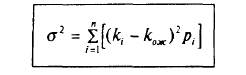
п — число возможных отклонений от ожидаемого значения.

Дисперсия доходности есть сумма произведений всех возможных отклонений фактических значений доходности от ожидаемого значения на вероятность этого отклонения. Дисперсия измеряется в тех же единицах, что и результат (в процентах, если в качестве результата рассматривается доходность, и в денежных единицах, если в качестве результата рассматриваются денежные потоки — выручка, издержки, прибыль и т.д.), но возведенных в квадрат.

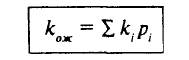
Для облегчения сравнения и анализа риска различных активов чаще используется квадратный корень из дисперсии — среднеквадратическое (или стандартное) отклонение:

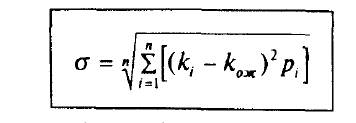
Стандартное отклонение более удобно, чем дисперсия, так как измеряется в тех же единицах, что и результат.

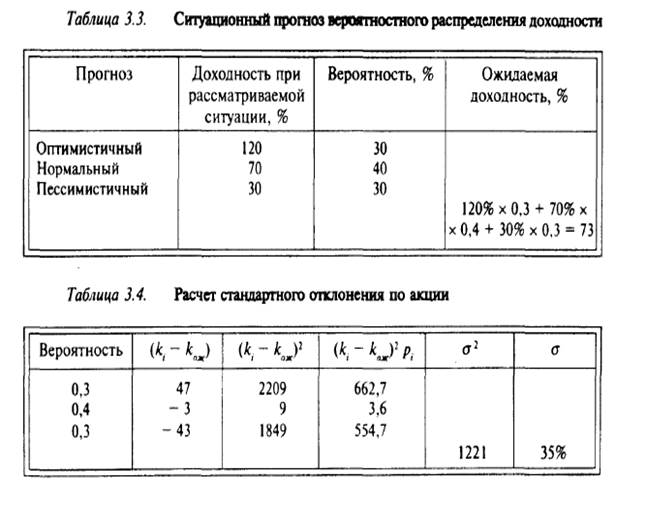
Рассмотрим возможные значения общей доходности по акциям АО "Красный Октябрь" (табл. 3.3). Прогноз строится на возможном изменении спроса на выпускаемую продукцию и макроэкономических факторов (экономический польем или спад).

Для оценки риска через стандартное отклонение необходимо: 1) рассчитать (расчет проведен в табл. 3.4) абсолютные отклонения возможных значений доходности от ожидаемого значения (ki - kож); 2) возвести в квадрат полученные отклонения (ki – kож)2; 3) домножить квадраты отклонений на соответствующее значение вероятности. Сумма произведений составит значение дисперсии σ2. Извлечем квадратный корень и получим значение стандартного отклонения σ.

Если сравниваются активы, имеющие различную доходность, то по значению стандартного отклонения нельзя сделать вывод, какой из них является более рискованным. Для сравнения активов с различной доходностью по степени риска необходимо уравнять разброс с учетом доходности, т.е. рассчитать риск на единицу доходности. Более рискованным будет тот актив, по которому выше риск на единицу доходности. Таким нормированным показателем степени риска является коэффициент вариации (СV), как отношение стандартного отклонения к ожидаемому значению результата:

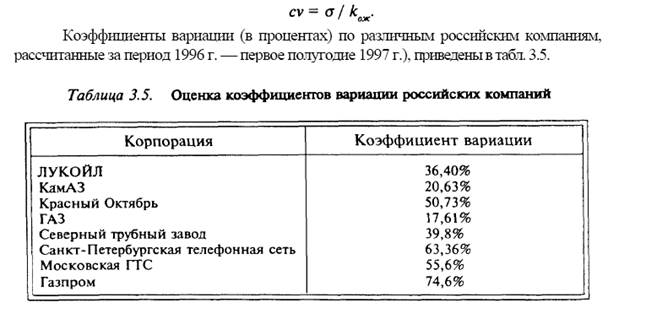
Чем выше коэффициент вариации, тем больше риск владения ценной бумагой. Такое утверждение верно при равной ликвидности рассматриваемых ценных бумаг.

Для понимания важности коэффициента вариации рассмотрим два актива А и Б, которые различаются ожидаемой доходностью и значением стандартного отклонения:

актив А актив Б

ожидаемая доходность 30% 10%

стандартное отклонение 4% 2%

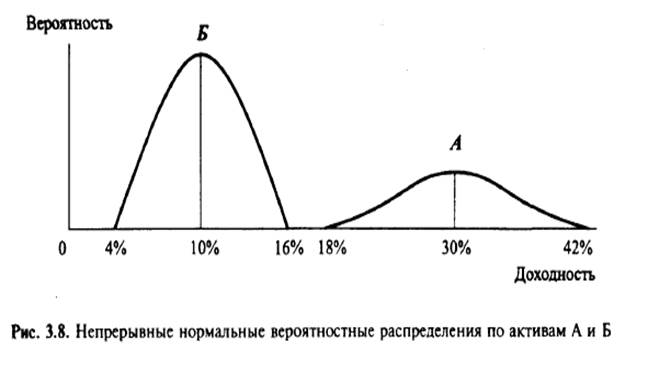
По более высокому значению стандартного отклонения актива А нельзя сделать вывод, что этот актив более рискован, чем актив Б. Расчет коэффициента вариации показывает, что СVA = 4/30 = 0,13, СVБ = 2/10 = 0,2, т.е. в действительности актив Б более рискован, чем А. Графический анализ подтверждает этот вывод. На рис. 3.8 показаны непрерывные нормальные вероятностные распределения по двум активам.

Актив Б характеризуется меньшим стандартным отклонением, и его вероятностное распределение более плотное. 99,7% результатов расположены в интервале {4%, 16%}, где 4% = kож - Зσ = 10% - 6% (см. табл. 3 Приложения 2).

Большинство значений результата (доходности) по активу А находится в интервале {18%, 42%}. Графическое представление показывает, что получение низких значений доходности более вероятно по активу Б, чем по активу А (самое низкое значение доходности по активу А находится на уровне 18%).