Полная доходность для простой учетной ставки с учетом комиссионных
Пусть вексель номиналом выдан на n лет с простой учетной ставкой d, причем при покупке векселя до срока (через k лет) удерживается комиссия Gk = S ´ (n – k) ´ g, где g комиссионный процент, который также может зависеть от срока покупки векселя.
 |
Рис.11.1
Стоимость векселя P к моменту его покупки через k лет после выпуска с учетом комиссии Gk будет равна
P = S ´ (1 – (n – k) ´ d) – Gk. (11.5)
Составим уравнение эквивалентности аналогично (11.1), то есть приравняем стоимость погашения векселя S, которую получит векселедержатель при погашении, стоимости покупки векселя P, наращенной по ставке полной доходности icэф за срок от покупки до погашения векселя (n – k) лет
(S ´ (1 – (n – k) ´ d) – Gk) ´ (1 + icэф)n = S. (11.6)
Из (11,6) легко найдется выражение для определения ставки полной доходности icэф
icэф = ((S ´ (1 – (n – k) ´ d) – S)/Gk)1/n – 1. (11.7)
В случае, если ставка учета векселя сложная dc выражение для определения ставки полной доходности icэф получается аналогичными рассуждениями.
Стоимость покупки векселя будет равна
P = S ´ (1 – dc)(n–k) – Gk. (11.8)
Уравнение эквивалентности принимает вид
(S ´ (1 – dc)(n–k) – Gk) ´ (1 + icэф)n = S. (11.9)
Значение ставки полной доходности определяется выражением
icэф = (S/(S ´ (1 – dc)(n–k) – Gk))1/n – 1. (11.10)
Доходность купли–продажи финансовых инструментов
Преследуя цели получения максимальных доходов или сохранения максимальной надежности вложений непрерывно приходится «перекладывать» и диверсифицировать инвестиции, то есть избавляться от мало доходных и ненадежных финансовых инструментов и приобретать другие, удовлетворяющие требованиям принятых решений относительно текущей рыночной коньюктуры.
Рассмотрим некоторые краткосрочные финансовые инструменты, существующие в деловом обороте для решения вышеупомянутых задач: вексель – долговое денежное обязательство, тратта – приказ одного лица уплатить по предъявлению тратты указанную сумму в указанные сроки, процентная тратта – тратта, которая предусматривает уплату процентных денег в зависимости от срока ее предъявления, депозитный сертификат – денежный документ, выпущенный под депонированные денежные средства (депонирование – сдача денежных средств на хранение).
Вексель
Рассмотрим вопрос полной доходности при покупке и последующей продажи векселя номиналом S. Его стоимость при покупке в момент t1 равна
P1 = S ´ (1 – d1 ´ (t0 – t1)/T0), (11.11)
где
d1 – простая учетная ставка при покупке;
T0 – срок на который выпущен вексель;
t0 – дата погашения векселя.
При продаже в момент времени t2 > t1 соответственно, стоимость векселя будет равна величине
P2 = S ´ (1 – d2 ´ (t0 – t2)/T0), (11.12)
где
d2 – значение той же учетной ставки, но уже при продаже.
Для нахождения величины простой ставки полной доходности iд запишем выражение, отражающее рост/уменьшение величины стоимости векселя от покупки P1 до стоимости продажи P2.
P2 = P1 ´ (1 + iд ´ (t2 – t1)/T), (11.13)
где
T – срок, на котором определена ставка полной доходности iд.
Из (11.13) получаем выражение для определения величины iд
iд = (P2/P1 – 1) ´ T/(t2 – t1). (11.14)
Очевидно, что при продаже возможно получение убытков (если курс учетной ставки d векселя снизился), что отразится на «знаке» ставки полной доходности, она станет отрицательной iд < 0.
В том случае, если требуется определить сложную ставку полной доходности icд выражение (11.13) будет иметь следующий вид
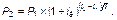 (11.15)
(11.15)
тогда выражение для определения сложной ставки полной доходности iсд будет выглядеть
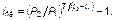 (11.16).
(11.16).
Облигации
Когда юридическому лицу необходимо занять очень большую сумму денег как правило невозможно найти какую-то одну финансовую компанию или даже небольшую группу финансовых компаний, которые смогли бы ссудить целиком необходимую сумму денег. Поэтому деньги должны быть получены от большого числа инвесторов как крупных, так и мелких. Для удобства обращения с большим числом инвесторов корпорация печатает заранее большое количество контрактов (ценных бумаг), в каждом из которых указана сумма займа, дата возмещения займа, норма процента, по которой будет возмещаться заем, и даты, когда эти процентные платежи будут делаться. В каждом контракте также устанавливается, где платежи могут быть собраны, и какие гарантии компания предлагает, чтобы заем был возмещен. Такой контракт называется облигацией.
Слово облигатный обозначает обязательный, непременный.
Облигация – вид ценной бумаги (долгового обязательства) по которой ее эмитент обязуется выплатить ее держателю фиксированную сумму денежных средств в определенный момент времени в будущем или выплатить доход, размер которого заранее установлен в форме определенного процента к номинальной стоимости облигации.
Облигации выпускаются для займа денег и, при этом, как правило, используются многочисленные средства для привлечения инвесторов. Для удобства обращения большинство облигаций выпускаются на предъявителя и могут передаваться от одного владельца другому по желанию. То есть облигация может быть продана владельцем в любой момент времени, когда он пожелает. Для гарантии выполнения обязательств по облигации, облигации могут быть именными, то есть по условиям обращения могут быть переданы только при соответствующем подтверждении и согласии выпустившей облигацию корпорации. Таким образом, владелец является защищенным от потерь или обмана. Для удобства получения процентов к большинству облигаций прилагаются купоны, которые можно обменять на наличные деньги в любом банке в указанную на купоне дату или позже.
Основные параметры облигации:
– номинальная цена – стоимость, указанная на бланке облигации;
– выкупная цена – цена, по которой эмитент готов/обязуется купить облигацию;
– купонная ставка или норма доходности облигации – процент от номинала выплачиваемый до срока погашения облигации;
– дата погашения облигации – дата, после которой эмитент обязуется выплатить предъявителю номинальную стоимость облигации;
– график дат выплат процентов по облигации – даты выплаты по купонам.
Поскольку львиная доля облигаций принадлежит не российскому рынку ценных бумаг, приведем некоторые характеристики из зарубежного опыта. Облигации могут подразделяться:
1) по методу обеспечения:
– государственные и муниципальные облигации имеют, как правило, государственную гарантию;
– облигации частных корпораций гарантированные активами предприятия;
– облигации частных корпораций без специального обеспечения;
2) по срокам погашения:
– облигации с фиксированной датой погашения;
– бессрочные облигации, без указания даты погашения;
3) по способу погашения номинала:
– погашение разовым платежом всего номинала;
– распределенное по времени погашение в долях от номинала;
– последовательное погашение – погашение некоторой части облигаций от общего числа облигаций;
4) по методу выплат дохода:
– выплата только процентов (купонов) по облигации (бессрочные облигации);
– облигации с нулевым купоном, т.е. без выплаты процентов по облигации;
– выплата купонов и номинала по окончанию срока облигации.
– периодические купонные выплаты и уплата номинала облигации в конце срока.
Рыночная цена облигаций при выпуске может быть равна, ниже (с дисконтом) или выше (с премией) номинала.
Существуют два вида рыночных цен:
– полная («грязная») цена, складывающаяся из цены облигации и процентов (купонных выплат) за период после последней выплаты процентов;
– чистая цена облигации – равная полной цене за вычетом сумм процентов (купонных выплат).
Расчет курса облигации определяется как отношение ее рыночной цены отнесенной к цене номинала и умноженной на сто:
Курс облигации = (рыночная цена/номинал) ´ 100.
Доходы облигаций это выплаты процентов по купонным выплатам, а также доход от разности между номиналом и ценой приобретения.
Количественный анализ облигаций состоит в определении следующих основных параметров:
– доходности облигаций;
– расчетов цены на произвольный момент времени;
– изменение динамики дисконта/премии по облигации.
