Табличный процессор Microsoft Excel
Лабораторная работа 1
Построение графиков функций и поверхностей
Цель работы:
знакомство с различными типами диаграмм и графиков;
приобретение навыков их построения;
освоить основные приемы редактирования и оформления диаграмм.
Диаграммы – удобное средство графического представления данных.На практике широко используется построение диаграмм средствами MS Excel. Они позволяют провести визуальный анализ данных в диапазоне, а также, при необходимости, выделяя из него отдельные ряды.
MS Excel поддерживает 15 типов стандартных и 20 типов нестандартных диаграмм. Создание диаграмм осуществляется с использованием «Мастера диаграмм» – программы, задающей вопросы, а затем использующая полученные ответы для создания диаграммы.
Рассмотрим работу «Мастера диаграмм» на двух примерах.
Пример 1
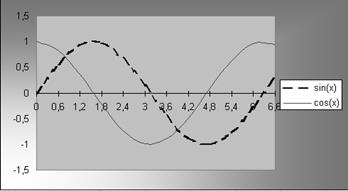
Построить графики функций у1(х)= sin(x) и y2(x) = cos(x) на интервале 0 до 6,6 с шагом 0,6.
Ход построения
1. На новом листе в первой строке сделать заголовок «Построение графиков функций».
2. В ячейках В4 и С4 сделать заголовки таблицы исходных данных: sin(x) и cos(x) для построения графиков.
3. Заполнить столбец значений аргумента х, начиная с ячейки А5: 0;0,6; ….; 6,6 (использовать автозаполнение).
4. В ячейку В5 записать формулу: = sin(А5) .
5. Скопировать эту формулу на остальные ячейки столбца до В16.
6. В ячейку С5 записать формулу: = cos (А5) .
7. Скопировать эту формулу на остальные ячейки столбца до С16.
| Построение графиков функций | ||
| sin(x) | cos(x) | |
| 0,6 | 0,564642 | 0,825336 |
| 1,2 | 0,932039 | 0,362358 |
| 1,8 | 0,973848 | -0,2272 |
| 2,4 | 0,675463 | -0,73739 |
| 0,14112 | -0,98999 | |
| 3,6 | -0,44252 | -0,89676 |
| 4,2 | -0,87158 | -0,49026 |
| 4,8 | -0,99616 | 0,087499 |
| 5,4 | -0,77276 | 0,634693 |
| -0,27942 | 0,96017 | |
| 6,6 | 0,311541 | 0,950233 |
8. Вызвать «Мастер диаграмм». Для этого щелкнуть по кнопке «Мастер диаграмм» на панели инструментов Стандартная или через меню «Вставка; Диаграмма».
a. Шаг 1: выбрать вкладку «Нестандартные», «гладкие графики», «далее».
b. Шаг 2: определить диапазон данных для построения А4:С16 с помощью мыши или вписать его в поле Мастера диаграмм с клавиатуры; «далее».
c. Шаг 3: заполнить параметры диаграммы.
d. Шаг 4: определить место размещения диаграммы.
9. Форматирование диаграммы.
При работе с диаграммой можно выделить:
– заголовок,
– легенду,
– область диаграммы,
– область построения диаграммы,
– ряды данных,
– подписи данных.
Любой элемент диаграммы можно форматировать. Для этого его прежде всего необходимо выделить. Затем при нажатии правой кнопки мыши появляется команда форматирования. В окнах этой команды отображаются все возможности изменения, индивидуальные для каждого элемента.
Для построенной диаграммы:
1. Выполнить заливку области построения диаграммы из нижнего левого угла.
2. Сделать ось ординат невидимой.
3. Изменить тип линии у синусоиды на пунктир.
4. Сохранить изменения.
Пример 2
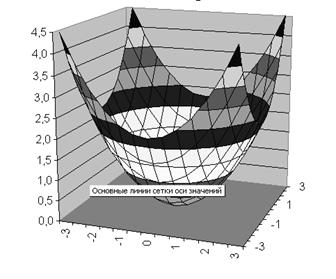
Построить поверхность эллиптического параболоида:
Z = x2/4 + y2/4 ,
Аргумент Х изменяется от (-3 ) до 3 с шагом 0,5. Аргумент У изменяется от (-3 ) до 3 с шагом 0,5.
Ход построения
1. Перейти на новый лист и в первой строке сделать заголовок «Построение поверхности».
2. Заполнить строку значений аргумента Y: начиная с ячейки В4 до ячейки N4.
3. Заполнить столбец значений аргумента Х, начиная с ячейки А5 до A17 .
4. В ячейку В5 записать формулу: = ($А5/2)^2 + (В$4/2) ^2 , закрепив четвертую строку и колонку А – диапазоны изменения аргументов.
5. Скопировать формулу на остальные ячейки диапазона В5: N17.
Диапазон построения поверхности:
| -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0,5 | 1,5 | 2,5 | |||||
| -3 | 4,5 | 3,8 | 3,3 | 2,8 | 2,5 | 2,3 | 2,3 | 2,3 | 2,5 | 2,8 | 3,3 | 3,8 | 4,5 |
| -2,5 | 3,8 | 3,1 | 2,6 | 2,1 | 1,8 | 1,6 | 1,6 | 1,6 | 1,8 | 2,1 | 2,6 | 3,1 | 3,8 |
| -2 | 3,3 | 2,6 | 2,0 | 1,6 | 1,3 | 1,1 | 1,0 | 1,1 | 1,3 | 1,6 | 2,0 | 2,6 | 3,3 |
| -1,5 | 2,8 | 2,1 | 1,6 | 1,1 | 0,8 | 0,6 | 0,6 | 0,6 | 0,8 | 1,1 | 1,6 | 2,1 | 2,8 |
| -1 | 2,5 | 1,8 | 1,3 | 0,8 | 0,5 | 0,3 | 0,3 | 0,3 | 0,5 | 0,8 | 1,3 | 1,8 | 2,5 |
| -0,5 | 2,3 | 1,6 | 1,1 | 0,6 | 0,3 | 0,1 | 0,1 | 0,1 | 0,3 | 0,6 | 1,1 | 1,6 | 2,3 |
| 2,3 | 1,6 | 1,0 | 0,6 | 0,3 | 0,1 | 0,0 | 0,1 | 0,3 | 0,6 | 1,0 | 1,6 | 2,3 | |
| 0,5 | 2,3 | 1,6 | 1,1 | 0,6 | 0,3 | 0,1 | 0,1 | 0,1 | 0,3 | 0,6 | 1,1 | 1,6 | 2,3 |
| 2,5 | 1,8 | 1,3 | 0,8 | 0,5 | 0,3 | 0,3 | 0,3 | 0,5 | 0,8 | 1,3 | 1,8 | 2,5 | |
| 1,5 | 2,8 | 2,1 | 1,6 | 1,1 | 0,8 | 0,6 | 0,6 | 0,6 | 0,8 | 1,1 | 1,6 | 2,1 | 2,8 |
| 3,3 | 2,6 | 2,0 | 1,6 | 1,3 | 1,1 | 1,0 | 1,1 | 1,3 | 1,6 | 2,0 | 2,6 | 3,3 | |
| 2,5 | 3,8 | 3,1 | 2,6 | 2,1 | 1,8 | 1,6 | 1,6 | 1,6 | 1,8 | 2,1 | 2,6 | 3,1 | 3,8 |
| 4,5 | 3,8 | 3,3 | 2,8 | 2,5 | 2,3 | 2,3 | 2,3 | 2,5 | 2,8 | 3,3 | 3,8 | 4,5 |
6. Мастер диаграмм.
7. Выбрать тип «Стандартный», «Поверхность»
8. Выполнить все этапы построения диаграммы.
Варианты графиков
1. y(х) = 10x2+2x+c, x = -5, -4, .... , 4, 5; при разных с (c = -2; 10).
2. y(х) = 5*sin(kx), x = -5, -4, .... , 4, 5; при разных k (k = -1;4).
3. y(х) = a3/(a2+x2), x = -5, -4, .... , 4, 5; при разных а (а = -1; 3).
4. y(х) = ex sin(kx), x = 0, 0,8, 1,6, ... , 12 при разных k (k = 2; 6);
5. y(х) = a x3 e-x, x = 0, 0,2,...., 1,8, 2 при разных а (а = -2; 4).
6. y(х) = 2*exp(-x+cx2), x = 0, 0,5, … 5,5, 6 при разных с (c = -2; 0,1).
7. y(х) = 3x3+bx2+4x-12, x = -5, -4, .... , 9, 10 при разных b (b = 0,4; 5).
8. y(х) = sin(Kx)/x, x = 0,l, 0,6, ...., 10,1 при разных k (k =-1; 2).
9. y(х) = Ln(х+π/х2+a), х = -10, -9.5, … 10 при разных а (а=2; 0,5).
10. y(х) = aLn((х+1)/(х-1)), х = 1,1, 1,2, … , 6 при разных а (а = 0,5; 2).
11. y(х) = 3x3-bx+12, x = 1,5, 3, 4,5, ...., 10,5 при разных b (b = 0,4; 5).
Построение поверхностей
1. z(х,у) = 4х /5y2, х = [-5; 5] шаг 0,5; у = [0,1; 1,1] шаг 0,05.
2. z(х,у) = х3 + 3ху2-5х-4у,............. х = [-5; 5] шаг 0,5; у =[-5; 5] шаг 0,5.
3. z(х,у) = 2x2-2xy+3y2+x-y,........... x=[-5; 5] шаг 0,5; у =[-5; 5] шаг 0,5.
4. z(х,у) = sin х+ sin(х+у),............. х =[0;4] шаг 0,2; у = [0; 4] шаг 0,2.
5. z(х,у) = ехр(х/2)*(х+у2),........ х =[-5; 5] шаг 0,5; у = [-5; 5] шаг 0,5.
6. z(х,у) = (sin х+sin у)*ln (10+х), х =[0;4] шаг 0,2; у = [0; 4] шаг 0,2.
7. z(х,у) = 0,5sin(х2+у2),................ х =[ 0; 2] шаг 0,1 ; у = [0; 2] шаг 0,1.
8. z(х,у) = 2*Ln (3ху+1,2),............ х =[-2; 2] шаг 0,2; у = [-2; 2] шаг 0,2.
9. z(х,у) = x4 + y4-2x2-4xy-y2, ......... х =[-2; 2] шаг 0,2; у = [-2; 2] шаг 0,2.
10. z(х,у) = x3+3y3-6xy+l, х =[-5; 5] шаг 0,5; у = [-5; 5] шаг 0,5.
11. z(х,у) = sinх * siny+(x+y)2, х =[-2;2] шаг 0,2; у = [-2; 2] шаг 0,2.
Лабораторная работа 2
Действия с матрицами и определителями
Цель работы:
знакомство с особенностями функций рабочего листа Microsoft Excel, предназначенными для работы с матрицами;
приобретение навыков практического использования этих функций;
нахождение приближенного решения систем линейных уравнений.
Mirosoft Excel предоставляет несколько функций для выполнения операций с матрицами. Эти функции находятся в категории «Математическая». Рассмотрим примеры использования.
Пример 1
Даны матрицы две А и В, матрица А – квадратная. Выполнить операции с матрицами:
1. Транспонировать матрицу А.
2. Найти матрицу, обратную А.
3. Вычислить произведение матриц А и В.
4. Вычислить произведение матрицы А и обратной к ней.
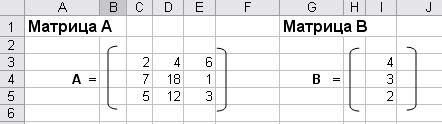
Ввести матрицы А и В.
 |
1. Транспонирование матрицы А:
1. Выделить ее (например, диапазон ячеек С3 : Е5).
2. Скопировать выделенный фрагмент в буфер обмена.
3. Перейти в ячейку, где должен разместиться левый верхний элемент транспонированной матрицы.
4. Выбрать команду «Специальная вставка» меню Правка.
5. В открывшемся диалоговом окне активизировать флажок «транспонировать».
6. Щелкнуть на кнопке ОК.
Эту же операцию можно выполнить с помощью функции ТРАНСП из категории «Математические».
В примере получим:
| Транспонированная Аt | |||||
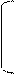 |  | ||||
| Аt= | |||||
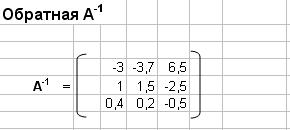
2. Вычисление обратной матрицы А-1
1. Выбрать функцию МОБР из категории «Математические» .
2. В поле ввода «Массив» указать исходный диапазон (например, диапазон ячеек С3 : Е5), ОК.
3. Выделить диапазон ячеек, где должны появиться элементы обратной матрицы (например, С24 : Е26), причем первая ячейка диапазона должна содержать функцию = МОБР(С3 : Е5);
4. Нажать F2;
5. Закончить ввод формулы массива нажатием клавиш (CTRL;SHIFT)+ENTER (первые две вместе, затем третья).
В примере получим:
 |
3. Вычисление произведения матриц А и В
1. Выбрать функцию МУМНОЖ() из категории «Математические».
2. В поле ввода «Массив» указать первый исходный диапазон (например, диапазон ячеек С3 : Е5) и второй исходный диапазон (например, диапазон ячеек I3 : I5).
3. Выделить диапазон ячеек, где должны появиться элементы матрицы произведения (например, I10 : I13), причем первая ячейка диапазона должна содержать функцию =МУМНОЖ (С3 : Е5; I3 : I5).
4. Нажать F2.
5. Закончить ввод формулы массива нажатием клавиш (CTRL;SHIFT)+ENTER (первые две вместе, затем третья).
6. В примере получим:
 |  | |||
| A х B = | ||||
Замечание. Умножать можно только согласованные матрицы.
4. Вычислить произведение матрицы А и обратной к ней
Для получения этого произведения необходимо умножить матрицы А и А-1, полученную в пункте 2 .
В результате выполнения этой операции получим единичную матрицу того же порядка.
Пример 2
Дана система линейных уравнений. Найти её решение с точностью до одного знака после запятой методом Крамера.
Выполнить проверку полученного решения системы уравнений.
Решить систему линейных уравнений третьего порядка:
1х + 2у – 3z = 5
2х + 4z = 2
1х + 4у = 9
Ход выполнения
1. Ввести коэффициенты системы и правую часть уравнений, как это показано на рисунке:
| Коэффициенты | Правая часть | ||||
| х | у | z | |||
| –3 | |||||
2. Используя функцию МОПРЕД( … )для нахождения определителя, вычислить определитель системы Δ.
В предложенном примере Δ = -32, 0
Последовательно заменяя столбцы коэффициентов при неизвестных на вектор правой части вычислить определители Δx, Δy, Δz.
Они равны соответственно: Δx = -32,0 ;
Δy = -64,0;
Δz = 0 .
Отсюда вытекает: х = Δx / Δ = -32,0/(-32,0) = 1,0;
y = Δy / Δ = -64,0/(-32,0) = 2,0;
z = Δz / Δ = -0/(-32,0) = 0.
Для проверки подставляем полученные значения неизвестных в уравнения системы:
1 · 1.0 + 2 · 2.0 – 3 · 0 = 5
2 · 1.0 + 4 · 0 = 2
1.0 + 4 · 2.0 = 9
Полученные числовые значения правых частей уравнения совпадают с исходными значениями. Проверка показала правильность найденного решения системы.
Варианты заданий
Матрицы
1.
| А= | 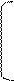 | 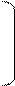 | В = |  | 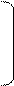 21 21 | ||||||
2.
| А= | 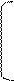 | 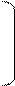 | В = |  | 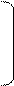 2 2 | ||||||
3.
| А= | 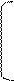 | 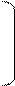 | В = |  | 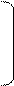 2 2 | ||||||
4.
| А= | 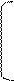 |  | В = |  |  2 2 | ||||||
5.
| А= |  |  | В = |  | 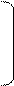 1 1 | ||||||
6.
| А= | 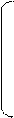 | 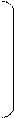 | В = | 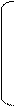 |  12 12 | |||||||
7.
| А= | 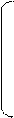 | 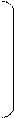 | В = | 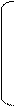 |  9 9 | |||||||
8.
| А= | 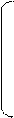 | 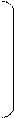 | В = | 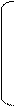 |  8 8 | |||||||
9.
| А= | 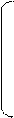 | 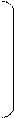 | В = | 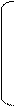 |  13 13 | |||||||
10.
| А= | 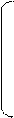 | 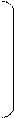 | В = | 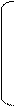 |  14 14 | |||||||
