Фактор времени

Если бы кривая доходности имела постоянный уровень и рыночные процентные ставки оставались неизменными, цена на любые безрисковые дисконтные облигации течением времени непрерывно повышалась бы, а цена на любые премиальные — снижалась. Связано это с тем, что с течением времени дата погашения облигаций приближается, а на момент погашения их цена должна равняться номинальной стоимости. Таким образом, по мере приближения даты погашения, цена на дисконтные и премиальные облигации будет стремиться к своему номиналу. На рис. 8.3 приведена динамика цен на бескупонные дисконтные облигации со сроком погашения 20 лет.

Рассмотрим метод расчета цены облигации, принимая во внимание, что номинальная стоимость облигации равна 1000 долл., а доходность остается фиксированной на уровне 6% в год. Первоначально облигация имеет срок погашения 20 лет и ее цена составляет:

n	i	PV	FV	РМГ	Результат
	6%	?			РV=311,80долл

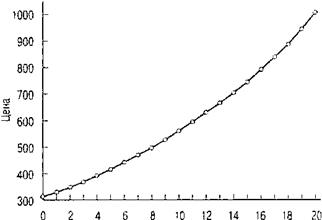
Время от даты выпуска облигации (лет)

Рис. 8.3. Динамика роста цены бескупонной облигации

Примечание: С течением времени при неизменной процентной ставке и равномерной структуре платежей цена бескупонной облигации будет расти со скоростью, эквивалентной ее доходности при погашении. График составлен из расчета номинала облигации 1000 долл. и 6% годовой доходности.

По истечении одного года со времени выпуска облигации до окончания ее срока погашения останется 19 лет и цена будет равна:

n	i	PV	FV	РМГ	Результат
	6%	?			PV= 330,51	долл.

Таким образом, величина пропорционального изменения цены облигации точно соответствует ее доходности (6% в год):

Пропорциональное изменение цены = (330,51 долл. – 331,80 долл.) / 311,80 долл. = 6%

Вопрос 8.5

Какой будет цена бескупонной облигации через два года, если доходность зафиксируется на уровне 6% в год? Удостоверьтесь, что величина пропорционального изменения цены за второй год составит 6%.