Процесс дисконтирования инвестиций методом простого процента
Процесс наращения инвестиций методом простого процента
Под наращенной суммой ссуды (долга, депозита, других видов инвестированных средств) понимается первоначальная ее сумма вместе с начисленными на нее процентами к концу срока.
Пусть P первоначальная сумма денег, i - ставка простых процентов. Начисленные проценты за один период равны Pi, а за n периодов - Pni.
Процесс изменения суммы долга с начисленными простыми процентами описывается арифметической прогрессией, членами которой являются величины
P, P+Pi=P(1+i), P(1+i)+Pi=P(1+2i)и т.д. до P(1+ni).
Первый член этой прогрессии равен P, разность Pi, а последний член определяемый как
S=P(1+ni) (1)
и является наращенной суммой. Формула (1) называется формулой наращения по простым процентам или, кратко, формулой простых процентов. Множитель (1+ni) является множителем наращения. Он показывает во сколько раз наращенная сумма больше первоначальной суммы. Наращенную сумму можно представить в виде двух слагаемых: первоначальной суммы P и суммы процентов I
S=P+I, (2)
где
I=Pni. (3)
Процесс роста суммы долга по простым процентам легко представить графически (см. Рис. 1). При начислении простых процентов по ставке i за базу берется первоначальная сумма долга. Наращенная сумма S растет линейно от времени.
рис.1
Процесс дисконтирования инвестиций методом простого процента
При заключении финансовых соглашений часто приходится решать задачу, обратную задаче нахождения наращенной суммы. Например, по заданной сумме F, которую предполагают получить (или уплатить) через время , требуется определить величину капитала Р, который необходимо инвестировать в данный момент, чтобы через время при постоянной процентной ставке получить сумму F. Аналогичная задача (нахождение Р по F) возникает и в том случае, когда проценты удерживаются непосредственно при выдаче ссуды (Р).
Как уже упоминалось, такое движение денежных средств от будущего к настоящему носит название дисконтирования. Говорят, что капитал F дисконтируется (или учитывается); величина удержанных процентов часто называется дисконтом (discount). Заметим, кстати, что так же иногда называют и учетную ставку. Капитал Р, найденный с помощью процесса дисконтирования суммы F, в зависимости от контекста называется приведенной (современной, текущей, капитализированной) стоимостью. Понятие приведенной стоимости является одним из важнейших в количественном анализе финансовых операций.
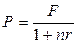
Рассмотрим вначале математическое дисконтирование, являющееся процессом, обратным наращению первоначального капитала. При математическом дисконтировании решается задача нахождения такой величины капитала Р, которая через лет при наращении по простым процентам по ставке будет равна F. Решая (2.1) относительно Р, получим:
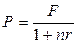(2.15)
Таким образом, величина Р является приведенной стоимостью величины F. Дисконт-фактор (дисконтный множитель)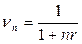 
показывает долю капитала Р в F. Дисконтный множитель также называется коэффициентом дисконтирования и представляет собой величину, обратную множителю наращения простых процентов в (2.1). В качестве ставки дисконтирования используется процентная ставка . Разность между F и Р называется дисконтом:
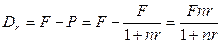(2.16)
В дореволюционной российской практике величину D,называли также учетом или математическим учетом.
Формула (2.16) представляет собой вычисление процентов "на 100" величины F, следовательно, такими процентами по формуле (2.15) учитывается капитал F=1,n=1. Дис= формулы (2.16) следует, что
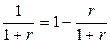
Таким образом, если в качестве денежной единицы рассматривать, например, рубль, то дисконтный множитель представляет собой разность между рублем и его процентами за один год "на 100".