Основные теоретические положения. Рассмотрим задачу планирования производства на примере балансовой модели.

Рассмотрим задачу планирования производства на примере балансовой модели.

Экономическая система состоит из трех отраслей. Объемы производства каждой из отраслей за предыдущий период, текущее производственное потребление в отраслях, а также прогнозируемый конечный спрос продукции каждой из трех отраслей приведены в табл. 8. Определить конечную продукцию каждой из отраслей за предыдущий период и план выпуска продукции в следующем периоде, считая, что технология производства не изменилась.

Таблица 8

Отрасли	Объемы производства отраслей	Производственное потребление отраслей за предыдущий период	Прогнозируе-мый конечный спрос

Математическая постановка задачи

Для решения поставленной задачи можно использовать балансовую модель Леонтьева. Она представляет собой систему уравнений, каждое из которых выражает требование равенства (баланса) между количеством продукции, производимой отдельным экономическим объектом, и совокупной потребностью в этой продукции. В рассматриваемой задаче экономическая система состоит из трех отраслей.

Пусть Х_i – величина, равная суммарному выпуску продукции отрасли i;

x_ij – количество продукции отрасли i, необходимое для того, чтобы отрасль jпроизвела X_j единиц своей продукции;

Y_i – количество продукции отрасли i, оставшееся для внешнего потребления (конечная продукция).

Тогда взаимосвязь отраслей в процессе производства и потребления отдельного продукта Х_i (i=1, 2, 3) может быть описана в виде следующих уравнений:

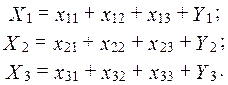(1)

Используем понятие коэффициентов прямых затрат (технологических коэффициентов) a_ij:

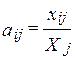– количество продукции отрасли i, необходимое для того, чтобы отрасль j произвела одну единицу своей продукции.

Тогда x_{i j} = a_ijX_j и система уравнений (7) будет иметь следующий вид:

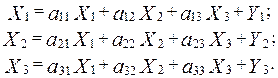(2)

Или в матричной форме

Х=АХ+Y, (3)

где 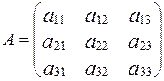– матрица прямых затрат,

Х – вектор-столбец выпуска продукции в предыдущем периоде.

Y– вектор-столбец конечного спроса в предыдущем периоде.

Решение задачи

2.2.1. Определение вектора конечной продукции за предыдущий период

По условию задачи известны объемы производства каждой из отраслей за предыдущий период (суммарный выпуск продукции отрасли i): X₁ = 600, X₂ = 1000, X₃ = 800 и значения x_ij (i, j = 1, 2, 3):

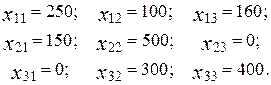
Отсюда, используя (1), можно определить значения Y_i , i = 1, 2, 3, конечной продукции каждой из отраслей за предыдущий период.

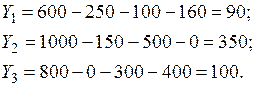(4)

Таким образом, вектор конечной продукции за предыдущий период найден Y = (90, 350, 100).

Для определения вектора выпуска продукции Хпри заданном конечном прогнозируемом векторе спроса Y = (2000, 2000, 3000) надо решить систему уравнений (3), из которого следует, что

Х = (Е-А)^-1Y, (5)

где Е – единичная матрица.

Матрица S=(E-A)^-1 – называется матрицей полных затрат.

2.2.2. Определение коэффициентов прямых затрат

Учитывая, что технология производства не изменилась, определим коэффициенты прямых затрат a_ij:

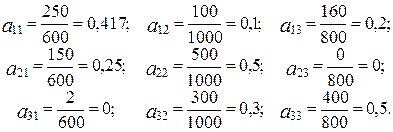
Таким образом, матрица коэффициентов прямых затрат будет иметь вид

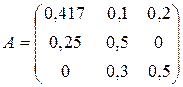. (6)

2.2.3. Проверка продуктивности матрицы

Все элементы матрицы А неотрицательные, А³ 0.

Для того чтобы система уравнений (5) имела единственное неотрицательное решение при любом неотрицательном векторе Y, необходимо, чтобы матрица А была продуктивной. Экономический смысл продуктивности состоит в том, что существует такой план выпуска продукции, при котором каждая отрасль сможет произвести необходимое количество конечной продукции. Можно показать, что для продуктивности матрицы А необходимо и достаточно, чтобы все главные миноры матрицы (Е-А) были положительными числами строго меньше единицы. Кроме того, известно: если сумма элементов каждого из столбцов неотрицательной квадратной матрицы А положительна и строго меньше единицы, то все главные миноры матрицы (Е-А) положительны и строго меньше единицы.

Суммы элементов каждого столбца матрицы А (6) соответственно равны:

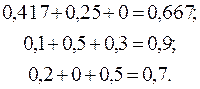
Следовательно, в силу вышесказанного, матрица А продуктивна, выражение (5) имеет смысл и вектор Y неотрицателен. Следовательно, для нахождения плана выпуска продукции Х можно воспользоваться формулой (5).

2.2.4. Вычисление матрицы Е - А

Вычислим матрицу (Е - А):

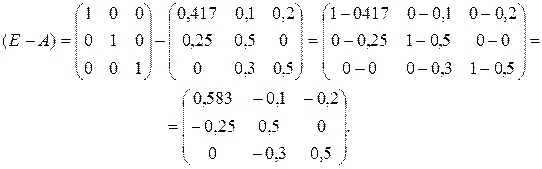(7)

2.2.5. Вычисление обратной матрицы (Е-А)^-1

Известно, что матрица В^-1 называется обратной по отношению к квадратной матрице В, если произведение В * В^-1 = Е (Е – единичная матрица).

Для вычисления обратной матрицы воспользуемся формулой:

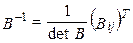. (8)

Здесь (B_ij) – матрица, полученная из элементов B_ij, а B_ij – алгебраические дополнения элементов матрицы.

B_ij=(-1)^i+j M_ij, (9)

где M_ij – минор элемента a_ij (минор – это такой определитель, который получается из матрицы вычеркиванием строки и столбца, на пересечении которых стоит данный элемент).

Вычислим значения алгебраических дополнений элементов матрицы (Е - А). Обозначим для простоты вычислений Е -А=В

; ;

; ;

; ;

; ;

.

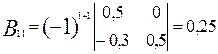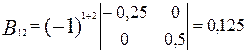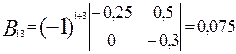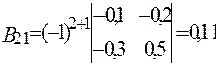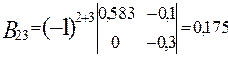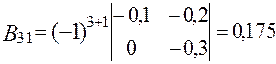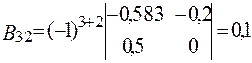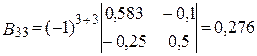Таким образом, .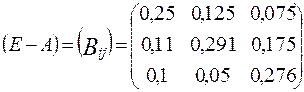

2.2.6. Вычисление транспонированной матрицы

Поменяв в матрице [Е-А] строки и столбцы местами, получаем

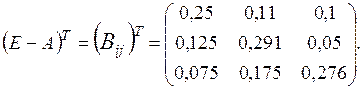
2.2.7. Вычисление определителя матрицы [Е-А]

Вычислим определитель, применив разложение по первой строке

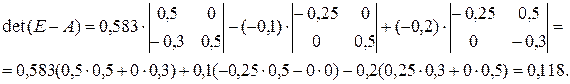
2.2.8. Вычисление матрицы прямых затрат S

По формуле S=(E-A)^-1=B^-1=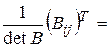

.

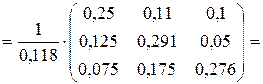
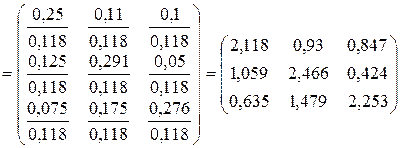2.2.9. Определение вектора выпуска продукции Х

Зная S и Y, вычислим Xпо формуле:

Х=S×Y .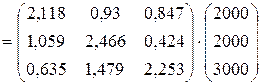

Отсюда

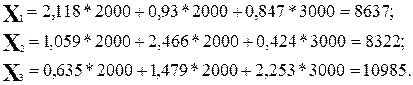
Таким образом, вектор выпуска продукции в следующем периоде при заданном векторе конечной продукции Y = (2000, 2000, 3000) равен

X = (8637, 8322, 10985).

Очевидно, что с использованием матричных операций в электронных таблицах процедура вычислений в балансовой модели существенно упрощается.

Порядок выполнения работы

Задание. Реализовать балансовую модель в электронной таблице (ЭТ).

Выполнение задания

Компьютерная реализация балансовой модели в ЭТ показана в табл. 9 (режим показа формул в Excel), табл. 10 (режим показа формул в Calc) и в табл. 11 (режим показа вычислений).

Для реализации задачи в электронной таблице выполним следующие действия:

3.1.1. Создать блок исходных данных. В ячейки А2:D5 ввести исходные данные из таблицы задания.

3.1.2. В ячейках B6:D8 разместить формулы для вычисления технологических коэффициентов:

· в ячейку В6 ввести формулу для вычисления первого коэффициента =B3/A$3 и скопировать ее в ячейки В7:B8;

Таблица 9. Балансовая модель. Показ формул в Excel

	A	B	C	D
	БАЛАНСОВАЯ МОДЕЛЬ
	Объём про- изводства	Потребление отраслей
	Вычисление технологиче-ских коэф-фициентов	=В3/А$3	=С3/А$4	=D3/А$5
	= В4/А$3	=С4/А$4	=D4/А$5
	= В5/А$3	=С5/А$4	=D5/А$5
	Проверка продуктивности матрицы А
		=СУММ(B6:B8)	=СУММ(C6:C8)	=СУММ(D6:D8)
	=ИЛИ(B10>=1;C10>=1;D10>=1)	=ЕСЛИ(A11=ИСТИНА;"Решения нет";"Матрица продуктивна")
	Единичная матрица
	Вычисление Е-А	=B12-B6	=C12-C6	=D12-D6
	=B13-B7	=C13-C7	=D13-D7
	=B14-B8	=C14-C8	=D14-D8
	Вычисление обратной матрицы	=МОБР(B15:D17)	=МОБР(B15:D17)	=МОБР(B15:D17)
	=МОБР(B15:D17)	=МОБР(B15:D17)	=МОБР(B15:D17)
	=МОБР(B15:D17)	=МОБР(B15:D17)	=МОБР(B15:D17)
	Спрос на будущий период		План выпуска продукции	=МУМНОЖ(B18:D20;B21:B23)
		=МУМНОЖ(B18:D20;B21:B23)
		=МУМНОЖ(B18:D20;B21:B23)

· аналогично в ячейку С6 ввести формулу =C3/A$4 и скопировать ее в ячейки С7:С8;

· в ячейку D6 ввести формулу =D3/A$5 и скопировать ее в ячейки D7:D8.

3.1.3. В ячейках В10:D10 разместить формулы для подсчета суммы значений элементов по столбцам:

· в ячейку В10 ввести формулу =СУММ(В6:В8) (В программе OpenOffice.org Calc вводим формулу =SUM(В6:В8));

· скопировать формулу в ячейки С10:D10.

3.1.4. В строке 11 размещаем формулы для проверки продуктивности матрицы технологических коэффициентов:

Таблица 10. Балансовая модель. Показ формул в Calc

	A	B	C	D
	БАЛАНСОВАЯ МОДЕЛЬ
	Объём про- изводства	Потребление отраслей
	Вычисление технологиче-ских коэф-фициентов	=В3/А$3	=С3/А$4	=D3/А$5
	= В4/А$3	=С4/А$4	=D4/А$5
	= В5/А$3	=С5/А$4	=D5/А$5
	Проверка продуктивности матрицы А
		=SUM(B6:B8)	= SUM (C6:C8)	= SUM (D6:D8)
	=OR(B10>=1;C10>=1;D10>=1)	=IF(A11=ИСТИНА;"Решения нет";"Матрица продуктивна")
	Единичная матрица
	Вычисление Е-А	=B12-B6	=C12-C6	=D12-D6
	=B13-B7	=C13-C7	=D13-D7
	=B14-B8	=C14-C8	=D14-D8
	Вычисление обратной матрицы	=MINVERSE(B15:D17)	= MINVERSE (B15:D17)	= MINVERSE (B15:D17)
	= MINVERSE (B15:D17)	= MINVERSE (B15:D17)	= MINVERSE (B15:D17)
	= MINVERSE (B15:D17)	= MINVERSE (B15:D17)	= MINVERSE (B15:D17)
	Спрос на будущий период		План выпуска продукции	=MMULT(B18:D20;B21:B23)
		= MMULT (B18:D20;B21:B23)
		= MMULT (B18:D20;B21:B23)

· в ячейку А11 ввести формулу =ИЛИ(В10>=1;C10>=1;D10>=1) (В OpenOffice.org Calc вводим формулу =OR(B10>=1;C10>=1;D10>=1).

Эта формула проверяет содержимое ячеек В10:D10. Если хотя бы в одной из этих ячеек значение больше единицы (т.е. сумма значений элементов хотя бы в одном столбце превышает единицу), то в ячейке А11 будет записано значение ИСТИНА». В противном случае – значение «ЛОЖЬ»;

· в ячейку C11 ввести формулу

=ЕСЛИ(А11=”ИСТИНА”;”Нет решения”;”Матрица продуктивна”).

В программе OpenOffice.org Calc вводим формулу

=IF(A11=”ИСТИНА”;”Нет решения”;”Матрица продуктивна”).

Эта формула проверяет содержимое ячейки А11 и если сумма элементов хотя бы одного столбца превысила единицу, выводит сообщение “Нет решения”, а в противном случае – “Матрица продуктивна”.

3.1.5. В строках 12 –14 разместить единичную матрицу Е.

3.1.6. В строках 15 – 17 произвести вычисление матрицы Е-А:

· в ячейку В15 поместить формулу =В12-В6;

· скопировать формулу в ячейки В16:D17.

3.1.7. В строках 18 – 20 разместим формулы для вычисления матрицы, обратной матрице Е-А:

· активизировать ячейку В18;

· зажав левую клавишу мыши, выделить диапазон ячеек В18:D20, где будет размещена обратная матрица;

· щелкнуть по пиктограмме Мастер функций f_x;

· в первом окне Мастера функций в поле Категория выбрать Математические(В программе OpenOffice.org Calcв поле Категория выбрать Массив);

· в поле Функциясреди расположенных по алфавиту функций найти функцию МОБР(В программе OpenOffice.org Calcфункцию MINVERSE);

· щелкнуть по кнопке Ок (Далее) и перейти во второе окно Мастера функций;

· в поле Массив (Матрица) ввести адрес матрицы Е-А: диапазон ячеек В15:D17;

· чтобы формула была введена во все ячейки выделенного диапазона, следует одновременно нажать клавиши Ctrl+Shift+Enter; после этого в ячейки В18:D20 будет введена формула =МОБР(В15:D17) (В программе OpenOffice.org Calc – формула =MINVERSE(В15:D17)).

3.1.8. В строках 21 – 23 поместим формулы для вычисления плана выпуска продукции:

· в ячейках В21:В23 разместить значения спроса на будущий период согласно заданию (табл. 8);

· выделить ячейки D21:D23, в которых будет размещена формула перемножения элементов матрицы, обратной Е-А, и вектора-столбца спроса;

· выполнить команды Вставка – Функция;

· в категории Математические (в ЭТ Calc - Массив) Мастера функцийвыбрать функцию МУМНОЖ(в ЭТ Calc - MMULT);

· во втором окне Мастера в поле Массив1 (матрица) ввести адрес обратной матрицы: диапазон ячеек В18:D20;

Таблица 11. Балансовая модель. Показ вычислений

	A	B	C	D
	БАЛАНСОВАЯ МОДЕЛЬ
	Объём производства	Потребление отраслей
	Вычисление технологических коэффициентов	0,417	0,1	0,2
	0,25	0,5
		0,3	0,5
	Проверка продуктивности матрицы А
		0,667	0,900	0,700
	ЛОЖЬ	Матрица продуктивна
	Единичная матрица
	Вычисление Е-А	0,583	-0,1	-0,2
	-0,25	0,5
		-0,3	0,5
	Вычисление обратной матрицы	2,113	0,930	0,845
	1,056	2,465	0,423
	0,634	1,479	2,254
	Спрос на будущий период		План выпуска продукции	8619,72
		8309,86
		10985,92

· в поле Массив2 (в ЭТ Calc - Матрица) ввести адрес вектора-столбца спроса: диапазон ячеек В21:В23;

· чтобы формула была введена во все ячейки выделенного диапазона, следует одновременно нажать клавиши Ctrl+Shift+Enter. После этого в ячейки D21:D23 будет введена формула =МУМНОЖ(В18:D20;B21:B23) (В программе OpenOffice.org Calc – формула =MMULT(В18:D20;В21:В23)).

Самостоятельная работа

Приведите расчеты балансовой модели для данных, выбранных по последней цифре шифра, по табл. 12.

Таблица 12. Балансовая модель. Индивидуальные задания

№ варианта	Объем производства	Потребление отраслей	Спрос

Отчет по работе

Распечатки таблицы вычислений.

Литература: [2], c. 509-515.

Работа 4. ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ

Цель работы

Ознакомление с финансовыми функциями.