Сочетания спроса и стратегии производства

Тема 1. Принятие решений в условиях риска

И неопределенности

Цель задания: Изучить основные методические подходы к обоснованию принятия решений по заданным целям и ограничениям в ситуациях риска и неопределенности развития экономических процессов.

Принятие решений в условиях риска

Ситуация риска характеризуется тем, что в результате каждого действия могут быть получены различные результаты, вероятность которых известна или может быть определена на основе статистических данных, на основе экспертных оценок. В этом случае решение обычно принимается по критерию максимума ожидаемого среднего выигрыша, или минимума ожидаемого среднего риска.

Постановка задачи по оптимизации решений в ситуации риска

Возможны «m» решений (стратегий) Р₁ . . . Р_m ; условия обстановки (состояния природы) точно неизвестны, но о них можно сделать «n» предположений О₁. . . О_n; известны результаты – выигрыши а_ij (прибыль, доход, рентабельность или др), соответствующие каждому варианту сочетаний решений Р_i и обстановки О_j. Выигрыши являются показателями эффективности решений при различных вариантах обстановки. Эти данные оформляются таблицей эффективности (табл. 1).

Таблица 1 - Таблица эффективности

Варианты решений (Рi)	Выигрыши в зависимости от вариантов обстановки (ОJ)
О1	О2	и т.д.	Оn
Р1	а11	а12	. . .	а1n
и т.д.	. . .	. . .	. . .	. . .
Рm	аm1	аm2	. . .	аmn

Наличие выигрышей позволяет определить потери (ущерб, упущенные возможности) в результате принятия нерационального решения – в случае, когда ожидаемое условие обстановки, имеющее вероятностный характер, не произошло. Величину потерь (Н_ij) можно определить как разность между максимальным выигрышем при данных условиях обстановки (b_j) и выигрышами по каждому решению для данного варианта обстановки:

Н_ij = b_j – а_ij, (1)

где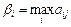

По этим данным строят таблицу рисков (таблицу потерь), аналогичную таблице эффективности.

Лучшей стратегией будет та, которая обеспечивает максимальный средний выигрыш (А_i) или минимальный средний риск (R_i), т.е. минимальные средние потери:

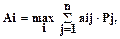(2)

где p_j – вероятности различных вариантов обстановки; а_ij – ожидаемые выигрыши для каждой пары сочетаний решений и вариантов обстановки;

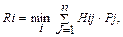(3)

где Н_ij – значение потерь, соответствующее различным вариантам обстановки.

Задача 1.На предприятии планируют начать производство новых видов продукции. При этом возможны 4 решения – Р₁, Р₂ , Р₃ и Р₄, каждому из которых соответствует определенный вид продукции или их комбинация. Варианты обстановки характеризует структура спроса на новую продукцию, при этом возможны 3 варианта состояния спроса – О₁, О₂ и О₃. Выигрыши, характеризующие величину результата ( дохода, прибыли), соответствующего каждой паре сочетаний решений «Р» и обстановки «О», представлены в таблице 2. Вероятность реализации вариантов обстановки (p_j) составляет: для варианта О₁ – 0,5, для О₂ – 0,3 и для О₃ – 0,2.

Необходимо выбрать наиболее выгодную стратегию производства.

Таблица 2 - Эффективность производства новых видов продукции

Варианты решений –стратегии производства (Рi)	Величина выигрыша (аij) в зависимости от состояния спроса
О1	О2	О3
Р1
Р2
Р3
Р4
bj = max aij

Методические указания к задаче 1

Для выбора более эффективного решения применяют показатель потерь, который определяет, насколько выгодна применяемая стратегия в данной конкретной обстановке с учетом степени её неопределенности.

1. Определить потери (Hij) для каждой пары сочетаний решений и обстановки как разность между максимальным выигрышем для конкретного варианта обстановки (см. последнюю строку таблицы 1) и выигрышем по каждому решению для данного варианта обстановки (формула 1). Величину потерь рассчитать в таблице 3.

Таблица 3 - Величина потерь прибыли при различных вариантах

сочетания спроса и стратегии производства

Варианты решений – стратегий производства (Рi)	Величина потерь (Нij) в зависимости от вариантов условий обстановки (Оj)
О1	О2	О3
Р1
Р2
Р3
Р4

2. Определить показатели риска (Ri) для каждого из решений (формула 3), по минимальному показателю выбрать наименее рискованное решение.