Определение основных статистических характеристик

Выборочный метод

Цель работы:

• ознакомление и освоение статистических функций Microsoft Excel;

• применение выборочного метода при обработке результатов анализа.

Теоретические сведения.

По охвату статистической совокупности исследование может быть сплошное или не сплошное. При сплошном статистическом исследовании группа наблюдения формируется путем полного охвата всех единиц изучаемого явления. Множество всех единиц наблюдения, охватываемых таким сплошным наблюдением, называется генеральной совокупностью.

Основным методом не сплошного наблюдения является выборочный метод. Если интересующая нас совокупность слишком многочисленна, либо ее элементы малодоступны, а так же если имеются другие причины (организационные, финансовые, физические и т. п.), не позволяющие изучать сразу все ее элементы, прибегают к изучению какой-то части этой совокупности. Эта выбранная для полного исследования группа элементов называется выборкой или выборочной совокупностью. Выборка — это группа элементов, выбранная для исследования из всей совокупности элементов. Задача выборочного метода состоит в том, чтобы сделать правильные выводы относительно всего собрания объектов, их совокупности.

Выборочная функция распределения.

Для построения выборочной функции распределения весь диапазон изменения случайной величины X разбивают на ряд интервалов одинаковой ширины. Число интервалов обычно выбирают не менее 5 и не более 15. Затем определяют число значений случайной величины X, попавших в каждый интервал. Поделив эти числа на общее количество наблюдений n, находят относительную частоту попадания случайной величины X в заданные интервалы. По найденным относительным частотам строят гистограммы выборочных функций распределения. Если соответствующие точки относительных частот соединить ломаной линией, то полученная диаграмма будет называться полигоном частот. Кумулятивная кривая будет получена, если по оси абсцисс откладывать интервалы, а по оси ординат — число или доли элементов совокупности, имеющих значение, меньшее или равное заданному. При увеличении до бесконечности размера выборки выборочные функции распределения превращаются в теоретические: гистограмма превращается в график плотности распределения, а кумулятивная кривая — в график функции распределения.

В Ехсеl для построения выборочных функций распределения используются специальная функция ЧАСТОТА и процедура пакета анализа Гистограмма. -Функция ЧАСТОТА вычисляет частоты появления случайной величины в интервалах значений и выводит их как массив цифр. Функция задается в качестве формулы массива.

ЧАСТОТА (массив данных; массив карманов). Здесь: • массив данных - это массив или ссылка на множество данных, для которых вычисляются частоты.

• массив карманов — это массив или ссылка на множество интервалов, в которые группируются значения аргумента массив данных.

Отметим, что количество элементов в возвращаемом массиве на единицу больше числа элементов в массив карманов. Дополнительный элемент в возвращаемом массиве содержит количество значений, больших, чем максимальное значение в интервалах.

Процедура Гистограмма используется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. Процедура выводит результаты в виде таблицы и гистограммы.

• во Входной диапазон вводится диапазон исследуемых данных;

• в поле Интервал карманов (необязательный параметр) может вводиться диапазон ячеек или необязательный набор граничных значений, определяющих выбранные интервалы (карманы). Эти значения должны быть введены в возрастающем порядке, В М5 Ехсе1 вычисляется число попаданий данных между началом интервала и соседним большим по порядку. При этом включаются значения на нижней границе интервала и не включаются значения на верхней границе. Если диапазон карманов не был введен, то набор интервалов, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически;

• рабочее поле Выходной диапазон предназначено для ввода ссылки на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически;

• переключатель Интегральный процент позволяет установить режим генерации интегральных процентных отношений и включения в гистограмму графика интегральных процентов;

• переключатель Вывод графика позволяет установить режим автоматического создания встроенной диаграммы на листе, содержащем выходной диапазон.

Практические задания

Пример Построить эмпирическое распределение веса студентов в килограммах для следующей выборки: 64, 57, 63, 62, 58, 61, 63, 60, 60, 61, 65, 62, 62, 60, 64, 61, 59,59, 63, 61, 62, 58, 58, 63,61, 59,62, 60, 60,58, 61, 60, 63, 63, 58, 60, 59, 60, 59, 61, 62, 62, 63, 57, 61, 58, 60, 64, 60, 59, 61, 64, 62, 59, 65.

Решение

1. В ячейку А1 введите слово Наблюдения, а в диапазон А2:Е12 — значения веса студентов.

2. Выберите ширину интервала 1 кг. Тогда при крайних значениях веса 57 кг и 65 кг получится 9 интервалов. В ячейки G1 и G2 введите названия интервалов Вес и кг, соответственно. В диапазон G4:G12 введите граничные значения интервалов (57, 58, 59, 60, 61, 62, 63, 64, 65).

3. Введите заголовки создаваемой таблицы: в ячейки Н1:Н2 — Абсолютные частоты, в ячейки I1:I2 — Относительные частоты, в ячейки J1:J2 — Накопленные частоты.

4. Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек Н4:Н12 (используемая функция ЧАСТОТА задается в виде формулы массива). В рабочее поле Массив данных введите диапазон данных наблюдений (А2:Е12). В рабочее поле Двоичный массив мышью введите диапазон интервалов (G4:G12). Последовательно нажмите комбинацию клавиш СTRL+SHIFT:+ЕNTER. В столбце Н4:Н12 появится массив абсолютных частот.

5. В ячейке Н13 найдите общее количество наблюдений. Убедитесь, что диапазон суммирования указан правильно (Н4:Н12),

6. Заполните столбец относительных частот. В ячейку J4 введите формулу для вычисления относительной частот: =Н4/$Н$13. Получим массив относительных частот.

7. Заполните столбец накопленных частот. В ячейку J4скопируйте значение относительной частоты из ячейки I4 (0,036364). В ячейку J5 введите формулу:=J4+I5. Нажмите клавишу ENTER. Cкопируйте введенную формулу в диапазон Jб:J12. Получим массив накопленных частот.

8. В результате после форматирования получим таблицу

Наблюдения						вес, кг.	абс. частоты	отн. част.	накопл. част
								0,03636	0,036363636
								0,10909	0,145454545
								0,12727	0,272727273
								0,18182	0,454545455
								0,16364	0,618181818
								0,14545	0,763636364
								0,12727	0,890909091
								0,07273	0,963636364
								0,03636

9. Постройте диаграмму относительных и накопленных частот.

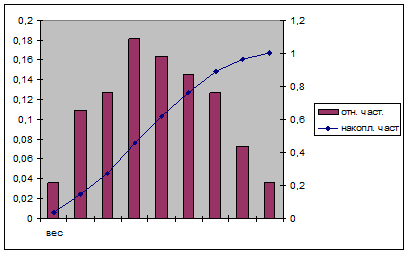
Рис. Диаграмма относительных и накопленных частот из примера 1

Упражнения:

1. Постройте эмпирические функции распределения (относительные и накопленные частоты) для результатов своего эксперимента по теме диссертационного исследования

2. Найдите распределение по абсолютным частотам для следующих результатов тестирования в баллах: 79, 85, 78, 85, 83, 81, 95, 88 и 97 (используйте границы интервалов 70,79,89).

3. Постройте эмпирические функции распределения (абсолютные и накопленныечастоты) успеваемости в группе из 20 студентов: 4, 4, 5, 3, 4, 5,4, 5, 3, 5, 3, 3, 5.4,1 5, 4, 3, 5, 3, 5.

Выборочные характеристики

Теоретические сведения.

Замена теоретической функции распределения F(х) на ее выборочный аналог F_n(х) в определении математического ожидания, дисперсии, стандартного отклонений и т.п. приводят к выборочному среднему, выборочной дисперсии, выборочному стандартному отклонению и т. д. Выборочные характеристики являются оценками соответствующих характеристик генеральной совокупности. Эти оценки должныудовлетворять определенным требованиям. В соответствии с важнейшими требованиями, оценки должны быть:

- несмещенными, то есть стремиться к истинному значению характеристики генеральной совокупности при неограниченном увеличении количества испытаний;

- состоятельными, то есть с ростом размера выборки оценка должна стремиться к значению соответствующего параметра генеральной совокупности с вероятностью, приближающейся к 1;

- эффективными, то есть для выборок равного объема используемая оценка должна иметь минимальную дисперсию.

Простейшим показателем, характеризующим центр выборки, является мода.

Мода— это элемент выборки с наиболее часто встречающимся значением (наиболее вероятная величина).

Среднее значение — это центр выборки, вокруг которого группируются элементы выборки. При увеличении числа наблюдений среднее приближается к математическому ожиданию. Среднее значение обозначается также буквой М.

Выборочная медиана — это число, которое является серединой выборки, то есть половина чисел имеет значения большие, чем медиана, а половина чисел имеет значения меньшие, чем медиана. Для нахождения медианы обычно выборку ранжируют — располагают элементы в порядке возрастания. Если количество членов ранжированного ряда нечетное, медианой является значение ряда, которое расположено посередине, то есть элемент с номером (п + 1)/2. Если число членов ряда четное, то медиана равна среднему членов ряда с номерами n/2 и n/2+1.

Основными показатели рассеяния вариант являются интервал, дисперсия выборки, стандартное отклонение и стандартная ошибка.

Интервал(амплитуда, вариационный размах) — это разница между максимальным и минимальным значениями элементов выборки. Интервал является простейшей и наименее надежной мерой вариации или рассеяния элементов в выборке.

Более точно отражают рассеяние показатели, учитывающие не только крайние, но ивсе значения элементов выборки.

Дисперсией выборки,или выборочным аналогом дисперсии, называется величина

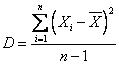
Дисперсия выборки — это параметр, характеризующий степень разброса элементов выборки относительно среднего значения. Чем больше дисперсия, тем дальше отклоняются значения элементов выборки от среднего значения.

Выборочным стандартным отклонением(среднее квадратичное отклонение) называется величина

s=√D

Это параметр, также характеризующий степень разброса элементов выборки относительно среднего значения. Чем больше среднее квадратичное отклонение, тем дальше отклоняются значения элементов выборки от среднего значения. Параметр аналогичен дисперсии и используется в тех случаях, когда необходимо, чтобы показатель разброса случайной величины выражался в тех же единицах, что и сред нее значение этой случайной величины. Часто выборочное стандартное отклоне­ние обозначают буквой а(сигма).

Стандартная ошибкаили ошибка среднегонаходится из выражения

M=S/√n

Стандартная ошибка — это параметр, характеризующий степень возможного отклонения среднего значения, полученного на исследуемой ограниченной выборке, от истинного среднего значения, полученного на всей совокупности элементов. С помощью стандартной ошибки задается так называемый доверительный интервал. 95%-ный доверительный интервал, равный х ұ 2т, обозначает диапазон, в который с вероятностью p = 0,95 (при достаточно большом числе наблюдений п > 30) попадает среднее генеральной совокупности МХ.

Выборочной квантильюназывается решение уравненияF_n(х) = р.

В частности, выборочная медиана есть решение уравненияF_n(х) =0,5.

Показателями, характеризующими форму распределения, являются выборочные эксцесс и асимметрия.

Эксцесс— это степень выраженности «хвостов» распределения, то есть частоты появления удаленных от среднего значений.

Асимметрия— величина, характеризующая несимметричность распределения элементов выборки относительно среднего значения. Принимает значения от -1 до 1. В случае симметричного распределения асимметрия равна 0.

Часто значения асимметрии и эксцесса используют для проверки гипотезы о том. что данные (выборка) принадлежат к определенному теоретическому распределению, в частности, нормальному распределению. Для нормального распределения асимметрия равна нулю, а эксцесс — трем.

Определение основных статистических характеристик

Цель работы:

• познакомиться со статистическими функциями Microsoft Excel;

• использование специальных функций при обработке результатов анализа

Теоретические сведения.

В результате наблюдений или эксперимента получаются наборы данных, называемые выборками. Для проведения их анализа данные подвергаются статистической обработке. Первое, что всегда делается при обработке данных, это вычисление элементарных статистических характеристик выборок (как минимум: среднего, среднеквадратичного отклонения, ошибки среднего) по каждому параметру и по каждой группе. Полезно также вычислить эти характеристики для объединения родственных групп и суммарно по всем данным.