Стоимость денег во времени

Концепция стоимости денег во времени состоит в том, что денежные средства имеют стоимость, которая определяется временным фактором, т. е. ресурсы, имеющиеся в распоряжении сегодня, стоят больше, чем те же ресурсы, получаемые через некоторый (существенный) промежуток времени.

Концепция стоимости денежных средств затрагивает широкий круг деловых решений, связанных с инвестированием. Понимание данной концепции во многом определяет эффективность принимаемых решений.

Временное предпочтение в распоряжении денежными средствами определяется следующим. Текущее распоряжение ресурсами позволяет предпринимать действия, которые с течением времени приведут к росту будущего дохода. Исходя из этого, стоимость денежных средств характеризуется возможностью получить дополнительный доход. Чем больше возможная величина дохода, тем выше стоимость денежных средств. Таким образом, стоимость денежных средств определяется упущенной возможностью получить доход в случае наилучшего варианта их размещения.

Данное положение имеет большое значение, поскольку стоимость денежных средств часто ошибочно сводят к потерям от инфляции. Действительно, под влиянием инфляционного фактора покупательная способность денежных средств снижается. Но принципиальным становится понимание того, что даже при полном отсутствии инфляции денежные средства обладают стоимостью, определяемой отмеченным ранее временным предпочтением и возможностью получения дополнительного дохода от более раннего вложения средств.

Количественным выражением временного предпочтения в использовании денежных средств обычно выступают процентные ставки, отражающие норму временного предпочтения в данной экономической ситуации.

Но если ставка процента отражает большую ценность ресурсов, имеющихся в распоряжении сейчас, то из этого следует, что для определения приведенной к сегодняшнему моменту стоимости денежных средств, которые предполагается получить в будущем, необходимо дисконтировать эти суммы в соответствии со ставкой процента.

Инвестирование представляет собой обычно длительный процесс, в оценке инвестиций часто приходится сравнивать стоимость денег в начале их инвестирования со стоимостью денег при их возврате в виде будущей прибыли, амортизационных отчислений и т.п.

Точкой приведения может быть:

— начало инвестиционного проекта — «0» (начало первого шага);

— первый год — «0—1» (первый шаг);

— год завершения инвестиций (строительства) — «3»;

— последний год жизненного цикла инвестиций (расчетного периода) — «7—8»;

— окончание жизненного цикла (расчетного периода) — «8» и др.

Приведение по шкале времени может осуществляться на основе процессов наращения и дисконтирования. Наращение — это процесс определения возвращаемой (будущей) суммы денежных средств, если известны исходная сумма вложений, процентная ставка дохода от них и период накопления.

FV=PV*(1+E)ⁿ

Дисконтирование — процесс приведения денежных сумм, получаемых в будущем, к более раннему (начальному) моменту времени.

PV=FV*(1/(1+E)ⁿ)

Таким образом, в процессе сравнения стоимости денежных средств при их инвестировании и возврате принято использовать два основных понятия:

— будущая стоимость денег, FV;

— настоящая (текущая, современная) стоимость денег, PV.

Будущая стоимость денег представляет собой сумму инвестированных в настоящий момент средств PV, в которую они превратятся через некоторый период времени Тс учетом определенной ставки процента Е. Определение будущей стоимости связано с процессом наращения этой стоимости, которое представляет собой поэтапное увеличение суммы вклада путем присоединения к его первоначальному размеру суммы процентов.

Будущая стоимость, или сложный процент, рассчитывается по так называемой процентной ставке. В инвестиционных расчетах процентная ставка применяется не только как инструмент наращения стоимости денежных средств, но и в более широком смысле — как измеритель степени доходности инвестиционных операций.

Настоящая (текущая, современная) стоимость денег представляет собой сумму будущих денежных поступлений, приведенных с учетом определенной ставки процента (так называемой дисконтной ставки) к настоящему периоду.

Сложный процент

Сложные проценты - сложное начисление, при котором проценты начисляются несколько раз за период и не выплачиваются, а накапливаются на сумму основного долга. Этот механизм особенно эффективен при среднесрочных и долгосрочных кредитах.

При начислении сложных процентов (после n лет (периодов) наращения) наращенная сумма определяется по формуле

S = P (1 + i ) ⁿ ,

где i – ставка сложных процентов, выраженная в коэффициенте; n – число начислений сложных процентов за весь период.

Доля расчетов с использованием сложных процентов в финансовой практике достаточно велика. Расчеты по правилу сложных процентов часто называют начисление процентов на проценты, а процедуру присоединения начисленных процентов – их реинвестированием или капитализацией.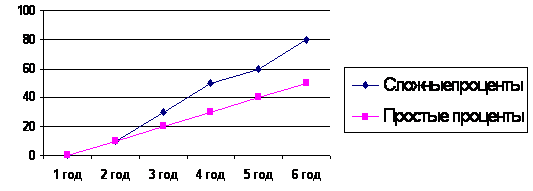

Рис. 1. Динамика увеличения денежных средств при начислении простых и сложных процентов

Из-за постоянного роста базы вследствие реинвестирования процентов рост первоначальной суммы денег осуществляется с ускорением, что наглядно представлено на Рис. 1.

В финансовой практике обычно проценты начисляются несколько раз в году. Если проценты начисляются и присоединяются чаще (m раз в год), то имеет место m-кратное начисление процентов. В такой ситуации в условиях финансовой сделки не оговаривают ставку за период, поэтому в финансовых договорах фиксируется годовая ставка процентов i, на основе которой исчисляют процентную ставку за период ( 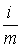). При этом годовую ставку называют номинальной, она служит основой для определения той ставки, по которой начисляются проценты в каждом периоде, а фактически применяемую в этом случае ставку (( 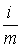)^mn) – эффективной, которая характеризует полный эффект (доход) операции с учетом внутригодовой капитализации.

Наращенная сумма по схеме эффективных сложных процентов определяется по формуле

S = P (1+ 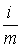)^mn ,

где i – годовая номинальная ставка, %; (1+ 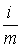)^mn – коэффициент наращения эффективной ставки; m – число случаев начисления процентов за год; mn – число случаев начисления процентов за период.

Следует отметить, что при периоде, равным 1 году, число случаев начисления процентов за год будет соответствовать числу случаев начисления процентов за весь период. Если, период составляет более 1 года, тогда n будет соответствовать этому значению.

Начисление сложных процентов также применяется не только в случаях исчисления возросшей на проценты суммы задолженности, но и при неоднократном учете ценных бумаг, определении арендной платы при лизинговом обслуживании, определении изменения стоимости денег под влиянием инфляции и т. д.

Как говорилось выше, ставку, которая измеряет относительный доход, полученный в целом за период, называют эффективной. Вычисление эффективной процентной ставки применяется для определения реальной доходности финансовых операций. Эта доходность определяется соответствующей эффективной процентной ставкой.

Эффективную процентную ставку можно рассчитать по формуле

I_эф = (1+ 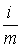)^mn – 1 .

Расчет эффективной процентной ставки в финансовой практике позволяет субъектам финансовых отношений ориентироваться в предложениях различных банков и выбрать наиболее приемлемый вариант вложения средств.