Раздел 4. СТАНДАРТНЫЕ ФУНКЦИИ

Под функцией понимается зависимость одной переменной (y) от одной (х) или нескольких переменных (х₁, х₂,...х_n), причем каждому набору значений переменных х₁, х₂,...х_n будет соответствовать единственное значение зависимой переменной у определенного типа.

Функции вводят в состав формул, либо отдельно. В электронных таблицах могут быть представлены следующие виды функций:

· математические;

· статистические;

· текстовые;

· логические;

· финансовые;

· функции даты и времени и др.

Математические функции выполняют различные математические операции, например, вычисление логарифмов, тригонометрических функций, преобразование радиан в градусы и т.п.

Статистические функции выполняют операции по вычислению параметров случайных величин или их распределений, представленных множеством чисел, например, стандартного отклонения, среднего значения и т.п.

Текстовые функции выполняют операции над текстовыми строками или последовательностью символов, вычисляя длину строки, преобразовывая заглавные буквы в строчные и т.п.

Логические функции используются для построения логических выражений, результат которых зависит от истинности проверяемого условия.

Финансовые функции используются в сложных финансовых расчетах, например, определения нормы дисконта, размера ежемесячных выплат для погашения кредита, амортизационных отчислений и др.

Все функции имеют одинаковый формат записи и включают имя функции и находящийся в круглых скобках перечень аргументов, разделенных запятыми.

Мастер функций

Если в формуле используются функции, щелкните по кнопке Мастер функций , расположенной на панели формул,при этом раскроется окно диалога Мастера функций. Ввод функции состоит из двух шагов.

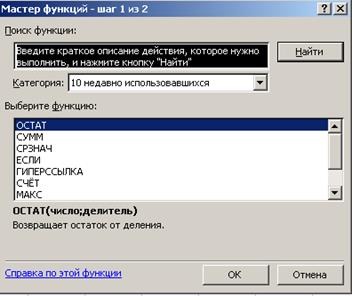На первом шаге раскрывается карточка выбора необходимой функции: в окне Категория выбирается вид функции, а затем в окнеВыберите функцию выбирается необходимая функция, при этом выбранная функция будет помещена в строку формул. Если с данной функцией Вы работаете в первый раз, то полезно прочитать справку, нажав кнопку Справка. Затем перейти ко второму шагу работы с Мастером функций, нажав кнопкуДалее.

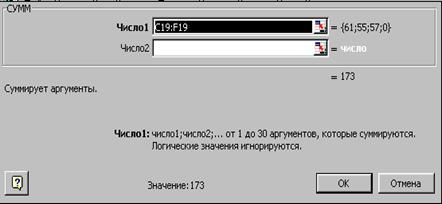На втором шаге в соответствующие поля вводятся поочередно аргументы функции, количество которых зависит от вида функции. Аргументами функции могут быть адреса ячеек, адрес блока клеток и в редких случаях константы. Аргумент может так же представлять сложное выражение и включать все компоненты формул. Если аргумент включает стандартные функции, то они берутся из Мастера функций, его кнопка находится слева от поля ввода аргумента. Для окончания ввода аргумента щелкните левой кнопкой мыши в поле ввода следующего аргумента. По мере ввода аргумента его значение вычисляется и показывается справа от поля ввода. Задав все аргументы функции нужно нажать кнопку Готово, приэтом в ячейке появиться результат вычисления по заданной функции, сама функция отобразится в строке формул. До нажатия кнопкиГотово любой параметр можно исправить и даже вернуться на шаг назад для выбора другой функции.

Некоторые функции вообще не имеют аргументов (например, функцияp - ПИ), в этом случае на первом шаге можно сразу нажать кнопку Готово.

Вложенные функции

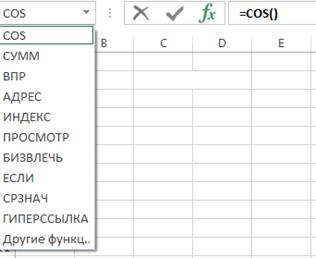
Часто бывает необходимо вводить сложную функции, когда внутри одной функции нужно вызывать другую. Например, 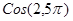.Аргументом функции COS является функция ПИ. Для вызова какой-либо стандартной функции внутри текущей, нужно раскрыть список (в примере список раскрывается около функции COS) и выбрать нужную функцию (в примере ПИ). Если нужной функции в списке не окажется, нужно выбрать Другие функции. Откроется окно Мастера функций, и в нем нужно будет ввести искомую функцию (в примере ПИ).

ЛАБОРАТОРНАЯ РАБОТА № 5
«Математические и статистические функции»

Цель работы – написание формул с использованием мастера функций, изучение статистических и математических функций.

В таблице показаны некоторые математические и статистические функции, наиболее часто используемые в Excel.

Функции и аргументы	Возвращаемое значение
СРЗНАЧ (список аргументов)	Среднее арифметическое из значений всех аргументов
МАКС (список аргументов)	Максимальное число из списка аргументов
МИН(список аргументов)	Минимальное число из списка аргументов
ПРОИЗВЕД (список аргументов)	Произведение значений аргументов
ОСТАТ(число;делитель)	Возвращает остаток от деления аргумента число на делитель. Результат имеет такой же знак, как и делитель.
СЧЁТ(значение1; значение2; ...)	Подсчитывает количество чисел в списке аргументов. Функция СЧЁТ используется для получения количества числовых ячеек в интервалах или массивах ячеек.
КОРЕНЬ (число)	Корень квадратный из числа
ФАКТР (число)	Факториал целого числа, заданного в качестве аргумента
СЛЧИС ()	Случайное число в интервале от 0 до 1
ABS(число)	Модуль значений аргумента
LN(число)	Натуральный логарифм числа (по основанию е=2,71828...)
EXP(число)	Экспонента числа (ех)
SIN(число)	Синус числа, заданного в радианах
COS(число)	Косинус числа, заданного в радианах
TAN(число)	Тангенс числа, заданного в радианах

ЗАДАНИЕ 1

1. Перейти на новый лист и назвать его «Статистика».

2. На лист «Статистика» скопировать с листа «Прибыль» таблицу прибыли предприятий (таблица 3).

3. Используя таблицу 3 (Прибыль предприятий) из лабораторной работы 3 нужно рассчитать для каждой из фирм:

1. максимальную,

2. минимальную,

3. среднюю прибыль, используя статистические функции МАКС, МИН, СРЗНАЧ.

4. Оформить расчеты в виде таблицы «Результаты вычислений».

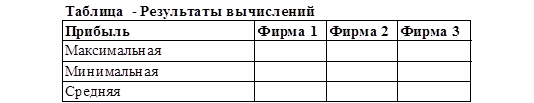
ЗАДАНИЕ 2

1. Перейти на новый лист и назвать его «Тригонометрические функции».

2. Используя стандартные математические функции SIN, COS, TAN рассчитать значения функций Sin(x), Cos(x), Tg(x) при изменении аргумента функции от –1 до +1 с шагом 0,1. Для записи значений аргумента x написать формулу: предыдущее значение плюс 0,1. Расчет оформить в виде таблицы «Тригонометрические функции». Формат для аргумента х – числовой с двумя десятичными знаками. Формат для значений функции – числовой, с четырьмя десятичными знаками.

Тригонометрические функции

X	Cos(x)	Sin(x)	Tg(x)

3. На этом же листе построить графики функций в одной системе координат. График должен иметь название, название осей, легенду. В качестве вида графика лучше выбрать – диаграмма точечная.

ЗАДАНИЕ 3

1. Перейдите (создайте) на новый лист книги и назовите его «Функция вложенная».

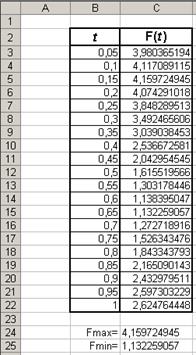
2. Получите результаты вычисления формулы 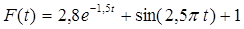на множестве значений аргумента tÎ{0,05; 0,1; 0,15; 0,2;…, 0,95; 1}. Для записи значений аргумента t написать формулу: предыдущее значение плюс 0,05. При записи формулы в Excel вместо t нужно делать ссылку на ячейку, в которой хранится значение аргумента t (в примере это ячейка В3).

3. С помощью стандартных функций найдите максимальное и минимальное значение функции F(t).

4. Оформите результаты вычисления формулы в следующем виде:

5. Постройте график функции F(t).

ЛАБОРАТОРНАЯ РАБОТА № 6
«Использование абсолютных и относительных ссылок»

Адресация ячеек

Абсолютная ссылка – это не изменяющийся при копировании и перемещении формулы адрес ячейки, содержащей исходное данное (операнд).

Для указания абсолютной адресации вводится символ $. Различают два типа абсолютной ссылки: полная и частичная.

Полная абсолютная ссылка указывается, если при копировании или перемещении адрес ячейки, содержащей исходное данное, не меняется. Для этого символ $ ставится перед наименованием столбца и номером строки.

$В$5; $D$12 – полные абсолютные ссылки.

Частичная абсолютная ссылка указывается, если при копировании и перемещении не меняется номер строки или наименование столбца. При этом символ $ в первом случае ставится перед номером строки, а во втором – перед наименованием столбца.

В$5; D$12 – частичная абсолютная ссылка, не меняется номер строки;

$В5; $D12 – частичная абсолютная ссылка, не меняется наименование столбца.

Относительная ссылка– это изменяющийся при копировании и перемещении формулы адрес ячейки, содержащей исходное данное (операнд). Изменение адреса происходит по правилу относительной ориентации ячейки с исходной формулой и ячеек с операндами.

Форма написания относительной ссылки совпадает с обычной записью адреса ячейки.

Правила адресации ячеек:

1. В формуле пишутся относительные ссылки на ячейки той же таблицы, в которой создается формула, и абсолютные ссылки на ячейки, расположенные вне этой таблицы.

2. Для записи абсолютного адреса ячейки достаточно написать её относительный адрес и нажать функциональную клавишу F4.