Kiölçülü massivlər

İkiölçülü massivlər ( matrislər) – vektorlar massividir və kvad­rat mötərizədə iki ədədlə verilirlər.

Elementin_ tipi massivin_adı [ölçü 1] [ölçü 2];

Burada ölçü 1 – sətirlərin sayı, ölçü 2 – sütunların sayı­dır.

Üçölçülü massivlər:

Elementin_tipi massivin_adı [ölçü 1] [ ölçü 2][ölçü 3];

Məsələn:

double matre [100][10];

int i_matrix [10] [20];

char cube [10][20][3];

Kompüterin yaddaşında matrislər aşağıdakı ardıcıllıqla yer­ləş­dirilmiş oyuqları tuturlar: əvvəlcə I sətir, sonra II sətir və s.

Çoxölçülü massivlərin emalında bir-birinə daxil olan dövr­­­lərdən istifadə edilir. Bu vaxt ən yavaş sol kənar indeks, ən tez isə sağ kənar indeks dəyişir.

Çoxölçülü massivlərlə işləyərkən ən daxili dövr sağ kə­nar­, ən xarici dövr isə sol kənar indeksə uyğun gəlir.

Ikiölçülü massivlərin də emalı zamanı bir sıra tipik al­qo­ritm­­lər istifadə olunur. Onlardan bir neçəsini verək.

Klaviaturadan tamqiymətli matrisin daxil edil­məsi:

const int max_row=5;

const int max_col=4;

. . . . . . . . . . .

for (i=0; i<max_row; i++)

{ for ( j=0; j< max_ col; j++)

{ printf (“ \ n x [%d][%d]”, i, j);

scanf (“%d, &x[i][j]); }

}

İkiölçülü massivin ekrana çıxarılması:

const int max_row=5;

const int max_col=4;

. . . . . . . . . . .

for (i=0; i<max_row; i++)

{ for ( j=0; j< max_ col; j++)

printf (“ %4d”, x [i] [j]” );

printf (“ \ n” ); }

}

Massivin maksimal elementinin hesablanması:

. . . . . . . . . .

int arr [n][k], max;

. . . . . . . . . . .

max=arr [0][0];

for (i=0; i<n; i++)

for (j=0; j<k; j++)

{ if (max< arr [i][j]) max=arr [i][j]; }

Matrisin hər sətrinin maksimal elementinin tapılması:

int arr [n][k], int max[n];

. . . . . . . . . . .

for (i=0; i<n; i++)

{ max[i]=arr [i][0];

for (j=0; j<k; j++)

if (max[i]< arr [i][j]) max[i]=arr [i][j]; }

}

Misal 7.3. Matrisdə sıfırdan kiçik qiymətli ilk elementin yerini təyin edən proqram yazın.

#include <stdlib.h>

main()

{

int a[10][10];

int i, j;

randomize();

for (i = 0; i<10; i++)

for (j = 0; j<10; j++)

a[i][j] = (rand() % 100) - 20;

for (i = 0; i<10; i++)

for (j = 0; j<10; j++)

if (a[i][j] < 0)

goto bul;

printf("Sıfırdan kiçik element yoxdur\n");

goto son;

bul:

printf("elementin mövqeyi və qiyməti (%d, %d) = %d \n",i, j, a[i][j]);

son:

return 0;

}

Misal 7.4. “Qabarcıq” üsulu ilə massivlərin nizam­lan­ması

#include<stdio.h>

#define n 1000

int main() {

int n, i, j;

int a[n];

scanf("%d", &n);

for(i = 0 ; i < n; i++) {

scanf("%d", &a[i]);

}

for(i = 0 ; i < n ; i++) {

//iki qonşu elementin müqayisəsi

for(j = 0 ; j < n - i - 1 ; j++) {

if(a[j] > a[j+1]) {

// əgər şərt doğrudursa,onda

// onların yerləri dəyişdirilir.

int tmp = a[j]; a[j] = a[j+1] ; a[j+1] = tmp;

}

}

}

}

n elementli massivlərin nizamlanması üçün n-1 sayda əmə­liy­yat lazımdır.

Misal 7.5. Binomial əmsalların hesablanması (Paskal üç­­bucağı)

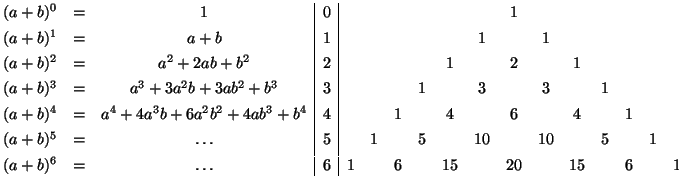
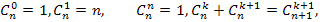
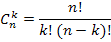
#include <stdio.h>

#define N 1000

long c[N];

int main () {

long n, i, j;

scanf ("%ld",&n);

for(i = 1; i <= n ; i++) c[i] =0;

c[0] = 1;

for(j = 1 ; j <= n; j++)

for(i = j; i >= 1 ; i--)

c[i] = c[i-1] + c[i];

for(i = 0; i <= n ; i++)

printf ("%ld ", c[i]);

return 0;

}