Решение контрольного примера с помощью Excel

1.4.1. Итак, после построения математической модели, необходимо перенести её в ЭТ Excel. Этот процесс, как для данного контрольного примера, так и для всех последующих решаемых задач оптимизации, может быть реализован в виде последовательности следующих этапов.

· Продумайте организацию исходных данных модели и введите их (коэффициенты целевой функции и ограничения) в ЭТ, снабдив понятными названиями.

· Зарезервируйте n отдельных ячеек для независимых переменных математической модели.

· В одной из ячеек создайте формулу, определяющую целевую функцию.

· Выберите ячейки и создайте в них формулы, соответствующие правым частям ограничений.

· Запустите программу Поиск решения для решения задачи.

· Проанализируйте полученное решение и отчеты, и определите возможные пути улучшения решения за счет снятия каких-либо ограничений.

· Вновь решите задачу с измененными исходными данными (возможно несколько раз, до получения наилучшего решения).

1.4.2. Детально рассмотрим последовательность действий по реализации этих этапов для решения задачи контрольного примера с помощью ЭТ Excel.

1.4.2.1. Любым известным вам способом загрузите программу Excel.

1.4.2.2. Для ввода исходных данных создайте таблицу, приведенную на рис. 1.4.1 (безусловно, это один из вариантов организации исходных данных, возможны и многие другие).

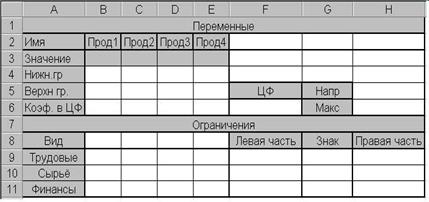
Рис. 1.4.1

Как видно на рис. 1.4.1, в таблицу введены названия элементов модели (затенённые ячейки), но они являются лишь оформлением решения задачи и на результат не влияют.

1.4.2.3. В созданную форму, введите исходные данные (Рис. 1.4.2).

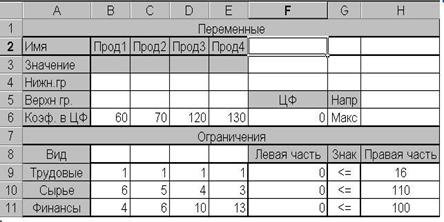
Рис. 1.4.2

Коэффициенты целевой функции, выражающие прибыль от производства единицы продукции каждого вида (единичная прибыль), записаны в ячейки B6:E6.

Коэффициенты ресурсных ограничений, определяющие потребность в каждом из видов ресурсов для производства единицы продукции, размещены в ячейках B9:E11. В ячейках Н9:Н11 записаны правые части ограничений на ресурсы, выражающие их имеющиеся в наличии объёмы.

1.4.2.4. Для независимых переменных задачи – искомых объёмов производства Прод1-Прод4 - зарезервированы ячейки В3:Е3. Решение задачи и должно определить оптимальные значения именно этих величин.

Переменные, определяющие

принимаемое решение:

П1 П2 П3 П4

¯ ¯ ¯ ¯

Ячейки электронной таблицы:

B3 C3 D3 E3

Следующий шаг связан с вводом целевой функции в ячейку F6. При этом алгебраическая формула, выражающая целевую функцию, должна быть трансформирована в так называемую клеточную формулу, которая содержат не имена переменных, а адреса ячеек, в которых находятся эти переменные.

Целевая функция в виде

алгебраического уравнения:

60*П1+70*П2+120*П3+130*П4

¯ ¯ ¯ ¯

Целевая функция в виде

Формулы ЭТ:

B6*B3+C6*C3+D6*D3+E6*E3

Клеточную формулу целевой функции можно вводить в виде выражения B6*B3+C6*C3+D6*D3+E6*E3, но удобне в виде функции СУММПРОИЗВ.

Введем целевую функцию в виде этой функции в ячейку F6:

- Установить курсор на ячейку F6 ;

- В Строке формул нажать кнопку Изменить формулу (=);

- После появления в поле ввода формул знака равенства, в поле Функции отображается функция, которая была использована последней. Если это функция СУММПРОИЗВ, щелкните по ней мышкой, если нет, щелкните стрелку справа от поля функций для просмотра списка из десяти последних функций, если и среди них нет СУММПРОИЗВ, выберите пункт Другие функции в нижней части списка, для вывода на экран диалогового окна Мастер функций. (Появившееся на экране диалоговое окно может закрыть саму таблицу, его можно перетащить ниже таблицы, «ухватившись» мышкой за заголовок окна);

- В окне Мастер функций – шаг 1 из 2 в окне Категория щелкните Математические, а в окне Функция на СУММПРОИЗВ и ОК;

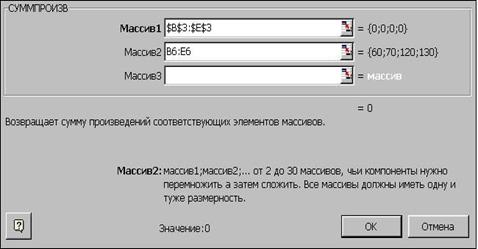
Рис. 1.4.3

- На экране появляется диалоговое окно СУММПРОИЗВ (Рис. 1.4.3), в поля которого Массив1, Массив2 вводятся адреса блоков ячеек, содержимое которых надо сначала попарно перемножить, а затем сложить. В поле Массив1 надо ввести адрес блока B3:E3.

Напомним, что ЭТ Excel автоматически изменяет относительные адреса ячеек (B3:E3) при копировании или переносе формул. Адрес блока независимых переменных надо будет копировать в другие ячейки без изменения, поэтому его необходимо записатьв абсолютной форме - B$3:E$3 (или $B$3:$E$3).

Этот и последующие адреса в формулах можно непосредственно вводить с клавиатуры, но удобнее и быстрее вводить адреса методом протаскивания мыши по ячейкам, чьи адреса следует ввести. Если адрес блока введен протаскиванием, необходимо, нажав клавиши F4, преобразовать его из относительной формы в абсолютную, добавив знаки $.

- В окно Массив2 введите B6:E6, после чего щелкните ОК

Формулы для наглядности можно вводить (но не обязательно) в режиме представления формул (включение/выключение этого режима - команда Сервис - Параметры – вкладка Вид – Формулы).

1.4.2.6. Следующий шаг связан с построением ограничений. Для каждого ограничения, содержащегося в алгебраической модели, необходимо создать клеточную формулу и поместить её в соответствующую ячейку.

Алгебраическая формула для ограничений:

- по первому ресурсу:

1 * П1 + 1 * П2 + 1 * П3 + 1 * П4

¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯

- формула для ячейки F8:

B9 * B3 + C9 * C3 + D9 * D3 + E9 * E3

- по второму ресурсу:

4 * П1 + 6 * П2 + 10 * П3 + 13 * П4

¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯

- формула для ячейки F9:

B10*B3 + C10*C3 + D10*D3 + E10*E3

- по третьему ресурсу:

6 * П1 + 5 * П2 + 4 * П3 + 3 * П4

¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯

- формула для ячейки F10:

B11*B3 + C11*C3 + D11* D3+ E11* E3

1.4.2.7. Вышеприведённые формулы ограничений отличаются от формулы целевой функции только одним сомножителем, поэтому формулу из ячейки F6 можно скопировать в буфер(ячейка после этого будет отмечена «бегущей» рамкой), а из буфера вставить в ячейку F9. При копировании она преобразуется в формулу для ограничения по первому ресурсу:

СУММПРОИЗВ(B$3:E$3;B9:E9)

1.4.2.8. Далее формулу из ячейки F9необходимо скопировать в ячейки F10 и F11 (либо также через буфер, либо, что быстрее, за маркер ячейки с нажатой левой клавишей мыши).В этих ячейках формулыпримут вид - СУММПРОИЗВ (B$3:E$3;B10:E10) и СУММПРОИЗВ (B$3:E$3;B11:E11).

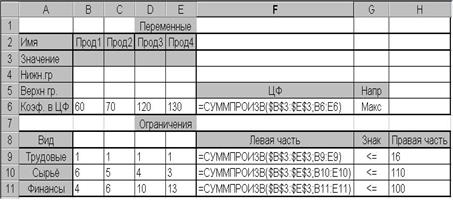
Рис. 1.4.4

После выполнения этих действий в режиме отображения формул ЭТ примет вид, показанный на рис. 1.4.4.

1.4.2.9. Введя исходные данные и зависимости для целевой функции можно приступить к поиску решения. Для решения оптимизационных задач в ЭТ Excel используется команда ПОИСК РЕШЕНИЙ меню СЕРВИС.

Эта команда оперирует с тремя основными компонентами построенной в ЭТ оптимизируемой модели:

· ячейкой, содержащей целевую функцию задачи;

· изменяемыми ячейками, содержащими независимые переменные;

· ячейками, содержащими левые части ограничений на имеющиеся ресурсы, а также простые ограничения на независимые переменные.

Рассмотрим последовательность ввода этих компонентов.

· Курсор в ячейку F6 икоманда Сервис – Поиск решения. На экране диалоговое окно Поиск решения (рис. 1.4.5).

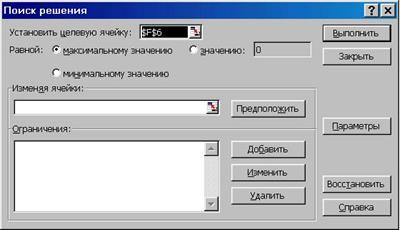
Рис. 1.4.5

· В окне Поиск решений пока заполнено только поле Установить целевую ячейку, в котором должен стоять адрес $F$6;

· Установить флажок на поиск максимального значения, если он не установлен (если бы решение должно было быть минимальным или равным заданной величине, устанавливаются соответствующие флажки и вводится значение заданной величины).

· В поле Изменяя ячейки ввести адреса искомых переменных –$B3:$E3, набором на клавиатуре или протаскиванием мыши.

1.4.2.8. Затем следует ввести ограничения - щелкнуть по кнопке Добавить – на экране появляется диалоговое окно Добавление ограничения (рис. 1.4.6).

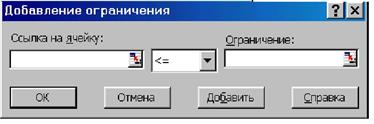
Рис. 1.4.6.

Первоначально вводятся граничные условия на значения переменных П1 - П4. При этом в левое поле вводится адрес ячейки (указанием мышью), содержимое которой должно удовлетворять заданному ограничению. В следующее поле вводится знак отношения для сравнения с ограничением – больше (>=), равно (=) или меньше (<=).Правое поле служит для задания значения ограничения в виде числовой константы или указания адреса ячейки, где такое значение содержится. Если ограничения по видам ресурсов имеют разные знаки отношений, то их придется вводить поочередно, например – В3 >= В4; B3 <= B5 и т.д. В нашем примере объёмы производства П1 – П4 - числа положительные, т.е. все больше или равны 0, поэтому нижние границы, т.е. ячейки В4:Е4 либо заполняются нулями, либо остаются пустыми, что равнозначно нулям. В этом случае ограничения можно ввести блоками В3:Е3>=В4:Е4. В завершение ввода ограничения – щелчок по кнопке Добавить (Рис. 1.4.7).

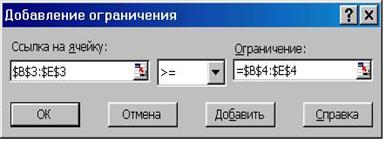
Рис. 1.4.7

Всего в нашем примере необходимо ввести 7 ограничений двумя блоками – четыре на объёмы производства по видам

продукции (уже введены), и три на ресурсы, которые и необходимо добавить. Как уже говорилось, величина потребного ресурса должна быть меньше или равна имеющемусяресурсу, т.е. можно записать, что блок F9:F11 <= Н9:Н11.

1.4.2.10. После ввода последнего ограничения и щелчка по кнопке Добавить, появляется очередное окно Добавление ограничения, которое нужно отменить, поскольку все ограничения уже введены. После закрытия окна Добавление ограничения в поле Ограничения окна Поиск решения появятся все введенные ограничения (Рис. 1.4.8).

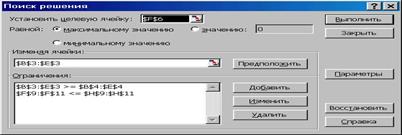
Рис. 1.4.8

1.4.2.11. Теперь, когда все ограничения для поиска оптимального решения заданы, воспользовавшись кнопками Изменить и Удалить можно ввести изменения либо удалить ряд ограничений из их списка. Для того, чтобы пользователь мог, изменяя параметры, несколько раз последовательно повторить поиск оптимального решения, записи в диалоговом окне Поиск решения сохраняются на протяжении всего сеанса работы с текущей рабочей книгой. Если необходимо сохранить эти параметры до следующего сеанса работы, следует сохранить рабочую книгу.

1.4.2.12. Дополнительные параметры, определяющие способ выполнения вычислений, можно задать нажатием на кнопку

Параметры в диалоговом окне Поиск решения (Рис. 1.4.8). В открывшемся диалоговом окне Параметры поиска решения (Рис. 1.4.9), необходимо установить флажки соответствующие линейным моделям.

1.4.2.13. Чтобы сохранить текущую модель и иметь возможность в дальнейшем работать с дополнительными моделями, следует нажать кнопку Сохранить модель.

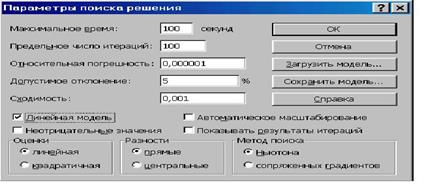
Рис. 1.4.9

1.4.2.14. Нажав кнопку ОК в окне Параметры поиска решения, на экран вновь вызывается окно Поиск решения (Рис. 1.4.8), на котором необходимо, нажав кнопку Выполнить, запустить процесс вычислений.

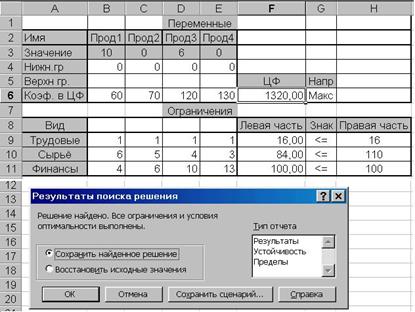
Рис. 1.4.10

Если вычисления оказались успешными, после завершения поиска решения новые значения будут вставлены в таблицу, и на экране появится диалоговое окно Результаты поиска решения, содержащее информацию о завершении процесса поиска решения (Рис. 1.4.10). На рисунке видно, что в оптимальном решении :

- объём выпуска продукции П1 составляет 10 единицы (В3=10);

- объём выпуска продукции П3 составляет 6 единицы (D3=6);

- объёмы выпуска продукции П2 и П4 составляет 0 единиц.

При этом максимальная прибыль будет составлять 1320 единиц (F6), а количество использованных ресурсов равно:

- трудовых – 16 единиц, т.е. использован весь ресурс без остатка;

- сырьё – 84 единицы, т.е. 26 единиц остатка;

- финансы – 100 единиц, т.е. использован весь ресурс.

Найденное решение можно сохранить или отказаться от него. Если выбрать опцию Восстановить исходные значения, то найденные значения будут удалены и появится возможность проконтролировать правильность введенных данных, и при необходимости исправить их.

Кнопка Сохранить сценарий служит для отображения на экране диалогового окна, в котором можно выполнить сохранение сценария решения задачи, чтобы использовать его в дальнейшем. Последовательность действий в этом случае будет рассмотрена в разделе анализа решения.