Математическая модель транспортной задачи

Для построения математической модели надо определить переменные решения, записать целевую функцию и сформировать ограничения. Обозначим через x(ij)количества (объемы) грузов, пере­возимых из пункта Оi, в пункт Нj (i принимает значения от 1 до n, а j — от 1 до m). Это переменные решения.

Переменные решения x₁₁, x₁₂…xn,m количества (объемы) грузов, перевозимых из пунктов отправления О₁, О₂,..., Оn в пункты назначения Н₁, Н₂,..., Нm соответственно. Всего имеем n*m переменных. На эти переменные налагаются условия неотрицательности.

Переменные принятия решений и удельные стоимости перевозок удобно записать в виде матриц переменных решений X:

x11	x12	…	x1m
x21	x22	…	x2m
…	…	…	…
xn1	xn2		xnm

и стоимостей С:

с11	c12	…	c1m
c21	c22	…	c2m
…	…	…	…
cn1	cn2		cnm

Целевая функция, которую следует минимизировать, записы­вается как:

Z = c₁₁*x₁₁ + c₁₂*x₁₂ + … + c₁m*x₁m + c₂₁*x₂₁ + c₂₂*x₂₂ + … + c₂m*x₂m + …

+ cnm*xnm

Ограничения для разных типов транспортной задачи будут выглядеть следующим образом:

1. Ограничения для сбалансированной задачи

Для сбалансированной задачи сумма грузов хi1+ xi2+ ... + xim, отправленных из любого пункта отправления Оi, должна равняться запасу грузов аi, в этом пункте отправления.

Отсюда получаем п ограничений в виде равенств:

x₁₁ + x₁₂ + … + x₁m = a₁

x₂1 + x₂₂ + … + x₂m = a₂

…

xn₁ + xn₂ + … + xnm = an

Аналогично, сумма грузов, полученных в любом пункте назначения Нj, должна равняться объему грузов bj,заказан­ных в этом пункте назначения.

- Получаем еще т ограничений в виде равенств:

x₁₁ + x₂₁ + … + xn₁ = b₁

x₁₂ + x₂₂ + … + xn₂ = b₂

…

x_1m + x_2m + … + x_nm = b_m

Итак, математическая модель для сбалансированной транспорт­ной задачи построена: имеется пт переменных xij,целевая функция, которую необходимо минимизировать, и п + т ограничений в виде равенств, а также условия неотрицательности для переменных.

2. Ограничения для задачи с дефицитом

Для несбалансированной задачи с дефицитом спрос в пунктах назначения превышает предложения пунктов отправления, т.е выполняется неравенство: сумма аi < суммы bj. В этих условиях груз из пунктов отправления будет вывезен полностью, но некоторые пункты назначения недополучат заказанные грузы.

Следовательно, ограничения, определяющие вывоз грузов из пунктов отправления, надо задать в виде равенств, а ограничения, определяющие объем грузов, поступающих в пункты назначения, надо задать в виде неравенств.

Имеем п ограничений в виде равенств:

x₁₁ + x₁₂ + … + x_1m = a₁

x₂₁ + x₂₂ + … + x_2m = a₂

…

x_n1 + x _n2 + … + x_nm = a_n

Получаем еще т ограничений в виде неравенств:

x₁₁ + x₂₁ + … + x_n1 <= b₁

x₁₂ + x₂₂ + … + x_n2 <= b₂

…

x_1m + x_2m + … + x_nm <= b_m

3. Ограничения для задачи с избытком

В несбалансированной задаче с избытком предложения пунктов отправления превышают спрос в пунктах назначения. Следовательно, груз в пунктах назначения будет получен полностью, но в некоторых пунктах отправления останется часть не вывезенных грузов. Поэтому ограничения, опpеделяющие вывоз грузов из пунктов отправления, надо задать в виде неравенств, а ограничения, определяющие объем грузов, поступающих в пункты назначения, надо задать в виде равенств.

Имеем n ограничений в виде неравенств:

x₁₁ + x₁₂ + … + x_1m <= a₁

x₂₁ + x₂₂ + … + x_2m <= a₂

…

x_n1 + x_n2 + … + x_nm <= a_n

Получаем еще т ограничений в виде равенств:

x₁₁ + x₂₁ + … + x_n1 = b₁

x₁₂ + x₂₂ + … + x_n2 = b₂

…

x_1m + x_2m + … + x_nm = b_m

В отличие от других линейных задач оптимизации, в транспортных задачах можно гарантировать целочисленность решения, если целыми числами выражаются запасы грузов аi. в пунктах отправления и заявки на гру­зы bj. в пунктах назначения.

Задание 1

Фирма Турлюкс имеет свои представительства в городах Москва, Минск и Киев. У фирмы есть клиенты (300, 100 и 250 человек соответственно), желающие посетить один из городов Казань, Рига, Воронеж, Курск, Владимир.

В соответствии с договорами, эти города могут принять 200, 100, 150, 150, 50 человек соответственно. Стоимости проезда (руб.) из пунктов отправления в пункт назначения на одного человека сведены в таблицу:

Таблица 9

	Казань	Рига	Воронеж	Курск	Владимир
Москва
Минск
Киев

Распределить туристов по городам таким образом, чтобы затраты на проезд были минимальными. Для решения задачи воспользоваться надстройкой Поиск решения.

Ход выполнения работы

1. Запишите математическую модель для сбалансированной задачи и представьте ее в виде табличной модели Excel, рис.32. Для этого:

• неизвестное распределение туристов по городам обозначьте через 1.
• В ячейку D19 запишите целевую функцию:

=СУММПРОИЗВ (C4:G6;C12:G14);

• В ячейки Bi:

=СУММ (Ci:Gi)

• В ячейки C7:G7

=СУММ (C4:C6) : СУММ (G4:G6)

• В ячейки C24:G27:

=C4*C12 : G6*G14

Запустите надстройку Поиск решения, для чего откройте вкладку Данные и нажмите кнопкуПоиск решения.

2. В открывшемся окне Параметры поиска решения, рис.33, укажите адрес целевой ячейки, которую необходимо минимизировать и адреса диапазона изменяемых ячеек.

3. В поле ограничений запишите соответствующие ограничения, используя кнопку Добавить:

$B$4:$B$6 = $I$4:$I$6

$C$7:$G$7 = $C$9:$G$9

4. Нажмите кнопку Найти решение. В открывшемся окне Результаты поиска решения подтвердите сохранение найденного решения.

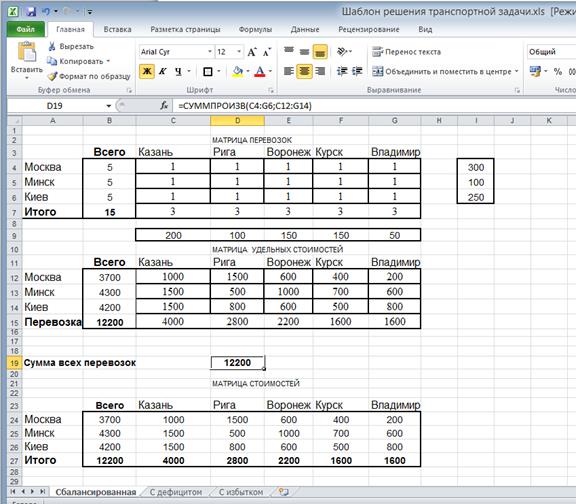
Рис.32

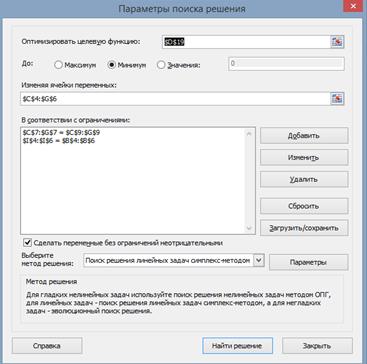
Рис.33

Задание 2

Решите самостоятельно предыдущую задачу для случаев несбалансированной задачи с дефицитом, когда клиенты (300, 100 и 250 человек) желают посетить города, которые могут принять 250, 150, 200, 150 и 100 человек соответственно.

Задание 3

Решите самостоятельно предыдущую задачу для случаев несбалансированной задачи с избытком, когда клиенты (300, 100 и 250 человек) желают посетить города, которые могут принять 150, 50, 150, 100 и 25 человек соответственно.

Анализ безубыточности

В анализе безубыточности оцениваются финансовые средства, необходимые для организации начала производства, и средства, вкладываемые в производство новой продукции, до тех пор, пока финансовые показатели не выйдут на точку безубыточности. Точка безубыточности характеризуется тем, что суммарный доход от реализации новой продукции равняется суммарным затратам на ее производство плюс начальные вложения. В непроизводственной сфере, например, в торговле или индустрии услуг, точка безубыточности имеет еще одно название — порог рентабельности.

Пусть предприятие планирует начать выпуск n новых видов изделий И₁, И₂, ..., И_n. Для организации выпуска изделий каждого виданеобходимы начальные вложения в₁, в₂,..., в_nсоответственно. Это так называемые фиксированные, или постоянные, затраты, которые независят от количества изготовляемых в будущем изделий (в эти за­траты обычно входят покупка, установка и наладка нового оборудова­ния, отладка технологических процессов, заем и обучение персонала и т.п.). При производстве каждого типа изделий предприятие также несет переменные затраты.

Пусть з₁, з₂, ..., з_n– переменныезатраты на производство одной единицы каждого вида изделия И₁, И₂, ..., И_n., а с₁, с₂,..., с_n – цена продажи для каждого вида изделия. Это – минимальный набор дан­ных, необходимый для проведения анализа безубыточности.

Исходя из определения точки безубыточности, уравнение безубыточности, как равенство доходов и затрат (включая фиксированные затраты), имеет следующий вид:

∑c_i*x_i = ∑з_i*x_i + ∑в_i,

где xi – количество изделий каждого вида, при котором достигается точка безубыточности.

Это уравнение можно переписать в виде:

∑(c_i-з_i)*x_i = ∑в_i

В случае многих видов изделий это уравнение имеет бесконечно много решений, поэтому в таких задачах, кроме уравнения безубыточности, вводятся дополнительные условия. Чаще всего вводится условие минимума переменных затрат для достижения точки безубыточности или условие максимума дохода (прибыли), полученного для достижения точки безубыточности. В первом случае целевая функция, которую необходимо минимизировать, имеет вид:

Z = ∑з_i*x_i

Во втором случае целевая функция, которую необходимо максимизировать, имеет вид:

Z = ∑c_i*x_i

В качестве ограничения имеем уравнение безубыточности:

∑(c_i-з_i)*x_i = ∑в_i

В реальных задачах вводятся дополнительные условия (ограничения), вытекающие, например, из ограниченности производственных мощностей или ограниченности ресурсов, либо потребностей рынка.

Задание 1

Фирма Турлюкс планирует разработать 3 новых тура в:

• Турцию;
• Испанию;
• Тунис.

Соответствующие данные о затратах и доходах на плановый период представлены в таблице 10.

Таблица 10

Туры	Планируемая стоимость тура на 1 человека, руб	Переменные затраты на одного человека, руб	Фиксированные затраты, руб
Турция Испания Тунис	50 000 60 000 55 000	5 000 6 000 5 500	10 000 000 15 000 000 12 000 000

Определить количество туристов, которых надо отправить в эти страны, при которых фирма выходит на точку безубыточности. Следует отметить, что фирма заключила договора на поставку 300 туристов в Турцию и 200 туристов в Испанию и руководство заинтересовано в обязательном выполнении этих договоров. Кроме того, анализ рынка, проведенный отделом маркетинга, свидетельствует, что рынок не может «поглотить» более 400 туристов в Тунис.

Ход выполнения работы

1. Запишите математическую модель для уравнения безубыточности задачи и представьте ее в виде табличной модели Excel, рис.34.

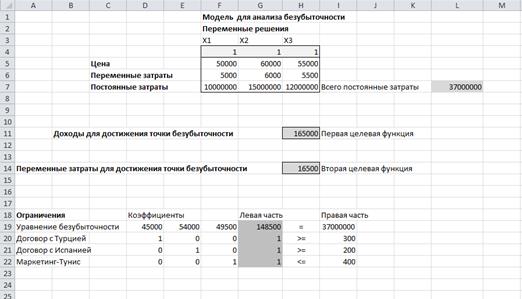
Рис.34

Для этого:

· неизвестное количество туристов для каждой из стран, при котором фирма выходит на точку безубыточности, обозначьте через 1 (ячейки F4:G4).

· Заполните ячейки F5:H7 согласно таблице 10.

• В ячейке H11 запишите целевую функцию:

=СУММПРОИЗВ (F4:H4;F5:H5)

• В ячейке H14 запишите целевую функцию:

=СУММПРОИЗВ (F4:H6;F5:H6)

• В ячейке L7:

=СУММ (F7:H7)

2. Определите ограничения для данной задачи. Ограничений должно быть 4 (одно ограничение вытекает из уравнения безубыточности). Для этого:

• Заполните ячейки D19:F19, записав в них, соответственно, разности:

=F5 - F6

=G5 - G6

=H5 - H6

• В ячейке G19 запишите левую часть уравнения безубыточности:

=D19*F4 + E19*G4 + F19*H4

• В ячейке I19 запишите правую часть уравнения безубыточности:

=L7

(в результате решения уравнения безубыточности содержимое ячеек G19 и I19 должно быть равно)

• Заполните ячейки D20, E21,F22, записав в них соответственно:

=F4, =G4, =H4

• Заполните ячейки G20:G22, записав в них соответственно:

=СУММ (D20:F20)

=СУММ (D21:F21)

=СУММ (D22:F22)

3. Определите точку безубыточности, исходя из условия максимизации дохода. Для этого:

• запустите надстройку Поиск решения, открыв вкладку Данные и нажав кнопку – Поиск решения.
• В открывшемся окне Параметры поиска решения, рис.35, укажите адрес целевой ячейки H11, которую необходимо максимизировать и адреса диапазона изменяемых ячеек F4:H4.
• В поле ограничений запишите соответствующие ограничения, рис.35, используя кнопку Добавить.
• Нажмите кнопку Найти решение. В открывшемся окне Результаты поиска решения подтвердите сохранение найденного решения.

1. Определите точку безубыточности, исходя из условия минимизации затрат при достижении точки безубыточности. Сравните результаты.

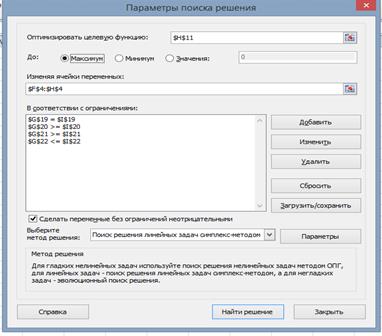
Рис.35

Список литературы

1. Уокенбах[П1] [П2] [П3] . Microsoft Excel 2010. Библия пользователя. – М.:Диалектика, 2014. - 912 с.
2. Минько А.А. Принятие решений с помощью Excel.- М.: Эксмо, 2007. - 240 с.

3. Решение прикладных задач менеджмента гостеприимства в Excel: Учебно-методическое пособие по курсу «Информатика». Под общей ред. Цикина В.П. – М.: ООО «А-Пресс Дизайн», 2005.

[П1]

[П2]

[П3]