V. Риск инвестиционного портфеля

Чаще всего инвестор работает не с отдельным активом, а с некоторым их набором, называемым портфелем ценных бумаг, или инвестиционным портфелем.

Оценивая риск конкретного актива из инвестиционного портфеля, можно действовать двояко: либо рассматривать этот актив изолированно от других активов, либо считать его неотъемлемой частью портфеля. Оказывается, что оценка рискованности актива и целесообразности операции с ним могут меняться. Более того, актив, имеющий высокий уровень риска при рассмотрении его изолированно, может оказаться практически безрисковым с позиции портфеля – при определённом сочетании входящих в этот портфель активов. Например, теоретически можно подобрать два финансовых актива, каждый из которых имеет высокий уровень риска, но которые, будучи объединенными вместе, составят абсолютно безрисковый портфель.

При оценке портфеля и целесообразности операций с входящими в него активами, необходимо оперировать показателями доходности и риска портфеля в целом.

Доходность портфеля (k_p) представляет собой линейную функцию показателей доходности входящих в него активов и может быть рассчитана по формуле средней арифметической взвешенной (в данном случае речь может идти как об ожидаемой, так и о фактической доходности):

, (4.20)

где k_j – доходность j-го актива;

d_j – доля j-го актива в портфеле;

n – число активов в портфеле.

Как и в случае с отдельными активами, мерой риска портфеля служит вариация его доходности, взаимосвязь между риском портфеля и риском входящих в него активов носит более сложный характер и не описывается формулой средней арифметической.

В частности, если в качестве меры риска выбрано среднее квадратическое отклонение, то его значение для портфеля, содержащего k активов, может быть определено по уравнению:

, (4.21)

где d_i – доля i-го актива в портфеле;

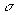_i – вариация доходности i-го актива;

r_ij – коэффициент корреляции между ожидаемыми доходностями i-го и j-го активов.

Ситуация осложняется при переходе к портфелям с большим числом входящих в них активов. В этом случае возникает ряд проблем как теоретического, так и вычислительного характера.

Во-первых, в ситуации с портфелем риск, ассоциированный с каким-то конкретным активом, не может рассматриваться изолированно.

Во-вторых, поскольку, все финансовые инвестиции различаются по уровню доходности и риска, их возможные сочетания в портфеле усредняют эти количественные характеристики, а в случае оптимального их сочетания можно добиться значительного снижения риска финансового инвестиционного портфеля.

В-третьих, приемлемая доходность не может быть достигнута простым отбором наиболее доходных активов, поскольку обычно приводит к увеличению риска портфеля.

В-четвёртых, вариация доходности имеет место не только в пространстве, но и динамике, т.е. тенденции доходности двух случайно выбранных из портфеля активов вовсе не обязательно совпадают, более того, они могут быть разнонаправленными.

В-пятых, в условиях множественности входящих в портфель активов существенно усложняются вычислительные процедуры.

Вопросы для контроля

1. Основные теории оценки ценных бумаг?

2. Способы выплат доходов по облигациям?

3. Стоимостные показатели облигаций?

4. Доходность акций?

5. Концепция риска и методы его оценки?

6. Риск инвестиционного портфеля?