Предельная норма предпочтений во времени. Двухвершинный и одновершинный профили.

Коробка Эджуорта в двухсубъектной двухпродуктовой модели. Зона добровольного обмена

С помощью диаграммы (или коробки) Эджуорта рассматриваются эффективные варианты распределения потребительских благ. Коробка Эджуорта представляет собой прямоугольник, в котором левый нижний угол является началом системы координат субъекта А, а верхний правый угол -началом системы координат субъекта В.

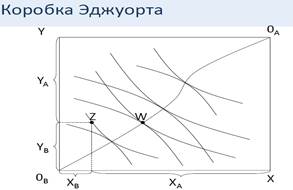
Z - начальное распределение благ X и Y. На графике показаны кривые безразличия участников А и В. Линия, которая на диаграмме Эджуорта соединяет точки А и В, называется контрактной кривой.

Модель Коробки Эджуорта может быть применена для анализа производства. Предположим, производиться два продукта X и Y, при использовании факторов K1 и L1, K2 и L2, соответственно. Вместо кривых безразличия, в этой модели используются изокванты, каждая из которых представляет определенный объем выпуска блага X и Y.

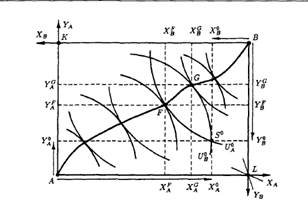
Коробка Эджуорта, изображена на рис.. Она представляет совмещенные карты безразличия двух субъектов, А та. В, причем карта безразличия В повернута на 180°, так что начала координат каждой из двух карт безразличия становятся противолежащими вершинами прямоугольника — коробки (А, В).

Любая точка в пределах коробки Эджуорта характеризует некоторое распределение двух благ, X и У, между двумя субъектами, А и В. Пусть, например, точка S° на рис. будет точкой изначального распределения благ X и У между А и В.

Тогда субъект А получит набор S^(X°^,Y°), а субъект В — набор

8% (Xg,Yg). При этом все наличное количество благ X и У будет без остатка распределено между ними, так что

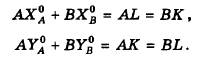
Коротко выводы:

1. Если в точке, характеризующей в коробке Эджуорта изначальное распределение двух благ, кривые безразличия двух индивидов пересекаются (а не касаются одна другой), обмен благами может способствовать достижению каждым субъектом более высокого уровня удовлетворения (полезности).

2. Конечное распределение двух благ между двумя индивидами соответствует точке пересечения их кривых предложения, которая в то же время является и точкой касания их кривых безразличия и лежит на контрактной кривой.

3. В этой точке достигнутого в процессе обмена равновесия предельные нормы замены двух благ для обоих субъектов одинаковы и равны соотношению цен:

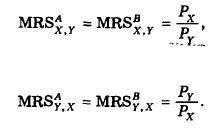
Предельная норма предпочтений во времени. Двухвершинный и одновершинный профили.

Тех, кто предпочитает настоящее потребление будущему, можно назвать нетерпеливыми. Однако при достаточно малом объеме текущего потребления в сравнении с объемом будущего потребления у большинства людей предельная норма предпочтения во времени будет высокой (обычно кривые безразличия на своих левых верхних участках имеют крутой наклон). Поэтому, чтобы классифицировать потребителей по степени нетерпеливости, следует поинтересоваться их предельными нормами предпочтения во времени при условии равенства объемов настоящего и будущего потребления.

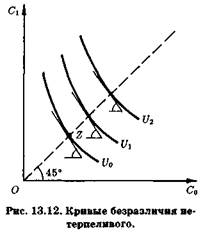
Рассмотрим на кривой безразличия U0 (рис. 13.12) точку Z, которая лежит на луче, проведенном из начала координат под углом 45°. В этой точке текущее потребление в точности равно будущему потреблению. Заметим, что предельная норма предпочтения во времени в точке Z у данного потребителя больше единицы. Следовательно, когда его настоящее и будущее потребление равны, нужно увеличить будущее потребление данного субъекта более чем на 1 руб., чтобы он отказался от текущего потребления тоже на 1 руб. Такого потребителя можно назвать нетерпеливым: его предельная норма предпочтения во времени на луче, проходящем под углом 45°, больше единицы.

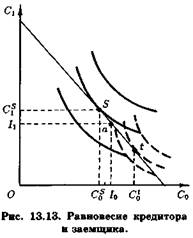
Равновесная (оптимальная) программа потребления определяется, как всегда, из требования максимизации полезности при заданном бюджетном ограничении. На рис. 13.13 изображены бюджетное ограничение Федора и его карта безразличия (сплошные кривые). Федор достигает максимума полезности в точке S. В этой точке кривая безразличия касается бюджетной линии, следовательно,

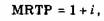
где i — ставка процента, по которой возможно давать и брать деньги в кредит.

В равновесии текущее потребление Федора С§ меньше текущего дохода /0, а будущее потребление Су больше будущего дохода Jj. Следовательно, Федор является кредитором (заимодавцем).

Пусть Трифон наделен такими же доходами в настоящем и будущем, как и Федор, и пользуется той же ставкой процента на финансовом рынке. Но карта безразличия у Трифона другая, она представлена на рис. 13.13 прерывистыми кривыми. Равновесие Трифона характеризуется точкой t, он берет взаймы в настоящем периоде и сокращает потребляемую часть в доходе будущего периода. Он в отличие от Федора является заемщиком.

Предпочтения членов семьи относительно трех телепередач (ТВ-1, ТВ-2, ТВ-3)

Член семьи	Предпочтения
A B C	TB-1>TB-2>TB-3 TB-2>TB-3>TB-1 TB-3>TB-1>TB-2

Представим теперь, что все трое попытаются исходя из своих индивидуальных предпочтений построить функцию семейной (что в этом примере тождественно общественной) полезности. При выборе между ТВ-1 и ТВ-2 большинство (А и С) выскажется в пользу ТВ-1. При выборе между ТВ-2 и ТВ-3 большинство (А и В) выскажется в пользу ТВ-2. Значит, исходя из аксиомы транзитивности индивидуальных предпочтений (раздел 3.2), мы вправе предположить, что если ТВ-1 > ТВ-2, а ТВ-2 > ТВ-3, то и ТВ-1 > TB-З. Но в нашем примере дело обстоит явно наоборот. При выборе между ТВ-1 и ТВ-3 большинство (В и С) выскажется в пользу ТВ-3. Таким образом, хотя ТВ-1 >-> ТВ-2, а ТВ-2 х ТВ-3, ТВ-3 > ТВ-1! Таким образом, аксиома транзитивности здесь не выполняется. В результате голосование носит циклический характер, что и составляет содержание парадокса.

Из-за нетранзитивности коллективных предпочтений общественный выбор будет зависеть от очередности постановки альтернатив на голосование. Если сначала выбирать между ТВ-1 и ТВ-2, а затем сравнивать выбранную альтернативу с ТВ-3, то наша семья выберет ТВ-3. Если же сначала выбирать между ТВ-3 и ТВ-1, а затем сравнивать выбранную альтернативу с ТВ-2, то предпочтение будет отдано ТВ-2. Зависимость коллективных решений от очередности постановки альтернатив на голосование открывает возможности для манипулирования "повесткой дня". Результат голосования зависит в этой ситуации от предусмотренного числа циклов (туров) голосования.

Предпочтения членов семьи относительно трех телепередач (ТВ-1, ТВ-2, ТВ-3)

Член семьи	Предпочтения
A B C	TB-1>TB-2>TB-3 TB-2>TB-3>TB-1 TB-3>TB-1>TB-2

Представим теперь, что все трое попытаются исходя из своих индивидуальных предпочтений построить функцию семейной (что в этом примере тождественно общественной) полезности. При выборе между ТВ-1 и ТВ-2 большинство (А и С) выскажется в пользу ТВ-1. При выборе между ТВ-2 и ТВ-3 большинство (А и В) выскажется в пользу ТВ-2. Значит, исходя из аксиомы транзитивности индивидуальных предпочтений (раздел 3.2), мы вправе предположить, что если ТВ-1 > ТВ-2, а ТВ-2 > ТВ-3, то и ТВ-1 > TB-З. Но в нашем примере дело обстоит явно наоборот. При выборе между ТВ-1 и ТВ-3 большинство (В и С) выскажется в пользу ТВ-3. Таким образом, хотя ТВ-1 >-> ТВ-2, а ТВ-2 х ТВ-3, ТВ-3 > ТВ-1! Таким образом, аксиома транзитивности здесь не выполняется. В результате голосование носит циклический характер, что и составляет содержание парадокса.

Из-за нетранзитивности коллективных предпочтений общественный выбор будет зависеть от очередности постановки альтернатив на голосование. Если сначала выбирать между ТВ-1 и ТВ-2, а затем сравнивать выбранную альтернативу с ТВ-3, то наша семья выберет ТВ-3. Если же сначала выбирать между ТВ-3 и ТВ-1, а затем сравнивать выбранную альтернативу с ТВ-2, то предпочтение будет отдано ТВ-2. Зависимость коллективных решений от очередности постановки альтернатив на голосование открывает возможности для манипулирования "повесткой дня". Результат голосования зависит в этой ситуации от предусмотренного числа циклов (туров) голосования.

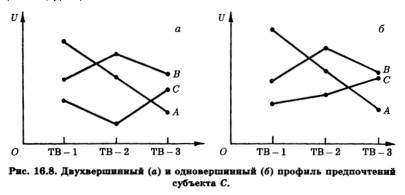
Причиной нерационального исхода голосования в нашем примере явился так называемый двухвершинный профиль предпочтений субъекта С, что очевидно из рис. 16.8, а. Если бы этот профиль имел одну вершину (рис. 16.8, б), т. е. если бы предпочтения С были бы такими, как в табл. 16.3, то выбор семьи был бы определен и рационален. В каком бы порядке ни ставились в этом случае на голосование альтернативы, его результатом будет выбор ТВ-2. Так, если сначала выбор будет осуществляться между ТВ-1 и ТВ-2, то голосами В и С поддержку получит ТВ-2, а затем при сравнении ТВ-2 и ТВ-3 голосами А и В будет выбрано ТВ-2. Если же сначала будут сравниваться ТВ-2 и ТВ-3, а затем выигравшая альтернатива будет сопоставляться с ТВ-1, то голосами В и С также будет выбрано ТВ-2. Результат не изменится и в том случае, если, отбросив самую непопулярную альтернативу ТВ-1, сравнить ТВ-2 и ТВ-3. Здесь независимо от очередности голосования его исход определится предпочтениями медианного субъекта В. Как видно на рис. 16.8, б, именно они находятся посередине между предпочтениями А и С.

Причиной нерационального исхода голосования в нашем примере явился так называемый двухвершинный профиль предпочтений субъекта С, что очевидно из рис. 16.8, а. Если бы этот профиль имел одну вершину (рис. 16.8, б), т. е. если бы предпочтения С были бы такими, как в табл. 16.3, то выбор семьи был бы определен и рационален. В каком бы порядке ни ставились в этом случае на голосование альтернативы, его результатом будет выбор ТВ-2. Так, если сначала выбор будет осуществляться между ТВ-1 и ТВ-2, то голосами В и С поддержку получит ТВ-2, а затем при сравнении ТВ-2 и ТВ-3 голосами А и В будет выбрано ТВ-2. Если же сначала будут сравниваться ТВ-2 и ТВ-3, а затем выигравшая альтернатива будет сопоставляться с ТВ-1, то голосами В и С также будет выбрано ТВ-2. Результат не изменится и в том случае, если, отбросив самую непопулярную альтернативу ТВ-1, сравнить ТВ-2 и ТВ-3. Здесь независимо от очередности голосования его исход определится предпочтениями медианного субъекта В. Как видно на рис. 16.8, б, именно они находятся посередине между предпочтениями А и С.