Оценка адекватности модели

Если модель не учитывает существенную закономерность исследуемого процесса, ее нельзя применять для анализа и прогнозирования.

Модельсчитается адекватной, если ряд остатков обладает свойствами:

o независимость;

o их случайность;

o соответствие нормальному закону распределения;

o равенство нулю средней ошибки.

Наличие этих свойств проверяется с определенной степенью уверенности в правильности выводов. На практике обычно используется 5%- ный уровень значимости, соответствующий уверенности в 95%.

При проверке независимости (отсутствии автокорреляции) определяется отсутствие в ряду остатков систематической составляющей. Это проверяется с помощью d - критерия Дарбина - Уотсона, в соответствии с которым вычисляется коэффициент d:

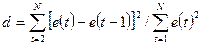
Вычисленная величина этого критерия сравнивается с двумя табличными уровнями: нижним - d1 и верхним - d2, значение которых зависит от количества наблюдений N, сложности модели (количества параметров) и выбранного уровня вероятности суждения. Если
d-коэффициент превышает 2, то это свидетельствует об отрицательной корреляции и перед входом в таблицу его величину надо преобразовать: d' = 4 - d.

Если 0 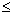d (или d') 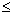d1 – модель неадекватна (уровни ряда остатков сильно автокоррелированы);

d2 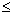d (или d') 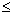2 – модель адекватна;

d1 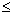d (или d') 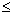d2 – однозначного вывода сделать нельзя и необходимо применять другие критерии (на основе коэффициента автокорреляции r(1), Q-коэффициента).

Надежным инструментом оценки независимости уровней ряда является автокорреляционная функция (АКФ), которая представляет собой последовательность коэффициентов автокорреляции. Если средний уровень ряда остатков равен нулю или другой малой величине, коэффициенты автокорреляции при сдвиге на m шагов вычисляются по простой формуле:

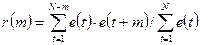
Вывод о независимости уровней можно сделать на основе первого коэффициента автокорреляции r(1), вычисленного по этой формуле при m=1. Если r(1) > r_табл, то присутствие в остаточном ряду существенной автокорреляции подтверждается – модель адекватна.

Целесообразно анализировать и другие значения АКФ. На основе всех коэффициентов, количество которых (М) не должно превышать одной трети объема данных, рассчитывается коэффициент Q:

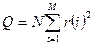
Эта статистика, имеющая распределение χ-квадрат с (N-M-1) степенями свободы, не должна превышать соответствующего табличного уровня.

Рассмотренные три критерия в совокупности (коэффициент d, коэффициент автокорреляции r(1) и коэффициент Q) позволяют однозначно определить независимость уровней ряда.

Для проверки случайности уровней ряда могут быть использованы критерий серий и критерий поворотных точек. Среди модификаций критерия серий наиболее удачной с точки зрения соотношения между сложностью и надежностью, на наш взгляд, является критерий «восходящих» и «нисходящих» серий. По результатам сравнения двух последних уровней ряда остатков составляется последовательность из нулей и единиц. Если E(t+1) - E(t) > 0, в последовательности ставиться ноль, в противном случае – единица. Если исходный ряд представляет собой случайную последовательность, то продолжительность самой длинной серии τ(N), т.е. последовательности, состоящей из идущих подряд нулей или единиц, должна быть небольшой, а общее число серий v – малым. Ряд остатков считается случайным с 95%-ной вероятностью в случае выполнения двух неравенств:

τ(N) < τ₀(N)

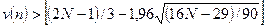
Квадратные скобки здесь означают, что от результата вычислений берется целая часть числа (не путать с процедурой округления!). Критическое значение длины серии τ₀ = 5; при 26 < N < 153, τ₀ = 6; а при N > 153, τ₀ = 7.

Менее строгим является критерий поворотных точек, который называется также критерием “пиков” и “впадин”. В соответствии с этим критерием каждый уровень ряда сравнивается с двумя соединенными с ними. Если он больше или меньше их, то эта точка считается поворотной. Далее подсчитывается сумма поворотных точек р. В случайном ряду чисел должно выполняться строгое неравенство:

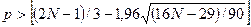
Соответствие ряда остатков нормальному закону распределения важно с точки зрения правомерности построения доверительных интервалов прогноза. Наиболее существенными свойствами ряда отклонений являются их симметричность относительно модели и преобладание малых по абсолютной величине ошибок над большими. В этой связи определяется близость к соответствующим параметрам нормального закона распределения коэффициентов асимметрии – A_c (мера скошенности) и эксцесса Э_к (мера «скученности») наблюдений около модели:

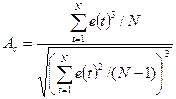
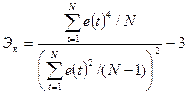
Если эти коэффициенты приблизительно равны нулю, то ряд остатков распределен в соответствии с нормальным законом. Для оценки степени их близости к нулю вычисляются дисперсии:

S_a = 6 (N - 2) / (N + 1) / (N + 3)

S_э = 24N (N - 2)(N - 3)/ (N + 1)/(N + 3) / (N + 5)

Если вычисленные абсолютные значения этих коэффициентов не превосходят полутора среднеквадратических отклонений, то считается, что распределение ряда остатков не противоречит нормальному закону. Если хотя бы один из них превышает удвоенную величину среднеквадратического отклонения, то распределение ряда не соответствует нормальному закону, а построение доверительных интервалов неправомочно. В случае попадания в зону неопределенности (между полутора и двумя СКО) используются другие критерии, частности RS- критерий:

RS = (E_max - E_min) / S,

где E_max – максимальный уровень ряда остатков;

E_min – минимальный уровень ряда остатков;

S – среднее квадратическое отклонение.

Если значение этого критерия попадает между табулированными границами с заданным уровнем вероятности, то гипотеза о нормальном распределении ряда остатков принимается. (Для N = 10 и 5%-ного уровня значимости этот интервал равен 2,7 - 3,7).

Равенство нулю средней ошибки (математическое ожидание случайной последовательности) проверяют с помощью t-критерия Стьюдента:

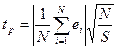
Гипотеза отклоняется, если расчетное значение t_p больше табличного уровня t-критерия с (N - 1) степенями свободы и выбранным уровнем значимости.

Оценка точности модели

В статистическом анализе известно большое число характеристик точности. Наиболее часто в практической работе, кроме среднеквадратического отклонения, используются:

o максимальная по абсолютной величине ошибка:

E_max = max|e(t)|;

o относительная максимальная ошибка:

Е_отн = Е_max / Y_ср * 100%

o средняя по модулю ошибка:

|Е_ср| = (e(1) + ... + e(N))/N

o относительная средняя по модулю ошибка:

|Е_ср|_отн= |Е_ср| / Y_ср * 100%

Эти показатели дают представление об абсолютной величине ошибки модели и о доле ошибки в процентном отношении к среднему значению результативного признака.

При использовании ретропрогноза – подхода, когда несколько последних уровней ряда оставляются в качестве проверочной последовательности – точность прогнозных оценок определяется на основе этих же показателей.

Лучшей по точности считается та модель, у которой все перечисленные характеристики имеют меньшую величину. Однако эти показатели по-разному отражают степень точности модели и потому нередко дают противоречивые выводы. Для однозначного выбора лучшей модели исследователь должен воспользоваться либо одним основным показателем, либо обобщенным критерием.

Примечание.

Для расширенной характеристики модели регрессии вычисляется несколько дополнительных показателей.

Кроме рассмотренных выше характеристик, целесообразно использовать корреляционное отношение (индекс корреляции) R, а также характеристики существенности модели в целом и отдельных ее коэффициентов:

,

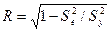где S_e² – сумма квадратов уровней остаточной компоненты;

S_y² – сумма квадратов отклонений уровней исходного ряда от его среднего значения.

Данный коэффициент является универсальным, так как он отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной модели и их линейной зависимости он равен коэффициенту линейной корреляции.

Коэффициент множественной корреляции (индекс корреляции), возведенный в квадрат, называется коэффициентом детерминации.

Рассмотрим, к примеру, ситуацию, когда коэффициент корреляции между объемом выручки от реализации и расходами на рекламу составляет 0.8. Таким образом, r =0.8, а коэффициент детерминации r*r = 0.64 ( =64% ). Следовательно, это показывает, что 64 % изменений в объеме реализации можно объяснить изменениями в расходах на рекламу. Такой способ описания зависимости между двумя переменными подводит к рассмотрению причины и следствия. Из двух анализируемых переменных одна является прчиной (x), а другая – следствием (y). Например, надежды возлагаются на то, что реклама вызовет изменение объема реализации. Таким образом, мы можеж сказать, что расходы на рекламу являются «причиной», а объем реализации – «следствием». Рассмотрим вероятную ситуацию, при которой коэффициент корреляции между двумя переменными составляет +1. Итак, r = +1, а коэффициент детерминации r*r = 1. Это подразумевает, что 100% изменений в объеме реализации вызваны изменениями в расходах на рекламу. В таком случае изменения в расходах на рекламу автоматически вызывают пропорциональные изменения в объемах реализации, что для любого руководителя службы маркетинга ситуация идеальна. На практике, конечно, крайне маловероятно, что степень корреляции будет столь идеальной. Даже когда зависимость между двумя переменными зависима, требуется учет множества других факторов. Так, для примеров такого рода вполне обычным значением коэффициента детерминации будет показатель в диапазоне от 0.1 до 0.3. Например, коэффициент детерминации, равный 0.2 (20%),показывает, что 20% изменений в объеме реализации вызван изменениями в расходах на рекламу. Во многих хозяйственных ситуациях 20%-ный результат служит более чем адекватным обоснованием необходимости продолжать рекламирование. При истолковании значений коэффициента корреляции и коэффициента детерминации следует проявлять осторожность. Существует вероятность получения очень высоких значений коэффициента корреляции при отсутствии какой-либо прямой зависимости между двумя рассматриваемыми переменными. Рассмотрим, например, следующую ситуацию, когда мы имеем для анализа собранные за 10 лет данные по стоимости экспорта из Великобритании и средней цене стиральных машин во Франции:

Год
Экспорт
Цена	1,5	1,6	1,9	2,0	2,5	2,5	2,6	2,9	3,0	3,5

Данные переменные были отобраны ввиду фактического отсутствия прямой зависимости между ними. Итак, можно вычислить коэффициент корреляции между этими двумя переменными при x – стоимости экспорта из Великобритании и y – цене стиральных машин во Франции. Коэффициент корреляции составляет r = 0,9635. Таким образом, коэффициент детерминации r*r = 0,928 = 92,8 %

Такой коэффициент детерминации, видимо, указывает на то, что 92,8% изменений в цене стиральных машин во Франции вызваны колебаниями в стоимости экспорта из Великобритании. Такая зависимость называется ложной, так как прямая зависимость между переменными, очевидно, незначительна. Коэффициент корреляции оказывается значимым в этом случае по той причине, что обе переменные связаны с третьей переменной, т.е. с временным периодом. Такое следствие часто встречается при анализе экономических данных, взятых за длительный период времени, поскольку важным фактором здесь может быть инфляция. Чтобы установить наличие истинной зависимости между двумя переменными, необходимо устранить элемент инфляции при рассмотрении этих переменных и заново вычислить корреляцию. Выше приведенный пример представляется несколько более сложным, так как уровень инфляции в разных странах может быть неодинаков. Однако в целом между двумя значениями уровня инфляции вероятно существование зависимости, что и может дать ложную корреляцию между различными финансовыми и экономическими показателями, взятыми за продолжительный период времени.

Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий при интерпретации применяются средние частные коэффициенты эластичности Э(j) и бета-коэффициенты β(j) , которые рассчитываются соответственно по формулам:

Э(j)=a(j)X_cp(j)/Y_cp

β(j)= a(j)S(j)/S_y,

где S(j) – среднеквадратическое отклонение фактора j.

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора j на один процент. Однако он не учитывает степень колеблемости факторов.

Бета-коэффициент показывает, на какую часть величины среднеквадратического отклонения меняется среднее значение зависимой переменной с изменением соответствующей независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных.

Указанные коэффициенты позволяют проранжировать факторы по степени влияния факторов на зависимую переменную.

Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициентов Δ(j):

Δ(j) = r(j) β(j) / R²,

где r(j) - коэффициент парной корреляции между фактором j (j=1,...,m) и зависимой переменной;

R² = r(1) * β(1)+r(2) * β (2)+..+r(m) * β (m)

При корректно проводимом анализе все β - коэффициентыположительны.