Процентные ставки и методы их начисления
Методические указания. Выделяют две схемы начисления процентов:
- простые проценты (предполагает неизменность базы начисления):
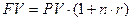, (9)
где n – период начисления процентов, лет;
r – годовая процентная ставка, %.
- сложные проценты (предполагается, что исчисление производится с величины, включающей ранее начисленные проценты):
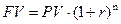. (10)
В финансовых расчетах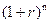 
называется мультиплицирующим множителем (приложение 1).
Эквивалентными процентными ставками называются любые две ставки из ниже перечисленных:
- простая процентная ставка наращения;
- сложная процентная ставка наращения;
- номинальная процентная ставка наращения;
- сила роста;
- простая учетная ставка;
- сложная учетная ставка, при замене одной на другую приводят к одинаковым финансовым результатам, т.е. отношения сторон не изменяются в рамках одной финансовой операции:
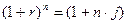, (10а)
где r – сложная процентная ставка наращения;
j – простая процентная ставка ращения;
n – период финансовой операции, лет.
Решив это равенство, получим:
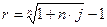, (10б)
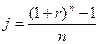(10в)
Для быстрой экономической оценки по схеме сложного наращения используется «правило 72-х»: если r процентная ставка, выраженная в % , то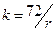 
представляет собой число периодов, за которое исходная сумма удвоится.
Взаимосвязь между простой и сложной схемой расчета представлена в таблице 1.
Таблица 1
Простая и сложная схемы наращения процента
| Период | Схема расчета @12% | Период | Схема расчета @12% | ||||
| месяц | ед. год. | простые | сложные | месяц | ед. год. | простые | сложные |
| 0,08 | 1,0100 | 1,0095 | 1,08 | 1,1300 | 1,1306 | ||
| 0,17 | 1,0200 | 1,0191 | 1,17 | 1,1400 | 1,1414 | ||
| 0,25 | 1,0300 | 1,0287 | 1,25 | 1,1500 | 1,1522 | ||
| 0,33 | 1,0400 | 1,0385 | 1,33 | 1,1600 | 1,1631 | ||
| 0,42 | 1,0500 | 1,0484 | 1,42 | 1,1700 | 1,1742 | ||
| 6 (полгода) | 0,50 | 1,0600 | 1,0583 | 18 (1,5 года) | 1,50 | 1,1800 | 1,1853 |
| 0,58 | 1,0700 | 1,0683 | 1,58 | 1,1900 | 1,1965 | ||
| 0,67 | 1,0800 | 1,0785 | 1,67 | 1,2000 | 1,2079 | ||
| 0,75 | 1,0900 | 1,0887 | 1,75 | 1,2100 | 1,2194 | ||
| 0,83 | 1,1000 | 1,0990 | 1,83 | 1,2200 | 1,2309 | ||
| 0,92 | 1,1100 | 1,1095 | 1,92 | 1,2300 | 1,2426 | ||
| 12 (1 год) | 1,00 | 1,1200 | 1,1200 | 24 (2 года) | 2,00 | 1,2400 | 1,2544 |
Как видно из таблицы 1, с позиции кредитора более выгодной является:
- схема простых процентов, если срок займа/кредита составляет до 1 года;
- схема сложных процентов, если срок займа/кредита составляет свыше 1 года;
- обе схемы дают одинаковый результат, если срок займа/кредита 1 год.
Пример. Инвестору предлагается разместить сумму 2050 тыс. руб. на депозите банка (12 % в год). Определите величину возвращаемой суммы (FV) на условиях начисления простых и сложных процентов, если периоды наращения суммы: а) 2 месяца; б) 10 месяцев; в) 1 год; г) 1,5 года; д) 2 года. Какой вариант начисления выгоден для инвестора? Через какой период удвоится исходная сумма?
Решение. Для исчисления простых процентов используем формулу (9):
а) 2 месяца или 0,17 года
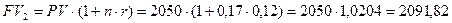тыс. руб.;
б) 10 месяцев или 0,83 года
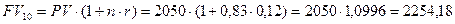тыс. руб.;
в) 12 месяцев или 1 год
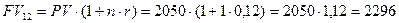тыс. руб.;
г) 18 месяцев или 1,5 года
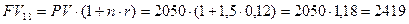тыс. руб.;
д) 24 месяца или 2 года
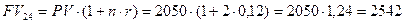тыс. руб.
Для исчисления сложных процентов используем формулу (10):
а) 2 месяца или 0,17 года
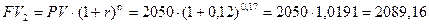тыс. руб.;
б) 10 месяцев или 0,83 года
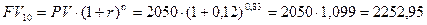тыс. руб.;
в) 12 месяцев или 1 год
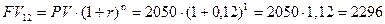тыс. руб.;
г) 18 месяцев или 1,5 года
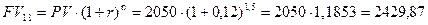тыс. руб.;
д) 24 месяца или 2 года
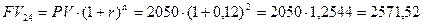тыс. руб.
С позиции инвестора более выгодной является:
- схема простых процентов, если срок займа/кредита составляет до 1 года;
- схема сложных процентов, если срок займа/кредита составляет свыше 1 года.
Исходная сумма удвоится через k=72/ r=72/12%≈6 лет.
Проверка: Период 6 лет или 72 месяца
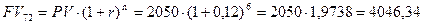тыс. руб.
Методические указания. На практике начисление процентов происходит несколько раз в год и за периоды времени не равные доле года, выраженной в месяцах, с этой целью используют формулы процентных начислений для расчета в днях:
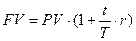, (11)
где t - продолжительность финансовой операции в днях;
T – количество дней в году.
Определяя период финансовой операции, принято день выдачи и день возврата денежных средств считать за один день (граничный день).
В зависимости от точности расчета финансовой операции и точности расчета продолжительности годовой базы выделяют четыре типа расчета:
1) Точные проценты (365 или 366) с точным числом дней финансовой операции, иначе «365/365»;
2) Точные проценты с приближенным числом дней финансовой операции (исходя из приближенной длительности месяца – 30 дней), иначе «365/360»;
3) Обыкновенные (коммерческие) проценты (продолжительность года 360 дней) с точным числом дней финансовой операции, иначе «360/365»;
4) Обыкновенные (коммерческие) проценты с приближенным числом дней финансовой операции, иначе «360/360».
Из наиболее часто встречаемые в финансовой практике:
- «360/365» (Бельгия, Франция);
- «360/360» (Германия, Дания, Швеция);
- «365/365» (Великобритания, США, Россия).
Практически не встречается на практике расчет «365/360».
Для удобства расчета рекомендуется использовать Приложение 2.
Пример. Банк предоставляет на условиях платности, срочности, возвратности денежные средства в размере 800 тыс. руб. Срок выдачи кредита 15 апреля с погашением 22 ноября под 19% годовых (год 2011). Рассчитать различными способами сумму к погашению (FV)? Обоснуйте, почему расчет «365/360» практически не встречается на практике?
Решение.
Точное число дней финансовой операции составляет 221 день.
Приближенное число дней финансовой операции (15 дней в апреле +30*6+21 день в ноябре + 1граничный день)= 217 дней.
Возможные варианты расчета суммы к погашению на основании формулы (11):
а) точные проценты (365 или 366) с точным числом дней финансовой операции «365/365»:
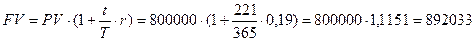руб.;
б) точные проценты с приближенным числом дней финансовой операции, «365/360»:
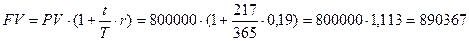руб.;
в) обыкновенные (коммерческие) проценты с точным числом дней финансовой операции, «360/365»:
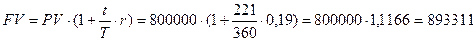руб.;
г) обыкновенные (коммерческие) проценты с приближенным числом дней финансовой операции, «360/360»:
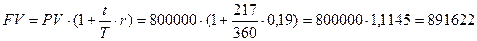руб.
Как видно из решения, максимальное наращение стоимости дает расчет обыкновенные (коммерческие) проценты с точным числом дней финансовой операции («360/365»), в то же время, минимальный - точные проценты с приближенным числом дней финансовой операции («365/360»), что и объясняет невостребованность последнего в практических финансовых расчетах.
Методические указания. Методика определение наращенной стоимости через учетную ставку распространена при учете векселей. Модифицируем формулу (8) с учетом данных о продолжительности финансовой операции:
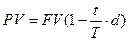, (12)
где FV – номинальная величина векселя;
PV – сумма к погашению при учете векселя;
t – число дней до погашения векселя с момента учета векселя;
T – число дней в году.
Дисконтирование по формуле (12) называют банковским дисконтирование.
Пример. Векселедержатель предъявил вексель 4 сентября 2011 года на сумму 100 000 руб. Вексель выпущен 14 марта 2011 года со сроком погашения 14 декабря 2011 года. Учетная ставка банка 19%. Определите сумму, которую векселедержатель получит от банка?
Решение.Определим сумму к получению на основании формулы (11):
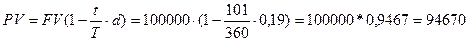руб.
Комиссионные банка за досрочный учет векселя составили 5 330 руб.
Методические указания. В практике финансовых расчетов начисление процентов производится несколько раз за период финансовой операции. В этом случае используют формулу внутригодового начисления процентов:
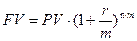, (13)
где m - количество начислений в год.
Пример. На депозит банка инвестор вкладывает денежные средства в размере 680 000 руб.
на срок 3 года. Банк предлагает следующие депозиты:
1) Депозит «12 месяцев»: процентная ставка 8,25%, начисление процентов ежемесячное;
2) Депозит «Ежеквартальный»: процентная ставка 8,25%, начисление процентов – ежеквартальное;
3) Депозит «Полгода»: процентная ставка 8,25%, начисление процентов раз в полгода;
4) Депозит «Годовой»: процентная ставка 8,25%, начисление процентов 1 раз в год.
Какой депозит выберет инвестор (FV)?
Решение. Воспользуемся формулой (13):
1) Депозит «12 месяцев»:
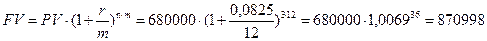руб.;
2) Депозит «Ежеквартальный»:
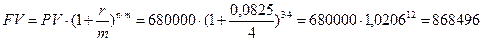руб.;
3) Депозит «Полгода»:
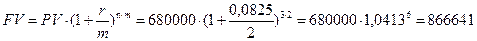руб.;
4) Депозит «Годовой»:
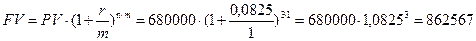руб.
Инвестор выберет депозит «12 месяцев».
Методические указания. На практике встречаются финансовые инструменты, срок которых отличается от целого числа лет (начисление процентов за дробное число лет).
Для указанных инструментов используют две способа расчета:
1) по схеме сложных процентов:
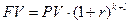, (14)
где k – целое число лет финансового инструмента;
l – дробная часть года;
n – общая продолжительность финансового инструмента,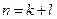 
.
Если начисление процентов осуществляется по внутригодовым периодам, а продолжительность общего периода действия финансового инструмента не равна целому числу внутригодовых периодов, то используется формула (15):
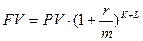, (15)
где К – число периодов m;
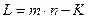
2) по смешанной форме:
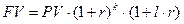(16)
Если начисление процентов осуществляется по внутригодовым периодам, а продолжительность общего периода действия финансового инструмента не равна целому числу внутригодовых периодов, то используется формула 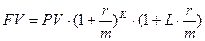(17):
(17)
Пример.
Заемщик взял в банке кредит в размере 500 000 руб. на 21 месяц под 17% годовых на условиях:
а) ежегодного начисления процентов;
б) начисления процентов раз в полгода.
Какую сумму необходимо вернуть кредитору (FV)?
Решение. 21 месяц – это 1 год и 9 месяцев (0,75 года).
а) ежегодного начисления процентов.
По схеме сложных процентов (14):
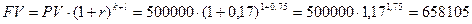руб.
По смешенной формуле (16):
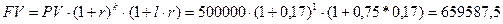руб.
Как видно из приведенного примера, наращенная сумма всегда большая при смешанной схеме начисления процентов.
б) начисление процентов раз в полгода.
Число полугодовых начислений на 1,75 года составит К=3, тогда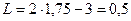 
.
По схеме сложных процентов (15):
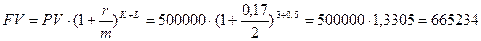руб.
По смешенной формуле (17):
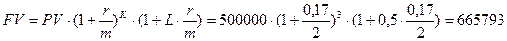руб.
Методические указания. Представленные выше проценты называются дискретными, так как их начисление осуществлялось за определенный (фиксированный) период времени. Уменьшая период времени и увеличивая частоту начисления процентов (m→∞), можно прийти к непрерывному начислению процентов.
Тогда величина наращения будет определяться по формуле:
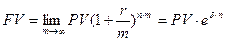, (18)
где δ - непрерывная ставка процента, или сила роста;
e – трансцендентное число (число Эйлера), е≈2,718281.
Связь дискретной ставки r с силой роста δ находится по следующей формуле:
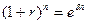(18 а)
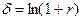(18б)
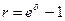(18в)
Пример. Необходимо определить накопленную сумму для различных вариантов начисления процентов за один год, если исходная сумма 100 000 руб., ставка процента 15% годовых.
Решение. Для расчета внутригодовых исчислений используем формулу (13):
- начисление 1 раз в год:
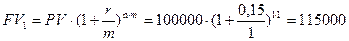руб.;
- начисление 2 раза в год:
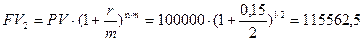руб.;
- начисление каждый квартал:
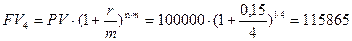руб.;
- начисление процентов ежемесячное:
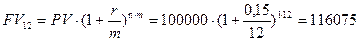руб.;
Бесконечное начисление, используем формулу (18):
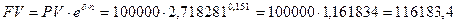руб.
Методические указания. Номинальная процентная ставка не отражает реальной эффективности финансовой операции и не может быть использована для сопоставления финансовых инструментов. Нивелировать указанные недостатки позволяет эффективная годовая процентная ставка:
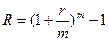(19)
Из формулы (19) следует, что для каждой номинальной процентной ставки можно найти эффективную, причем с увеличением количества начислений m, она увеличивается. Именно ставка R является критерием эффективности финансовой операции и может использоваться для пространственно-временных сопоставлений.
Пример. Инвестор рассматривает два варианта финансирования инвестиционного проекта: а) ежеквартальное начисление процентов по ставке 16% годовых; б) ежемесячного начисления процентов по ставке 14% годовых.
Решение. Относительные расходы инвестора на обслуживание кредита могут быть сопоставлены по эффективной процентной ставке:
а) ежеквартальное начисление процентов по ставке 16% годовых:
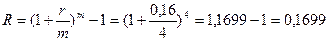или 16,99%;
б) ежемесячного начисления процентов по ставке 14% годовых:
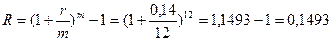или 14,93%.
Таким образом, вариант б) является более предпочтительным для инвестора.