Вопрос 2. Нелинейная регрессия. Классы нелинейных регрессий
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы, параболы второй степени и др.
Различают два класса нелинейных регрессий:
§ регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
§ регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:
§ полиномы(многочлен) разных степеней:
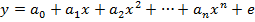
§ равносторонняя гипербола:
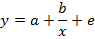
К нелинейным регрессиям по оцениваемым параметрам относятся функции:
§ степенная:
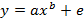
§ показательная:
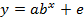
§ экспоненциальная:
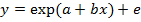
*Экспоненциальный рост — возрастание величины, когда скорость роста пропорциональна значению самой величины. Говорят, что такой рост подчиняется экспоненциальному закону*
Параметры нелинейной регрессии по включенным переменным оцениваются, как и в линейной регрессии, методом наименьших квадратов, поскольку эти функции линейны по параметрам.
Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени; в отдельных случаях – полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.
Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: приравниваем к нулю первую производную параболы второй степени. Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.
Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу:
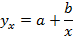
Иначе обстоит дело с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях широко используется степенная функция:
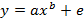
Данная модель нелинейна относительно оцениваемых параметров, ибо включает параметры 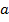 и
и 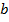 неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду. Соответственно оценки параметров
неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду. Соответственно оценки параметров 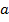 и
и 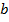 могут быть найдены с помощью МНК.
могут быть найдены с помощью МНК.
В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят, например, экспоненциальную модель 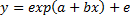 , поскольку логарифмируя ее по натуральному основанию, получим линейную форму модели:
, поскольку логарифмируя ее по натуральному основанию, получим линейную форму модели: 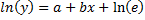 .
.
Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.
