Анализ на основе дерева решений

Анализ безубыточного объема

Постоянные затраты (Спост), тыс.ДЕ	Изделия	Переменные затраты Спер, тыс.ДЕ/шт.	Цена изделия, тыс.ДЕ/шт	Объемы продаж по периодам, тыс.ДЕ	Коэффициенты распределения постоянных затрат

	А						0,3
Б						0,4
В						0,3

1.1Норма маржинальной прибыли по изделиям:

Анализ на основе дерева решений - student2.ru

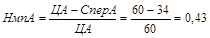
НмпБ =0,52;

НмпВ=0,48.

1.3. Распределяем сумму постоянных затрат:

СпостА=8400*0,3=2520 тыс.ДЕ.

СпостБ=8400*0,4=3360 тыс.ДЕ;

СпостВ=8400*0,3=2520 тыс.ДЕ.

Определяем объем выручки, при котором достигается точка безубыточности по каждому изделию в стоимостном и натуральном выражении:

QpбезА= (СпостА+А)/НмдА =

2520/0,43=5860 тыс.ДЕ; NбезА= QpбезА/ЦА= 5860/60=98(шт);

QpбезБ = 6462 тыс.ДЕ; NбезБ = 64 (шт);

QpбезВ= 5250 тыс.ДЕ. NбезВ = 38 (шт).

1. Предполагаем, что мощность предприятия позволяет увеличить объемы производства указанной продукции, а на рынке существует устойчивый спрос на данные изделия. Определим прибыль предприятия при объеме производства в 1,5 раза превышающем точку безубыточности по каждому изделию.

2.1. Объем продаж по изделиям:

QpА= 5860*1,5=8790 тыс.ДЕ

QpБ= 6462*1,5=9693 тыс.ДЕ

QpВ= 5250*1,5=7875 тыс.ДЕ

Суммарная выручка составит: 26358 ДЕ

2.2. Маржинальная прибыль по изделиям:

МпА = 8790*0,43=3780 ДЕ

МпБ=9693*0,52=5020 ДЕ

МпВ= 7875*0,48=3780 ДЕ

Суммарная прибыль составит: 12580 тыс. ДЕ

2.2. Определяем прибыль по изделиям:

Пi=Мпi-Спостi

ПА= 3780-2520=1260 тыс.ДЕ

ПБ=5020-3360=1680 тыс.ДЕ

ПВ= 3780-2520=1260 тыс.ДЕ

Наиболее прибыльным является изделие Б

2.4. Прибыль от реализации объема в 1,5 раза превышающем безубыточный составит:

П = Па + Пб + Пв = 4200 тыс.(ДЕ)

3.При постоянной норме маржинальной прибыли (например, Нмп= 0,5) объем выручки для достижения безубыточности составит:

Qбезуб= (Спост+А)/Нмп= 8400/0,5=16800тыс. ДЕ

3.1.Выручка при возросшем объеме производства:

Qп=16800*1,5=25200 тыс. ДЕ

Общая сумма маржинальной прибыли

МП=Qр*Нмп=25200*0,5=12600 тыс. ДЕ

3.3. Часть маржинальной прибыли пойдет на покрытие постоянных расходов и остаток прибыли составит:

П = 12600 – 8400= 4200 тыс. ДЕ

Принятие решения о целесообразности снижения отпускной изделия, переменных и постоянных затратахТаблица 2.3. Экономические показатели изделия

Показатели	Единица измерения	Условное обозначение	Значение показателя

1. Объем реализации изделия за период	ед.	N	10 000
2. Возможная цена реализации изделия	тыс.руб./ед.	Ц	48,0
3. Полная себестоимость изделия	тыс. руб./ед.	С	35,6
4. Переменные затраты в себестоимости единицы изделия	тыс.руб./ед.	Спер	14,95
5. Постоянные затраты предприятия за период	тыс.руб	Спост	206 480

Решение

1. Цена реализации изделия с учетом возможного ее снижения составит:

Ц'д = Цд - 2,8 = 48,0 - 2,8 = 45,2 ( тыс.руб.)

Планируемый объем продаж изделия по сниженной цене:

Nд = Nд (1 + 18/100)= 10000* 1,18= 11 800(ед.)

Таблица 2.4. Расчет прибыли при использовании метода калькулирования полной себестоимости

Показатели	Условное обозначение	Значение показателя при объеме продаж изделия, ед.	Изменение показателя (+.-)

1. Отпускная цена изделия, тыс.руб./ед.	Цд	48,0	45,2	-2,8
2. Полная себестоимости изделия, тыс. руб./ед.	Сд	35,6	35,6
3. Прибыль от продаж изделия, тыс. руб./ед.	Пд	12,4	9,6	-2,8
4. Прибыль предприятия от продаж всего объема , тыс. руб.	∑Пд	124 000	113 280	-10720

Таблица 2.5 Расчет прибыли при использовании метода калькулирования усеченной (неполной) себестоимости

Показатели	Условное обозначение	Значение показателя при объеме продаж изделия, шт.	Изменение показателя, (+.-)
		10 000
1. Отпуская цена изделия, тыс.руб.	Цл	48,0	45,2	-2,8
2. Переменные затраты в себестоимости изделия тыс. руб.	СперД	14,95	14,95	0,0
3. Норма маржинальной прибыли с переменной себестоимости изделия тыс., руб.	МДд	33,05	30,25	-2,5
4. Годовой маржинальный доход от продажи изделия тыс. руб.	МДд	330 500	356 950	+26 450
5. Постоянные затраты предприятия за год, тыс.руб.	Спост	206 480	206 480	0,0
6. Прибыль предприятия от реализации изделия тыс., руб. (стр.4 - стр.5)	Пд	124 020	150 470	+26 450

Таблица 2.6 Анализ влияния переменных затрат на эффект производственного левериджа

Показатели	Фактичес- кое значение	При снижении переменных затрат на 10%
Условное значение	Изменение от фактического
(+\-)	%
1.Объем продаж, тыс.руб
2.Переменные затраты, тыс. руб
3.Маржинальный доход, тыс.руб. (п. 1 - п. 2)
4.Постоянные затраты, тыс.руб.	206 480
5.Опеационная прибыль, тыс.руб. (п.3 - п.4)
6.Объем продаж, шт.
7.Цена за единицу, тыс.руб.	48,0
8.Точка безубыточности, шт.(п.4 * п.6 / (п.1 - п.2))
9. Пороговый объем продаж, тыс.руб. (п.7*п.8)
10.Маржинальный доход в расчете на единицу товара, тыс.руб. (п.3/п.6)	33,05
11. Маржинальный запас прочности ((п.6 - п.8)/ п.6)*100%	37,53
12. Эффект производственного левериджа (п.3/п.5)	2,67

Таблица 2.7.Анализ влияния постоянных затрат на эффект производственного левериджа

Показатели	Фактичес- кое значение	При снижении постоянных затрат на 10%
Условное значение	Изменение от фактического
(+\-)	%
1.Объем продаж, тыс.руб.
2.Переменные затраты, тыс.руб.
3.Маржинальный доход, тыс.руб. (п. 1 - п. 2)
4.Постоянные затраты, тыс.руб.
5.Прибыль, тыс.руб. (п.3 - п.4)
6.Объем продаж, шт.
7.Цена за единицу, тыс.руб.
8.Точка безубыточности, шт.(п.4 * п.6 / (п.1 - п.2))
9. Пороговый объем продаж, тыс.руб. (п.7*п.8)
10.Маржинальный доход в расчете на единицу товара, тыс.руб. (п.3/п.6)
11. Маржинальный запас прочности ((п.6 - п.8)/ п.6)*100%
12. Эффект производственного левериджа (п.3/п.5)

Пример 1. Предприятие планирует три стратегии производства продукции:

а)S1— выпустить на рынок новую продукцию с более высокими качественными показателями (по сравнению с существующей);

б) S2 — модернизировать существующую продукцию;

в) S3 — сохранить существующую продукцию.

Выбор решения зависит от экономической ситуации в стране. Рассматриваются два варианта объективных условий:

1) У1 — экономическая ситуация в стране улучшится;

2) У2 — экономическая ситуация в стране ухудшится. Предполагаемая прибыль от реализации продукции приведена в табл. 4.2.

Таблица 4.2 Матрица возможных результатов (прибыли), млн. руб.

	У1	У2
S1
S2
S3

Определите, какую стратегию выбрать предприятию при условии:

1. Руководство предприятия уверено, что экономическая ситуация в стране улучшится (выбор в условиях достоверности).

2. Руководство оценивает вероятность улучшения экономической ситуации в 0,6 (выбор в условиях риска).

3. В условиях риска оценить оптимальные границы реализации каждой стратегии.

Рекомендации к решению:

1. Если руководство предприятия уверено в том, что экономическая ситуация в стране станет лучше (т. е. У1), то среди стратегий выбирается та, которая обеспечивает получение максимальной прибыли от реализации продукции, т. е. стратегия S1, (выпустить новую продукцию) с результатом 18 млн. руб.

2. Внесем вероятности возникновения объективных условий в матрицу результатов и подсчитаем математическое ожидание прибыли по каждой стратегии (табл. 4.3).

Таблица 4.3 Матрица результатов (ожидаемой прибыли)

	У1	У2	Расчет математического ожидания прибыли
S1			18 0,6 + 2 0,4=11,6
S2			15 0,6 +9-0,4= 12,2
S3			8 0,6+ 16 0,4 = 11,2
Вероятность	0,6	0,4

Получение максимального результата обеспечивает стратегия S2, т. е. необходимо модернизировать существующую на предприятии продукцию.

3. Как установлено выше, выбор в условиях риска зависит от точности оценки вероятности возникновения объективных условий. Определим оптимальные границы реализации каждой стратегии, т. е. рассчитаем вероятности, при которых каждая стратегия обеспечивает наилучший результат. Для этого воспользуемся графическим методом (рис. 4.1). На левой стороне графика представлена прибыль, которую может получить предприятие, если вероятность возникновения условий У1, равна 100%, на правой стороне — прибыль предприятия при условии

Анализ на основе дерева решений - student2.ru

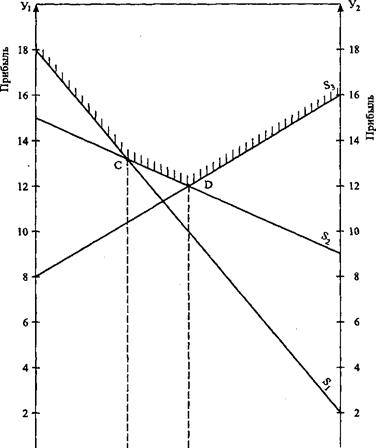
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 р(У₂)

Рис. 4.1. Оптимальные границы реализации стратегий

что вероятность У1, равна 0%. Следует учитывать и тот факт, что условия У1 и У2 взаимоисключающие, т. е. р(У1) + р(У2) = I.

Прямой линией на графике показана величина прибыли по Si стратегии при различных значениях р(У1). Оптимальной будет стратегия, имеющая наиболее высокое значение прибыли — при данном значении вероятности р(У1).

Для получения координат точек пересечения стратегий между собой необходимо представить каждую стратегию уравнением прямой вида

S i= Аi + ВiХi,

где Д—точка пересечения стратегии Si с осью У1; Вi — угол наклона прямой Si к горизонтальной оси р(У₂); Xi — вероятность стратегии У₂, т. е. р(У₂).

В силу того, что расстояние между осью У1 и У₂ равно 1, наклон прямой равен разнице в величине прибыли на оси У₂ и прибыли на оси У1,т. е.

S₁= 18 + (2 - 18) • р(У₂) = 18 - 16 • р(У₂);

S₂ = 15 + (9 - 15) • р(У₂) = 15 - 6 • р(У₂);

S₃ = 8 + (16 - 8) • р(У₂) = 8 + 8 • р(У₂).

На рис. 4.1 видно, что стратегия S1, является оптимальной (приносит высокую прибыль) от р(У₂) = 0 до точки пересечения S1 и S₂ (точка С), стратегия S₂ является лучшей от точки С до точки D и, начиная от точки D до р(У₂) = 1, наиболее выгодной является стратегия S₃.

В точке С имеем S1 = S₂, т. е. 18 - 16 • р(У₂) = 15 - 6 • р(У₂), откуда р(У₂) = 0,3, т. е. стратегия S1 будет оптимальной в диапазоне р(У₂) = 0 до р(У₂) = 0,3.

Точка D — это точка пересечения S₂ и S₃, т. е. 15 - 6 • р(У₂) = 8 + 8 • р(У₂) и р(У₂) ⁼ =0,5. Следовательно, стратегия S₂ будет лучшей в диапазоне от р(У₂) = 0,3 до р(У₂) = 0,5 и стратегия S₃ будет оптимальной от р(У₂) = 0,5 до р(У₂)=1.

Существует два способа определить значение EVPI (expected value of perfect information):

Пример 2. Руководство предприятия не в состоянии оценить вероятность появления объективных условий. Используя информацию табл. 4.4, необходимо выбрать разумное решение по каждому из следующих критериев:

1) критерий максимин;

2) критерий максимакс;

3) критерий минимизации сожалений по упущенным возможностям;

4) критерий недостаточного основания(Лапласа).

5) критерий Гурвица

6) критерий предполагаемой стоимости точной информации

7) критерий предполагаемой денежной стоимости (EMV) - решение в условиях риска

8) провести анализ на основе дерева решения

Рекомендации к решению:

1. Выбор по критерию максимина (Вальда) (табл. 4.4).

Таблица 4.4. Матрица результатов (предполагаемой чистой прибыли)

	У1	У2	Мin, (млн.руб)
S1
S2
S3

Максимальное значение прибыли из наихудших обеспечивает S2, она и принимается к реализации.

2. Критерий максимакса (табл. 4.5).

Таблица 4.5. Матрица результатов

	У1	У2	Мах,млн.руб
S1
S2
S3

Наилучшим результатом является 18 млн. руб., т. е. выбирается стратегия S1.

3. Критерий минимизации сожалений (табл. 4.6).

Таблица 4.6. Таблица «сожалений»minimax regret

	У1	У2	Наихудший вариант
S1
S2
S3

Лучшим из наихудших значений является стратегия S2. Именно она обеспечивает наименьшие сожаления по упущенным возможностям.

4. Критерий недостаточного основания (критерий Лапласа).

Вследствие того, что рассматриваются два варианта объективных условий, вероятность их появления принимается по 0,5, и выбор решения приведен в табл. 4.7.

Таблица 4.7. Матрица результатов

	У1	У2	Математическое ожидание
S1
S2
S3
Вероятность	0,5	0,5

Согласно данному критерию, можно принять к реализации либо стратегию S2, либо S3. Они равноэффективны.

Необходимо отметить, что все перечисленные критерии разумны, и выбор решения зависит от системы ценностей, положенных в основу выбора. Так, если руководитель осторожен и по природе пессимист, то, скорее всего за критерий будет принят максимин или критерий Сэведжа.

5. Критерий Гурвица. Зададим а - 0,4 и b — 0,6. а + b = 0,4 + 0,6 = 1. Из таблицы возможных доходов для каждого решения находим наименьший и наибольший возможные доходы (это числа в строках «максимакс» и «максимин»)- Заполним таблицу 4.8.

Числа во 2-м и 3-м столбцах взяты из таблицы возможных доходов. Числа 3-го столбца умножаем на а — 0,4 и результат пишем в 4-м столице, числа 3-го столица умножаем на b — 0,6 и результат пишем в 5-м столбце. В 6-м столбце находится сумма соответствующих элементов 4-го и 5-го столбцов. Находим максимум в 6-м столбце (это11,4). Он соответствует возможному решению о реализации стратегии S2. Очевидно, для других весов результат будет, вообще говоря, иным.

В методе Гурвица вместо таблицы возможных доходов можно воспользоваться таблицей возможных потерь. В этом случае ищется максимум целевой функции ах (наименьшие потери) + bх(наибольшие потери) по всем возможным решениям.

Таблица 4.8. Матрица результатов(доходов)

	Наибольший доход	Наименьший доход	a*(наибольший доход)	b*(наименьший доход)	Сумма

S1			7,2	1,2	8,4
S2				5,4	11,4 - max
S3			6,4	4,8	11,2
Вероятность	0,4	0,6	-	-

6.Максимизация ожидаемого дохода (EMV)

Таблица 4.9.

	У1	У2	EMV-максимизация ожидаемого дохода
S1
S2
S3
maximax(р)	18*0,4=7,2	16*0,6=9,6	EMV= 7,2+9,6=16,8

7. Предполагаемая стоимость точной информации

EVPI = предполагаемая стоимость в условиях уверенности(EMV) - предполагаемая прибыль в условиях риска

Таблица 4.10 Расчет EVPI на основе ожидаемой прибыли в условиях уверенности и риска

	У1	У2	EMV	математическое ожидание в условиях риска
S1			7,2+9,6=16,8	180,4+20,6=8,4
S2			150,4+90,6=9,6
S3			80,4+160,6=12,8
maximax(p)	18*0,4=7,2	16*0,6=9,6
EVPI	16,8-12,8=4 (min)

Таблица 4.11 РасчетEVPI на основе матрицы сожалений

	У1	У2	Математическое ожидание
S1			00,4+140,6=8,4
S2			30,4+70,6=5,4
S3			100,4+00,6=4
EVPI	4 (min)****- наименьший убыток

Анализ на основе дерева решений

Пример 3. Для финансирования проекта бизнесмену нужно занять сроком на один год 15000 $. Банк может одолжить ему эти деньги под 15% годовых или вложить в дело со 100 %-ным возвратом суммы, но под 9% годовых. Из прошлого опыта банкиру известно, что 4% таких клиентов ссуду не возвращают. Что делать? Давать ему заем или нет? Перед вами пример задачи с одним решением, поэтому можно воспользоваться как таблицей доходов, так и "деревом". Рассмотрим оба варианта. Рекомендации к решению (по таблице доходов). Максимизируем ожидаемый в конце года чистый доход, который представляет собой разность суммы, полученной в конце года, и инвестированной в его начале. Таким образом, если заем был выдан и возвращен, то чистый доход составит:

Чистый доход = ((15000 + 15% * 15000) - 15000) = 2250 $

Таблица 4.12 . Чистый доход в конце года, $

Возможные исходы	Возможные решения	Вероят- ность
Выдавать заем	не выдавать заем
Клиент заем возвращает			0,96
Клиент заем не возвращает	-15000		0,04
Ожидаемый чистый доход